Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Автоматизированное проектирование технических систем: Учебное пособие.

Бельков В. Н., Ланшаков В. Л.,

3.1.3. Кольцевая колонна

Колонна, имеющая поперечное сечение в виде кольца, должна выдерживать заданную нагрузку P. Целью оптимизации является определение радиуса колонны R и ее толщины t, которые минимизируют вес колонны при ограничении на напряжение и эйлерову силу потери устойчивости, а также при ограничениях на местное выпучивание. В предположении t<<R геометрические характеристики сечения таковы: S=2πRt и I= πR³t. Эйлерова критическая сила потери устойчивости находится по формуле:

.

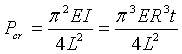Осевое напряжение определяется выражением:

σс=P/S=P/(2πRt).

Осевое критическое напряжение потери устойчивости в стальной цилиндрической оболочке равно σсг=kEt/R, где k-коэффициент, для стали приближенно равный 0.6. Ограничение на местную потерю устойчивости записывается в виде неравенства σс<σсг  или:

P - 2πkEt²<0.

Анализ выполнить при следующих исходных данных: [σc]=2·10⁸ Па; k=0.6;

E=2·10¹¹ Па; ρ=7800 кг/м³; L=0.5 м; P=10 000 Н.

Для решения данной задачи оптимального проектирования воспользуемся методом Куна-Таккера.

Запишем целевую функцию; по условию задачи ей является вес:

f(x)=G(R,t)=ρgSL=ρg2πRtL.                                                              (1)

Ограничение на напряжение имеет вид:

g1(x)=σc<[σc] или g1(x)=P/S-[σc]=P/(2πRt)- [σc]<0,

иначе можно записать:

g1(x)=P-[σc]S=P- [σc]2πRt <0.                                                           (2)

Ограничение на эйлерову силу потери устойчивости определяется из выражения:

g2(x)=P<Pcr или g2(x)=P-π³ER³t/(4L²)<0.                                       (3)

Ограничение на местную потерю устойчивости (местное выпучивание) находится по формуле:

g3(x)=P-2πkEt²<0.                                                                              (4)

Следовательно, функция Лагранжа имеет вид:

L=f(x)+Σνigi=ρg2πRtL+ν1(P-[σc]2πRt)+ ν2(P- π³ER³t/(4L²))+ ν3(P-2πkEt²)  (5)

Определяем частные производные функции Лагранжа по каждому из аргументов:

¶L/¶R=Ρg2πtL - ν1[σc]2πt - ν2 3π³ER²t/(4L²);

¶L/¶t=ρg2πRL+ν1[σc]2πR+ ν2 π³ER³/(4L²)+ ν34πkEt.

Составляем систему уравнений, которая включает в себя определенные выше частные производные и заданные ограничения, подставляя численные значение известных параметров:

¶L/¶R =240304t-1.257·10⁹ ν1t - 1.86·10¹³ ν2 R²t=0;

¶L/¶t =240304R - 1.257·10⁹ ν1R - 6.201·10¹² ν2 R³ -1.508·10¹² ν3t =0;

ν1(10000-1.257·10⁹ Rt)=0;

               ν2(10000- 6.201·10¹² R³t)=0;         (6)

ν3(10000-7.54·10¹¹t²)=0.

Решением системы уравнений (6) являются искомые значения переменных R и t, которые минимизируют общий вес колонны. Проанализируем равенство нулю каждого из сомножителей последних трех уравнений.

При этом возможны следующие 8 вариантов.

• 1) ν1>0, ν2>0,ν3>0; g1(x)=0, g2(x)=0, g3(x)=0;

отсюда следует, что t=0.000115 м, тогда R=0.069 м, но при этом g2(x)=-224274,

следовательно, в этом случае нет решения.

• 2) ν1>0, ν2>0,ν3>0; g1(x)<0, g2(x)=0, g3(x)=0;

аналогично предыдущему случаю t=0.0.000115 м, R=0.024 м.

Подставив эти значения в первое уравнение системы (6), получим:

ν2=0.00002243, а из второго уравнения следует, что ν3=0.00002213; все множители Лагранжа неотрицательны, но g1(x)=6526>0, следовательно, и этот вариант решением не является.

• 3) ν1>0, ν2=0,ν3>0; g1(x)=0, g2(x)<0, g3(x)=0;

так как g3(x)=0, то t=0.000115 м, а при g1(x)=0 R=0.069 м;

из первого уравнения системы (6) находим ν1=0.0001912, из второго ν3=0; g2(x)=-224682<0, следовательно, полученные значения R и t являются решением задачи.

• 4) ν1>0, ν2>0,ν3=0; g1(x)=0, g2(x)=0, g3(x)<0;

решая совместно уравнения g1(x)=0 и g2(x)=0, находим из системы R=0.014 м и t=0.00056 м; подставляя эти значения в первые два уравнения системы находим ν1=0.0001912 и ν2=0; проверим третье ограничение: g3(x)=-225605<0, значит, получено верное решение.

• 5) ν1=0, ν2=0,ν3>0; g1(x)<0, g2(x)<0, g3(x)=0;

из последнего условия получаем t=0.000115 м, но тогда ¶L/¶R=27,683>0, поэтому в данном случае решения нет.

• 6) ν1=0, ν2>0,ν3=0; g1(x)<0, g2(x)=0, g3(x)<0;

из системы уравнений (6):

¶L/¶R=240304t-1.86·10¹³ ν2 R²t=0, откуда ν2=240304/(1.86·10¹³ R²) >0;

¶L/¶t=240304R-6.201·10¹² ν2 R³ =0, откуда ν2=240304/ (6.201·10¹² R²)>0;

очевидно, что полученные из разных уравнений значения ν2 неодинаковы, поэтому в данном случае решения нет.

• 7) ν1>0, ν2=0,ν3=0; g1(x)=0, g2(x)<0, g3(x)<0;

из первого уравнения системы (6) следует, что ν2=240304/1.257·10>0; второе уравнение дает аналогичный результат.

Значения R и t находятся из уравнения:

g1(x)=10000 - 1.257·10⁹ Rt=0;

следовательно, из этого уравнения можно получить зависимость:

t(R)=10000/(1.257·10⁹ R).                                                                           (7)

Подставляя эту зависимость в ограничение (3) получаем:

10000- 6.201·10¹² R³(10000/(1.257·10⁹ R))<0,

откуда находим, что R>0.014 м; а, подставляя зависимость (7) в выражение (4) получим R<0.069 м; таким образом, допустимые значения R лежат в диапазоне  от R=0.014 м до R=0.069 м, а соответствующие им значения t - в диапазоне от t=0.000115 м до t=0.000559 м.

• 8) ν1=0, ν2=0,ν3=0; g1(x)<0, g2(x)<0, g3(x)<0;

в этом случае: ¶L/¶R =240304t≠0 и ¶L/¶t=240304R ≠0, поэтому оптимального решения не существует.

Проанализировав все 8 вариантов можно сделать вывод, что колонна имеет минимальный вес, когда ее размеры R и t, связанные зависимостью (7), лежат в диапазонах R≥0.014 м, R≤0.069 м, t≥0.000115 м и t≤0.000559 м.