
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

Автоматизированное проектирование технических систем: Учебное пособие.
Бельков В. Н., Ланшаков В. Л.,
3.1.4. Двутавровая балка
Стальная призматическая балка с горизонтальной осью симметрии проектируется на сосредоточенную нагрузку.
Балка должна иметь минимальный вес при ограничениях на изгибающие ограничения в полках и на местную потерю устойчивости полок и стенки. Из четырёх переменных, определяющих форму поперечного сечения, в качестве переменных проектирования выбираются переменные высота h и ширина t, а толщины стенок (соответственно горизонтальная k1 и вертикальная k2) считаются заданными.
Ограничение на напряжение задаётся неравенством:
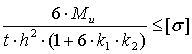 ,
,
где Ми - изгибающий момент.
Выражение для критического напряжения при выпучивании σLимеет вид: 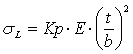 ,
,
где Kp - коэффициент выпучивания: для полок Кр = 0,385, для стенки Кр = 3,62.
Ограничения на местную потерю устойчивости находятся из выражений:
- - для полок:
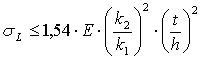 ,
, - - для стенки:
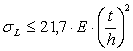 .
.
Используя обозначения: 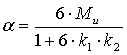 ,
, ![]() ,
,
![]() ,
, 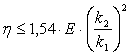 ,
,
определить оптимальное решение.
Для решения этой задачи используем метод Куна - Таккера. ЦФ имеет вид:
f(h,t) = ρlS = ρl(2k1k2th)+ ρlht = ρlβht = Aht,
где A=ρlβ.
В данном случае ограничения находятся из выражений:
•(1) g1(h,t)=α/(ht²)-KpE(t/b)²;
•(2) g2(h,t)=α/(ht²)-1.54(k2/k1) ²(t/h)²=α/(ht²)-η(t/h)²;
•(3) g3(h,t)=α/(ht²)-21.7E(t/h)²=α/(ht²)-ν(t/h)².
Функция Лагранжа записывается в виде:
L=Aht-ν1(α/(htІ)- KpE(t/b)І)-ν2(α/(htІ)-η(t/h)І)-ν3(α/(htІ)-ν(t/h)І).
•(4) ¶L/¶h=At+ ν1α/tІhІ+ ν2(α/(hІtІ)-ηtІ/hі)+ν3(α/(hІtІ)-νtІ/hі);
- (5) ¶L/¶t= Ah+ν1α/tіh+ ν2(α/(htі)-ηt/hІ)+ν3(α/(htі)-νt/hІ).
Проанализируем все возможные сочетания, которые могут иметь место при равенстве нулю одного из сомножителей.
•1. ν1>0,ν2>0, ν3>0; g1=0, g2=0, g3=0.
•2. ν1=0,ν2>0, ν3>0; g2=0, g3=0.
•3. ν1>0,ν2=0, ν3>0; g1=0, g3=0.
•4. ν1>0,ν2>0, ν3=0; g1=0, g2=0.
•5. ν1=0,ν2=0, ν3>0; g3=0.
•6. ν1=0,ν2>0, ν3=0; g2=0.
•7. ν1>0,ν2=0, ν3=0; g1=0.
•8. ν1=0,ν2=0, ν3=0.
При заданных параметрах нагружения и характеристик материала анализ представленных вариантов позволяет получить оптимальное решение; при этом расчет проводится аналогично задаче 3.1.2.