Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

Автоматизированное проектирование технических систем: Учебное пособие.
Бельков В. Н., Ланшаков В. Л.,
3.1.5. Колодочный тормоз
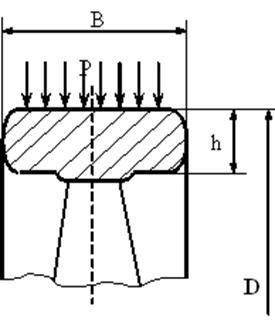
В данном расчете ЦФ является взвешенная сумма массы обода колодочного тормоза, изображенного на рис. 3.3, и термо - упругого напряжения, определяемая по формуле:
f(x)=a1prBDh+a2sjj,,
|
Рис. 3.3. Колодочный тормоз. |
где a1 и а2 - весовые коэффициенты; ρ - плотность материала обода шкива; σφφ - термоупругое напряжение обода шкива. Величина σφφ, находится из выражения:
где α - температурный коэффициент линейного расширения материала обода; Е - модуль Юнга; μ - коэффициент Пуассона; t1, t2 -температура обода шкива соответственно до и после торможения. |
Температура обода определяется из условия равенства аккумулируемой теплоты в единицу времени и мощности, затрачиваемой на преодоление сопротивления трения:
![]() ,
,
где с - удельная теплоемкость материала обода;
k - коэффициент, учитывающий долю аккумулируемой ободом энергии;
ω0 - начальная угловая скорость обода;
τ - продолжительность торможения;
mт - момент трения в конце торможения, определяемый по формуле:
![]()
где Р - давление колодок на поверхность тормозного обода;
f - коэффициент трения между поверхностями колодки и тормозного обода.
Из условия прочности на изгиб: 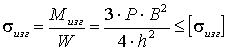
можно получить: 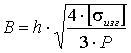 .
.
На оптимизируемые параметры накладывается ограничение - крутящий момент не превышает момента трения:
![]() .
.
Методом геометрического программирования определить параметры оптимальной конструкции тормоза: h, D и В, используя при этом указание, согласно которому модель оптимизации необходимо представить в виде:
![]()
![]()
В этих выражениях постоянные С определяются по следующим формулам:
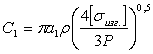 ;
;
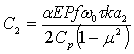 ;
;
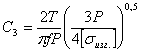 .
.
Поскольку в данной задаче степень трудности d=0, то двойственные переменные находятся из системы линейных уравнений, включающей условия нормализации и ортогональности:
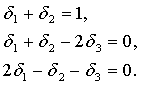
Решением данной системы являются следующие значения:
![]()
Максимум двойственной функции находится по формуле:
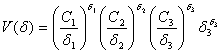 .
.
На основе выполненного анализа можно записать:
![]() .
.
Для определения оптимальных параметров тормоза используются следующие соотношения:
![]() ;
;
![]() .
.
Решая эту систему относительно D и h, можно получить:
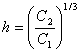 ;
; 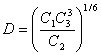 .
.
Следовательно, расчетные формулы имеют вид:
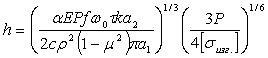 ;
;
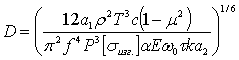 ;
;
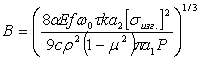 .
.
В зависимости отисходных данных, представленные анпалитические формулы позволяют рассчитать оптимальную конструкцию тормоза.