Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Автоматизированное проектирование технических систем: Учебное пособие.

Бельков В. Н., Ланшаков В. Л.,

3.1.6. Подшипник скольжения

Величина Δ находится из выражения:

где v - износ цапфы на единицу мощности, затрачиваемой на трение;

f - коэффициент трения;

F - радиальная сила, действующая на подшипник;

 - радиус подшипника;

ω- угловая скорость вала.

Коэффициент трения определяется по формуле:

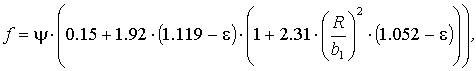
где ψ - относительный зазор;

ε - относительный эксцентриситет;

.

Прогиб вала в подшипнике находится из выражения:

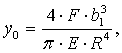
где Е - модуль продольной упругости материала вала.

На оптимизируемые параметры накладывается ограничение:

где 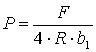 - среднее давление на подшипник;

 - допустимое давление.

Задача состоит в том, чтобы методом геометрического программирования определить параметры оптимального подшипника скольжения, приняв следующую модель оптимизации:

Степень трудности этой задачи d = 4-(2+1) = 1.

Двойственная функция V(d) = (C₁/d₁)^d1 (C₂/d₂)^d2 (C₃/d₃)^d3 C₄^d4

При двойственных ограничениях 0 £ d₁, 0 £ d₂  0 £ d₃ , 0 £ d₄  система уравнений, состоящая из условий нормализации и ортогональности, имеет вид:

d₁+d₂+d₃ = 1;

d₁+3d₂-4d₃ - d₄ = 0;

-2d₂+3d₃ -d₄ = 0.

Приняв d₃ = r, получим: d₁ = 5/4 - r; d₂ = -1/4 + 2r; d₄ = 0,5 - r.

Уравнение равновесия для данной задачи после подстановки выражений для d_i имеет вид:

4(5-12r)^-3 (8r-1)² r = C₂² C₃/ (C₁³ C₄),

где ;

;

;              .

После определения правой части уравнения по заданным исходным данным решается нелинейное уравнение относительно r , а затем вычисляются значения двойственных переменных, что позволяет найти величины оптимизируемых параметров и ЦФ.