
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

Автоматизированное проектирование технических систем: Учебное пособие.
Бельков В. Н., Ланшаков В. Л.,
3.1.7. Червячно-цилиндрический редуктор
В задаче определения оптимальных значений параметров червячно-цилиндрического редуктора в качестве ЦФ принята суммарная стоимость с материалов обеих ступеней:
![]()
где К1´- весовой коэффициент, учитывающий стоимость единицы массы червячного колеса и червяка; К2´- весовой коэффициент, учитывающий стоимость единицы массы колес цилиндрической ступени редуктора; т12 - масса червячного колеса; т21 и т22 - масса соответственно ведущего и ведомого колеса цилиндрической ступени.
В червячной ступени стоимость червяка учитывают при определении весового коэффициента червячного колеса, обод которого в большинстве случаев изготовляют из дефицитных материалов с антифрикционными свойствами.
При введении коэффициента f = К1´/ К2´ параметр К определяется по формуле:
![]()
Масса каждого колеса находится из выражения:
![]()
где n- индекс ступени; m - индекс колеса; р - плотность материала колеса; В - ширена колеса; d - диаметр делительной окружности колеса.
Конструктивные параметры определяются по формулам:
B1=ydd11 , d12=z12ms1 , z12=u1z11, d11=qms1 ,
где В1 - ширина червячного колеса; yd - коэффициент ширины; d11 - диаметр червяка; d12 - диаметр делительной окружности червячного колеса; u1 - передаточное число червячной ступени; z11 - число заходов червяка; z11 - число зубьев червячного колеса; g - относительная толщена червяка; ms1 - осевой модуль зацепления.
Обозначив: ![]() а также учитывая В2 = yaa2 и d22 = u2d21 , первое слагаемое ЦФ имеет вид:
а также учитывая В2 = yaa2 и d22 = u2d21 , первое слагаемое ЦФ имеет вид:
![]() ,
,
а сумма второго и третьего слагаемых:
![]()
где ρ1 - плотность материала колес цилиндрической ступени; yа - коэффициент ширины зуба; d21 и d22 - диаметр делительной окружности соответственно ведущего и ведомого колеса цилиндрической ступени; а2 - межосевое расстояние цилиндрической ступени; и2 - передаточное число цилиндрической ступени.
Из расчёта цилиндрической зубчатой передачи на контактную прочность можно записать:
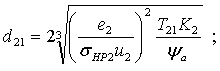
где е2 = 340·103 ![]() ; sНР2 - допустимое контактное напряжение материала зубьев шестерни цилиндрической ступени; Т21 - крутящий момент на ведущем валу цилиндрической ступени редуктора; К2 - коэффициент нагрузки.
; sНР2 - допустимое контактное напряжение материала зубьев шестерни цилиндрической ступени; Т21 - крутящий момент на ведущем валу цилиндрической ступени редуктора; К2 - коэффициент нагрузки.
Момент на ведущем валу определяется по формуле:
Т21 = и1h1Т11,
где Т11 - крутящий момент на ведущем валу редуктора; h1 - КПД первой ступени передачи.
Следовательно, сумма масс колеса и шестерни передачи находится из выражения:
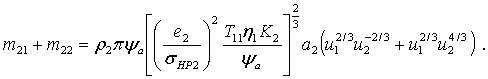
Итак, ЦФ имеет вид:
![]()
где 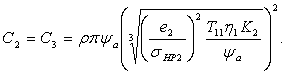
В качестве ограничений на параметры оптимизации и1, и2, t и а2 примем ограничения на контактные напряжения, возникающих в зацеплениях червячной и цилиндрической передач, и на общее передаточное число и:
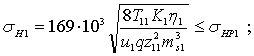
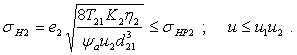
Так как d21 = 2а2/(1+ и2), то, обозначив:
![]()
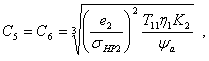 С7 = и,
С7 = и,
получим следующие нелинейные ограничения в виде неравенств:
![]()
![]()
![]()
Таким образом, задача оптимизации двухступенчатого червячно-цилиндрического редуктора сведена к решению задачи геометрического программирования со степенью трудности задачи:
d = 7 - (4 + 1) = 2.
Соответствующая этой задаче двойственная программа состоит в максимизации двойственной функции:
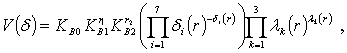
где ![]() i = 1,2, . . . , 7;
i = 1,2, . . . , 7;
![]() k = 1, 2, 3.
k = 1, 2, 3.
В этих выражениях: ![]()
Условия неотрицательности на вектор r:
![]() i = 1,2, . . . , 7.
i = 1,2, . . . , 7.
Базисные постоянные находяися из выражения:
![]() Сi > 0 - коэффициенты, зависящие от исходных данных.
Сi > 0 - коэффициенты, зависящие от исходных данных.
Вектор нормализации b(0) удовлетворяет условию соответственно нормализации и ортогональности:
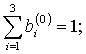
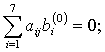 j = 1, 2, 3, 4.
j = 1, 2, 3, 4.
Векторы невязки b(j) (j = 1, 2) образуют базис пространства решений однородной линейной системы:
![]()
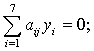 j = 1, 2, 3, 4.
j = 1, 2, 3, 4.
где аij - матрица экспонент исходной задачи геометрического программирования.
Векторы b(0), b(1) и b(2), найденные в результате преобразований матрицы экспонент по методу Бранда, имеют вид:
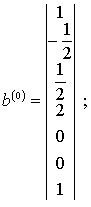
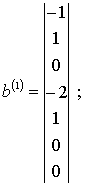
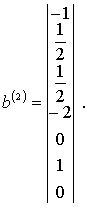
Несложно проверить, что полученные векторы нормализации и невязки удовлетворяют необходимым условиям.
Следовательно, двойственные переменные находятся по формулам:
d1 = 1 - r1 - r2;
d2 = -0,5 + r1 + 0,5r2;
d3 = 0,5 + 0,5r2;
d4 = 2 - 2r1 - 2r2;
d5 = r1;
d6 = r2; d7 = 1.
Значения r1 и r2, максимизирующие двойственную функцию, определяются из решения системы:
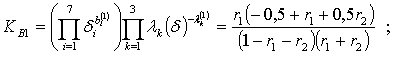
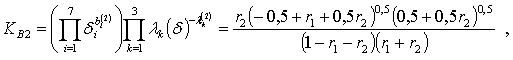
где базисные постоянные находятся по формулам:
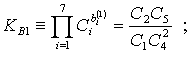
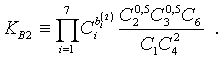
После определения максимизирующих значений r1 и r2 максимальное значение двойственной функции можно найти из выражения
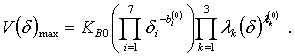
Это значение определяет одновременно и минимум ЦФ.
Оптимальные значения u1, u2, t и a2 находятся из решения системы уравнений:
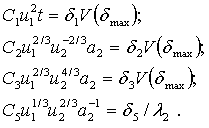
Решив эту систему, получим формулы для вычисления оптимизируемых параметров:
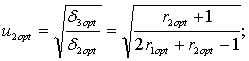
![]()
![]()
Следует отметить, что аналогичный подход можно применить для многоступенчатых редукторов и других типов, когда из рекомендуемого диапозона передаточных чисел необходимо выбрать единственное решение, минимизирующее ЦФ.