Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Автоматизированное проектирование технических систем: Учебное пособие.

Бельков В. Н., Ланшаков В. Л.,

3.2.1. Двухопорная цапфа

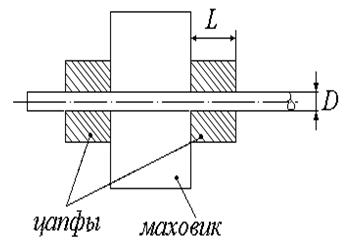
Маховик веса W, установленный на оси диаметра D. поддерживается двухопорной цапфой, изображенной на рис. 3.5. Требуется определить L и D таким образом, чтобы минимизировать момент трения вращающейся оси при допустимом зазоре на смазку.

e - эксцентриситет конструкции, определяемый как ,

где 0 < e < , а  - верхний предел эксцентриситета конструкции;

h₀ - наименьшая толщина масляного покрытия при установившемся режиме работы механизма.

Ограничения на h₀ налагаются следующими неравенствами :

        ,

где  - минимальная толщина масляного покрытия.

Угол кручения оси q должен быть не больше заданного q_мах, а его величина определяется по формуле:

,

где k₂ - константа, зависящая от точки приложения вращающего момента на оси.

Вес маховика W и нагрузки на опоры С должны быть связаны неравенством:

2С ≥ W.

Из гидродинамических соображений безопасная нагрузка на опоры определяется соотношением:

,

где  .

Таким образом, при заданных величинах q_мах найти такие параметры D, L, h₀, чтобы минимизировать момент трения. Неизвестные обозначим следующим образом: x₁ = D, x₂ = L, x₃ = h₀. Поэтому модель оптимизации имеет вид:

целевая функция - ,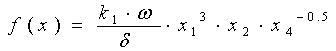

ограничения: 1) (1 - ē) δx₃^-1<1,

2) 1/(Q_maxk₂)x₁^-1<1,

3) 2/ δ x₄^-1 x₃ - 2/ δ² x₄^-1 x₃²<1,

4) 2 k₁ωπW/ δ² x₁^-1 x₂^-3 - 2 k₁ωπW / δ³ x₁^-1 x₂^-3 x₃^-1<1.

Определим степень трудности данной оптимизационной задачи:

d = n - m - 1,

где n = 7 - количество позиномов, входящих, как в целевую функцию, так и в ограничения; m = 4 - количество неизвестных; поэтому:

d = 7 -4 - 1 = 2.

Составим систему уравнений, первое из которых является условием нормализации, а остальные - ортогональности:

δ₁ = 1

3δ₁ - δ₃ - δ₆ - δ₇ = 0

δ₁ -3 δ₆ -3 δ₇ = 0

-δ₂ + δ₄ + 2 δ₅ - δ₇ = 0

-0,5 δ₁ - δ₄ - δ₅ = 0

Введем базисные переменные r₁ = δ₅, r₂ = δ₂; тогда:

δ₁ = 1

δ₂ = r₂

δ₃ = 8/3

δ₄ = -1-r₁ - r₂

δ₅ = 0,5 + r₁ + r₂

δ₆ = 1/3 - r₁

δ₇ = r₁

Решая систему нелинейных уравнений равновесия

(-1 - r₁ - r₂)^-1 r₁(-1/5 - 2r₁ -2 r₂)² (1/3 - 2 r₁)² (0,5 + r₁ + r₂) (1/3 - r₁)^-1 = 1/2δ² и

(-1 - r₁ - r₂)^-1 (-1/5 - 2r₁ -2 r₂)² (0,5 + r₁ + r₂) = (1- ē )/2, 

найдем r_1, r₂. Подставляя найденные значения базисных переменных, можно определить значения двойственных переменных, по которым определяется значение двойственной функции V(δ).

Анализ представленной ММ показывает, что данная задача относится к обобщенному математическому программированию, поэтому значение двойственной функции не является оценкой значения ЦФ. В связи с этим, решение прямой задачи заключается в поиске стационарных точек двойственной задачи.

Следует отметить, что для решения обобщенных задач геометрического программирования разработано два типа методов: последовательные методы, использующие ряд аппроксимационных задач с помощью метода конденсации, и методы непосредственного решения в одном из эквивалентных видов, к которым относятся, например, экспоненциальный и дробно - геометрический с ограничениями в виде неравенств разных знаков.
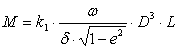