Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Автоматизированное проектирование технических систем: Учебное пособие.

Бельков В. Н., Ланшаков В. Л.,

3.2.2. Двухстержневая конструкция

В этой задаче необходимо составить математическую модель минимизации веса конструкции, представленной на рис. 3.6, и провести анализ различного случая крепления стержней в точке С.

При проектировании необходимо учитывать следующие ограничения.

• 1. Высота конструкции не должна превышать b₁.
• 2. Отношение среднего диаметра трубки к толщине её стенок не должно превышать b₂.
• 3. Прочностные соотношения для напряжений сжатия и изгиба:

Р (S² + x²₃)^1/2£ b₃  x₁  x₂  x₃

Р (S² + x²₃)^3/2£ b₄  x₁  x₂  x₃ (x²₁ + x²₂),

где b₃, b₄ - известные параметры.

• 1. x₃£ b₁
• 2. x₁x₂^-1£ b₂
• 3. Р(S² + x²₃)^1/2 x₁^-1 x₂^-1 x₃^-1£ b₃
• 4. Р(S² + x²₃)^3/2 x₁^-1 x₂^-1 x₃^-1(x²₁ + x²₂)^-1£ b_4.

В соответствии с методом геометрического программирования ограничения переписываются в следующем виде:

• 1. x₃ b₁^-1£1
• 2. x₁x₂^-1 b₂^-1£ 1
• 3. Р(S² + x²₃)^1/2 x₁^-1 x₂^-1 x₃^-1 b₃^-1£1
• 4. Р(S² + x²₃)^3/2 x₁^-1 x₂^-1 x₃^-1(x²₁ + x²₂)^-1 b₄^-1£ 1,

а также для получения позиномов вводятся дополнительные ограничения:

• 5. S² + x²₃£ τ²
• 6. x²₁ + x²₂£ μ

Определение степени трудности двух задач осуществляется по формуле:

d=n - m - 1,

где n - общее количество позиномов;

      m - количество оптимизируемых параметров.

Следовательно, для различных вариантов соединения стержней параметр d имеет следующие значения.

• 1.) жёсткое соединение узла С: d=9 - 6 - 1=2;
• 2.) шарнирное соединение узла С: d=8 - 6 - 1=1.

Далее строится матрица экспонент.

• 1.) жёсткое соединение узла С:

;

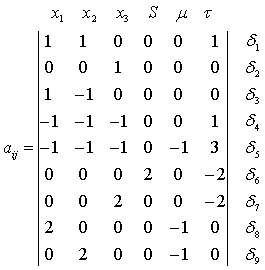• 2.) шарнирное соединение узла С

.

С помощью представленных матриц, из условий нормализации и ортогональности составляется система уравнений имеет следующий вид:

• 1.) жёсткое соединение узла С

;

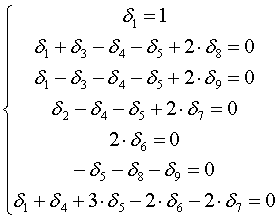• 2.) шарнирное соединение узла С

.

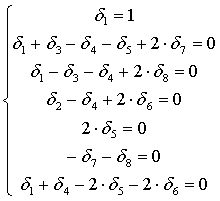Так как количество уравнений в обоих случаях меньше количества неизвестных, то необходимо замкнуть систему введением уравнений равновесия, количество которых равно числу степени трудности d:

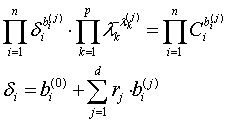
где        b_i⁽⁰⁾ - вектор нормализации; b_i^(j) - вектор невязки; r_i - базисная переменная (их количество равно числу d).

Составляется двойственная функция:

• 1.) жёсткое соединение узла С

;

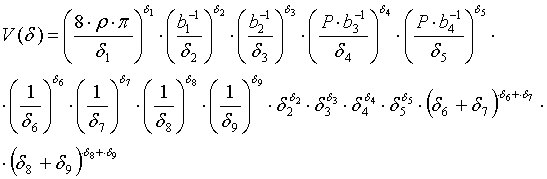• 2.) шарнирное соединение узла С:

.

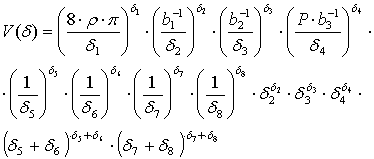Итак, введение дополнительных переменных и ограничений позволило привести задачу в обоих случаях нагружения к такому виду, который позволяет применить обычный алгоритм метода геометрического программирования.