Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

Автоматизированное проектирование технических систем: Учебное пособие.
Бельков В. Н., Ланшаков В. Л.,
3.3.1. Примеры решения вопросов по компоновке оборудования
Следующие примеры показывают возможность применения даже простых методов оптимизации для решения задач компоновки оборудования на ракете. В случае многофакторной оптимизации необходимо использовать метод целочисленного линейного программирования.
Пример 1. В шар данного радиуса R вписать прямой круговой конус максимального объема.
Решение.
Обозначим: R-радиус шара; r-радиус основания конуса; ![]() - высота конуса; где x-расстояние от центра шара до основания конуса.
- высота конуса; где x-расстояние от центра шара до основания конуса.
Используя очевидные соотношения, получим:
![]() ;
; ![]() ;
; ![]() -объем конуса.
-объем конуса.
Следовательно, ![]() .
.
Экстремальные значения определяются из следующего выражения:
![]() .
.
Решая квадратное уравнение, получим:
![]() , т.е.
, т.е.
![]() ;
; ![]()
![]() .
.
Пример 2. Среди всех круговых конусов с данной образующей l, найти корпус с наибольшим объемом.
Решение.
ЦФ имеет вид: ![]() , где R - радиус основания конуса; h - высота конуса.
, где R - радиус основания конуса; h - высота конуса.
Учитывая соотношение: ![]() , можно записать:
, можно записать:
![]() .
.
На основании : ![]()
![]()
![]()
![]() .
.
Следовательно, конус с ![]() и
и ![]() будет иметь наибольший объем.
будет иметь наибольший объем.
Пример 3. Определить размеры а, в и с параллелепипеда заданного объема V, который имел бы минимальную поверхность S.
Решение.
Критерий оптимальности этой задачи (ЦФ) имеет вид:
![]()
Ограничение на параметры a, b и c согласно условию задачи описывается выражением:
![]()
Функция Лагранжа имеет вид:
![]()
Следовательно:
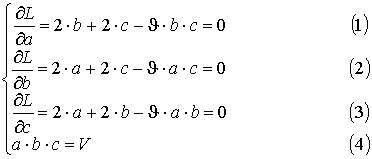 .
.
Для получения расчетных формул выполним следующие действия.
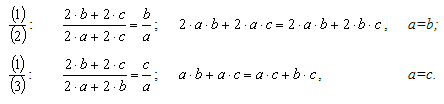 : ; , a=b;
: ; , a=b;
Следовательно: a3=V; a=b=c= ![]() , поэтому
, поэтому ![]() .
.
Пример 4. Разместить в приборном отсеке ракеты приборы двух типов, каждый из которых весит 2 кГ, но один из них трехфункциональный, а другой - двухфункциональный; при этом, учитывая ограничение по общему весу в 7 кГ, добиться максимальной эффективности приборов.
Решение.
Математическая формулировка задачи выглядит следующим образом.
Максимизировать ЦФ ![]() ,
,
при ограничениях: ![]()
где ![]() - целочисленные.
- целочисленные.
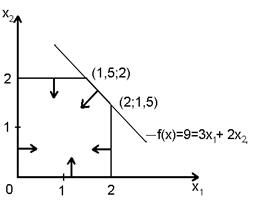
Начальный шаг решения этой задачи состоит в нахождении решения задачи линейного программирования (ЛП), получаемой при отбрасывании условий целочисленности и . Обозначим эту задачу через ЛП-1, решение которой представлено на рис. 3.7.
|
Рис. 3.7. Решение ЛП - 1. |
Найденное значение f (x) представляет собой верхнюю границу истинного оптимального целочисленного значения, поскольку при выполнении условия целочисленности x2 значение f(x) может только уменьшится. |
Следующий шаг метода заключается в просмотре целочисленных значений x2, больших или меньших 1,5. Это делается путём добавления к задаче ЛП-1 либо ограничения ![]() , либо
, либо ![]() . Таким образом, из задачи ЛП-1 получаются две задачи следующего вида ЛП-2 и ЛП-3, представленные соответственно на рис. 3.8 и 3.9.
. Таким образом, из задачи ЛП-1 получаются две задачи следующего вида ЛП-2 и ЛП-3, представленные соответственно на рис. 3.8 и 3.9.
В этих задачах наряду с первоначальным условием соответственно добавлены:
- для ЛП - 2 новое ограничение
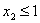 ,
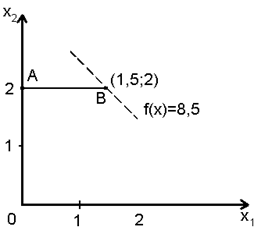
, - для ЛП - 2 новое ограничение x2≥ 2, поэтому допустимая область в этом случае представляет собой просто отрезок АВ.
|
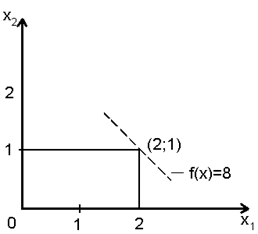
Рис. 3.8. Решение ЛП - 2. |
Рис. 3.9. Решение ЛП - 3. |
Изображённые допустимые области задач ЛП-2 и ЛП-3 обладают следующими свойствами.
- 1. Оптимальное решение задачи ЛП-1 (x1 = 2; x2 = 1,5) недопустимо для обеих задач ЛП-2 иЛП-3. Таким образом, это решение не повторится.
- 2. Любое целочисленное (допустимое) решение исходной задачи допустимо для задачи ЛП-2 или ЛП-3. Таким образом, при введении этих задач не происходит потери допустимых (целочисленных) решений исходной задачи.
Оптимальное решение задачи ЛП-2 - точка x1 = 2; x2 = 1, f(x) =8. Следовательно, значение f(x) =8 представляет собой нижнюю границу максимального значения f(x) для смешанной задачи ЦЛП. Поскольку ранее была получена лишь верхняя граница, равная 9, нельзя утверждать, что решение ЛП-2 оптимально для исходной задачи. Следовательно, необходимо рассмотреть задачу ЛП-3. Однако её решение недопустимо для исходной задачи ЦЛП, поскольку x1 = 1,5, но при этом f(x) =8,5. Поэтому необходимо проверить существование в допустимой области ЛП-3 целочисленного решения, дающего значение f(x) ≥ 8. Для этого рассматриваются задачи ЛП-4 и ЛП-5, получающиеся при добавлении к ЛП-3 ограничений x1 ≤ 1 и x1 ≥ 2 соответственно.
|
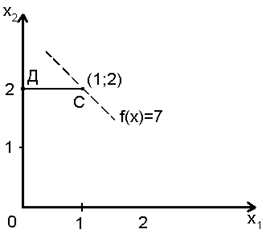
Рис. 3.10. Решение ЛП - 4. |
Допустимая область задачи ЛП-4 состоит из отрезка ДС, показанного на рис. 3.10, задача ЛП-5 не имеет допустимых решений. Итак, точка x1 = 2; x2 = 1, из задачи ЛП-2 представляет собой оптимальное целочисленное решение исходной задачи, так как f(x) =8, т.е. больше f(x) из ЛП-4. |
Удобно представить последовательность задач ЛП, возникающих при использовании процедуры метода ветвей и границ, в виде сети или дерева. Они состоят из множества вершин и соединяющих их дуг или ветвей. Каждая вершина представляет собой либо начальную, либо конечную точку некоторой ветви.
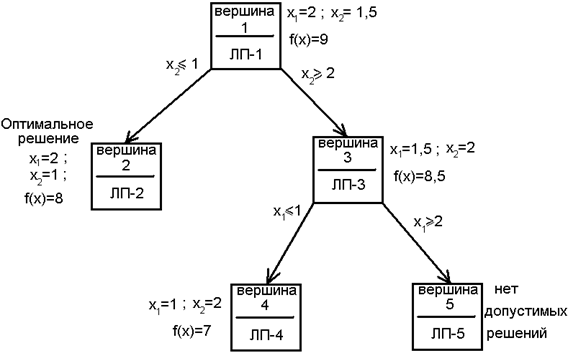
Рис. 3.11. Схема решения.
Вершина 1 соответствует задаче ЛП-1, получаемой из исходной задачи при отбрасывании требования целочисленности переменных. Ветвление в вершине 1, определённое целочисленной переменной с помощью ограничения , приводит к вершине 2 (ЛП-2). Поскольку задача ЛП-2 имеет оптимальное целочисленное решение, нет необходимости производить ветвление в вершине 2. В этом случае, когда в некоторой вершине возникает подобная ситуация, говорят, что рассматриваемая вершина прозондирована. Ветвление в вершине 1 по ограничению даёт ЛП-3 (вершина 3). Поскольку оптимальное решение ЛП-3 является дробным, происходит дальнейшее ветвление в вершине 3 по целочисленной переменной . Таким образом, появляются вершины 4 и 5. Эти вершины являются прозондированными, поскольку ЛП-4 обладает целочисленным решением, а ЛП-5 не имеет допустимых решений. Наилучшее решение из прозондированных в вершинах является оптимальным.