Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Автоматизированное проектирование технических систем: Учебное пособие.

Бельков В. Н., Ланшаков В. Л.,

3.3.2. Цилиндрическая оболочка

Рассмотренную выше задачу 3.1.3 представим в несколько иной постановке, а именно: выполним анализ силового нагружения корпуса ракеты, т.е. цилиндрической оболочки. При этом для иллюстрации возможностей различных методов задачу будем решать методом геометрического программирования.

Математическая модель состоит, как обычно, из ЦФ, которой является вес оболочки (первое уравнение системы), и ограничений на прочность (остальные уравнения следующей системы).

.

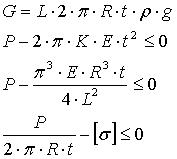В соответствии с требованием алгоритма метода приведем задачу к стандартному виду:

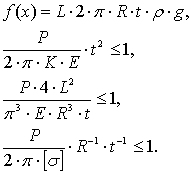   или      ,

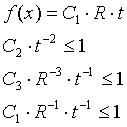где ;             ;

;          .

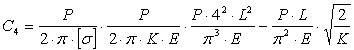Степень трудности данной задачи .

Следовательно, задача сводится к анализу системы нескольких линейных и одного нелинейного уравнения.

При этом матрица экспонент имеет вид:

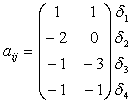
Система линейных уравнений, включающая условия нормализации и ортогональности, преобразуется к виду:

.

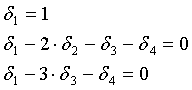Двойственная функция находится из выражения:

.

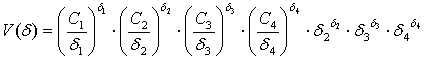На основе разработанной ММ можно записать:

вектор нормализации 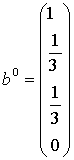,                 вектор невязки .

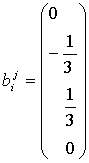Далее запишем уравнение равновесия:

,

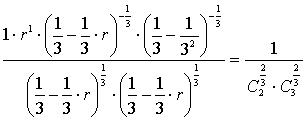из которого можно определить базисную переменную r:

;      ;      ;

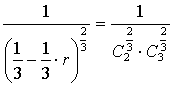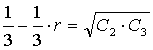В связи с этим, можно записать: ,

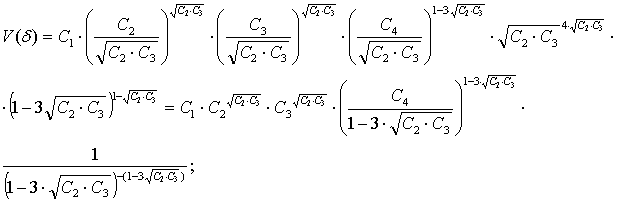
Представленные формулы для двойственной функции и переменных позволяют рассчитать оптимизируемые параметры и вес цилиндрической оболочки по заданным исходным данным.