Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Моделирование конкуренции в условиях рынка

Степанов Л. В.,

1.3 ПОДХОДЫ К МОДЕЛИРОВАНИЮ ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ И СИСТЕМ. ФОРМАЛИЗАЦИЯ РЫНКА В УСЛОВИЯХ КОНКУРЕНЦИИ

В области экономических исследований дальнейший прогресс будет связан с широким ис­пользованием математических методов и моделей. Однако в настоящий момент доминирует качественный анализ. Это связано с тем, что пока плохо выявлены все количе­ственные закономерности, а построенные математические модели охватывают только отдельные участки экономических явлений и процессов.

Поэтому особой актуальностью обладает комплексный подход к рассмотрению той или иной задачи, охватывающий всю экономическую проблему в выбранной области.

Рыночная экономика построена на постоянном поиске наиболее выгодного варианта распределения финансовых, трудовых, товарных, технических и других ресурсов между всеми участниками экономических отношений. В настоящее время усложнение взаимосвязей вне и внутри предприятий, наличие большого числа показателей, фак­торов и ограничений, а также быстрый рост конкуренции не поз­воляют сформировать оптимальный план действий в тех или иных условиях без применения специ­альных методов.

Как отмечалось выше, рыночный процесс представляет собой совокупность опера­ций, направленных на совершение купли-продажи товаров и ус­луг с целью удовлетворения покупательского спроса и получения прибыли. Отдельно стоит отметить, помимо торговли, еще целый комплекс заготовительной, производственной, строитель­ной, инвестиционной и другой дополнительной деятельно­сти, содействующей в конечном итоге решению главной задачи - получению прибыли. При этом также выделяют задачи предвидения коммерческих рис­ков и просчет возможных исходов, последствий принимаемых решений. Несмотря на то, что при принятии коммерческих решений широко ис­пользуются принципы маркетинга, успеха можно достичь, только применяя методы математического моделирования.

Важнейшим элементом рыночной деятельности предприятий является изучение спроса на товары, рынков сбыта, выявление и изучение источников поступлений и поставщиков товаров, организацию рациональных хозяйственных связей с поставщиками, разработ­ку заявок по всему ассортименту товаров, заключение договоров на поставку товаров, организацию и ведение учета и контроля за выполнением договорных обязательств.

Специалисты в сфере экономики должны быть готовы к ре­шению следующих профессиональных задач [106, 110] в условиях рыночных процессов:

1. коммерческо-организационные задачи:

• выбор товаров и формирование ассортимента, подбор покупателей и поставщиков;
• планирование и организация процессов закупки и продаж товаров;
• организация коммерческих взаиморасчетов;
• организация товародвижения и создание системы стимулирования сбыта;
• управление товарными запасами;

2. научно-исследовательские задачи:

• исследование и анализ товарных рынков;
• исследование ассортимента и конкурентоспособности товара;
• исследование и моделирование бизнес-технологий;
• анализ и оценка эффективности коммерческой дея­тельности;
• исследование информационно-методического обеспе­чения коммерческой деятельности с целью ее оптимизации;

3. проектно-аналитическая деятельность:

• проектирование информационного обеспечения коммерческой деятельности;
• прогнозирование конъюнктуры товарных рынков;
• прогнозиро­вание и проектирование номенклатуры товаров;
• прогнозирова­ние и разработка стратегии коммерческой деятельности пред­приятия на товарном рынке;
• прогнозирование результатов коммерческой деятельности предприятия коммерче­ской службой.

Большинство задач имеют прямое или косвенное отношение к конкурентному взаимодействию. Успех решения этих задач зависит от качества и эффективности применяемых математических моделей и методов.

Математи­ческое моделирование экономических процессов и последова­тельное установление логических связей для обеспечения возможности наблюдения, контроля и управления ими, является наиболее эффективным средством для реше­ния различных проблем. Существующие математические методы и модели могут позволить решать задачи большей размерности и учитывать широкий перечень показателей и факторов влияния, а время решения за­дач значительно сокращается с применением компьютеров. Кроме того, в ряде сложных задач не всегда может быть получено оптимальное решение. Речь может идти только о приближении к этому решению.

В качестве средств, применяемых наиболее часто для построения математических моделей некоторых отдельных процессов в экономике, можно рассматривать методы линейного, динамического и целочисленного программирования, теории массового обслуживания, теории графов, сетевого планирования. Они используются для моделирования задач перевозки грузов, оптимизации плана продажи и покупки товаров, назначения и распределения ре­сурсов, анализа устойчивости коммерческой деятельности предприятия и других.

Методы линейного программи­рования позволяют описать некоторый набор хорошо исследованных экономических задач, таких как: планирование товарооборота; размещение розничной торговой сети города; планирование капиталовложений; оптимизация межотраслевых связей торгов­ли. В задачах ли­нейного программирования критерий эффективности и функции в системе ограничений линейны. Если содержательный смысл требует получения решения в целых числах, то такая задача является задачей целочисленного программирования. В задачах параметрического программирова­ния целевая функция или функции, определяющие область воз­можных изменений переменных, зависят от некоторых парамет­ров. Если эти функции носят случайный характер, то имеем зада­чу стохастического программирования. Если в задаче математи­ческого программирования имеется переменная времени, а кри­терий эффективности выражается через уравнения, описывающие протекание операций во времени, то такая задача является задачей динамического программирования.

Теория массового обслуживания рассматривает разнообразные процессы в экономике, как процессы удовлетворения каких-либо запросов и заказов. При всем разнообразии эти процессы имеют общие черты: требования на обслуживание нерегулярно (случайно) поступают в канал обслуживания и в зависимости от его занятости, продолжительности обслуживания и других факторов, образуют очередь требований. Данная теория изучает статистические закономерности поступления требований и на этой основе вырабатывает решения, то есть такие характеристики, при которых затраты времени на ожидание в очереди, с одной стороны, и на простой каналов обслуживания - с другой, были бы наименьшими. Всю систему производства и потребления товаров можно трактовать как систему массового обслуживания, где встречаются люди (клиенты) и товары.

Теория графов - математическая теория, содержание которой формулируется двояко в зависимости от трактовки ее исходного понятия граф: теоретико-множественной или геометрической. В первом случае предметом теории являются графы как некие объекты, определяемые двумя множествами - множеством элементов и множеством бинарных отношений между ними. Во втором случае - свойства геометрических схем (графов), образованных множеством точек и соединяющих их линий. В обоих случаях главное понятие теории - граф, изучаемый как абстракция, независимо от его содержания. Обнаруженные соотношения, закономерности находят применение в самых различных областях экономики. С их помощью можно решать задачи по построению наилучшего плана перевозок продукции от поставщика к потребителям, вырабатывать маршруты различных перевозок, рассчитывать наилучшее распределение рабочих по машинам на производстве и так далее.

Сетевое планирование и управление применяется в экономике для управления процессами, включающими в себя большой набор операций, и основано на использовании ЭВМ и сетевых графиков. С помощью сетевого графика компьютер может произвести анализ состояния процесса в каждый заданный момент времени, определить последовательности работ, которые могут задержать выполнение плана к намеченному сроку (критический путь), и, таким образом, "посоветовать" руководству оперативно принять необходимые меры. Система сетевого планирования ориентирована на какой-либо один критерий: время, стоимость работ и так далее. Реальные сетевые графики содержат сотни и даже тысячи работ и событий. Их анализ возможен только с помощью ЭВМ. В этих условиях сам график теряет преимущество наглядности и тогда применяется цифровое представление сети. Важно, что методы расчетов по сетевым графикам в своей основе стандартны, что позволяет вести расчеты только для однотипных экономических объектов или процессов. Поэтому, сетевое планирование и управление применяется в сочетании с другими экономико-математическими методами, например, теорией массового обслуживания.

Наиболее часто для решения экономических задач применяют аналитические технологии, основанные на методах оптимального управления, решения дифференциальных уравнений и так далее. Для того, чтобы они были применимы, необходимо, чтобы данная задача полностью описывалась определенной детерминированной моделью. В таком случае модель дает точный ответ и показывает свою эффективность.

На практике часто встречаются задачи, связанные с наблюдением случайных величин - например, задача прогнозирования курса акций. Для подобных задач не удается построить детерминированные модели, поэтому применяется вероятностный подход. Такого рода методы предполагают, что известна некоторая вероятностная модель задачи. Например, в задаче прогнозирования курса можно предположить, что завтрашний курс акций зависит только от курса за последние два дня. Если это верно, то наблюдения курса в течение нескольких месяцев позволяют достаточно точно оценить коэффициенты этой зависимости и прогнозировать курс в будущем.

Классические методики оказываются малоэффективными во многих практических задачах. Это связано с тем, что невозможно достаточно полно описать реальность с помощью небольшого числа параметров модели, либо расчет модели требует слишком много времени и вычислительных ресурсов.

В частности, рассмотрим проблемы, возникающие при решении задачи оптимального распределения инвестиций.

• 1. В реальной задаче ни одна из функций не известна точно - известны лишь приблизительные или ожидаемые значения прибыли. Для того, чтобы избавиться от неопределенности, нужно зафиксировать функции, теряя при этом в точности описания задачи.
• 2. Детерминированный алгоритм для поиска оптимального решения (симплекс-метод) применим только в том случае, если все данные функции линейны. В реальных задачах бизнеса это условие не выполняется. Хотя данные функции можно аппроксимировать линейными, решение в этом случае будет далеким от оптимального.
• 3. Если одна из функций нелинейна, то симплекс-метод неприменим, и остается два традиционных пути решения этой задачи. Первый путь - использовать метод градиентного спуска для поиска максимума прибыли. Если в данном случае область определения функции прибыли имеет сложную форму, а сама функция - несколько локальных максимумов, то градиентный метод может привести к неоптимальному решению. Второй путь - провести полный перебор вариантов инвестирования. Если каждая из 10 функций задана в 100 точках, то придется проверить около 10²⁰ вариантов, что потребует несколько месяцев работы даже очень современного компьютера.

Вероятностные технологии обладают существенными недостатками при решении практических задач. Зависимости, встречающиеся на практике, часто нелинейны. Даже если и существует простая зависимость, то ее вид заранее неизвестен. Отметим также, что статистические методы хорошо развиты только для одномерных случайных величин. Если же необходимо учитывать для прогнозирования курса акций несколько взаимосвязанных факторов (например, объем сделок, курс доллара и так далее), то придется обратиться к построению многомерной статистической модели. Такие модели либо предполагают гауссовское распределение наблюдений (что не выполняется на практике), либо не обоснованы теоретически и опираются на малообоснованные эвристические методы.

Другая сторона проблемы - это исходные данные. Использование математических методов связано со сбором необходимой информации, а только затем с постановкой задачи. При сборе нельзя забывать о таких понятиях, как ценность информации и полезность, то есть важность ее для того, кто ее использует. В [17, 75] приведены потери ценности оперативно-тактической и стратегической информации в процентном соотношении. Методы анализа открытой информации приведены в работах [20, 45]. Однако общим для всех методов является сопоставление событий, фактов, намеков, мнений, версий, оценок, слухов, ссылок, то есть самой разнородной информации по некоторым ключевым признакам в зависимости от поставленной задачи, получаемых из различных независимых источников. В условиях экономических систем не все источники информации могут быть одинаково доступны, а данные, полученные из них, полностью достоверны.

Из-за описанных выше недостатков традиционных методик построения математических моделей и особенностей исходной информации следует уделять внимание использованию аналитических систем нового типа. К их числу можно отнести методы теории игр.

Теория игр [39, 48, 120, 121] изучает математические модели принятия решений в ситуациях, при которых интересы участников либо противоположны, и тогда эти модели называются антагонистическими играми, либо не совпадают, хотя и не противоположны, и тогда речь идет об "играх с непротивоположными интересами". Основоположники теории Дж. фон Нейман и О. Моргенштерн попытались математически описать характерные для рыночной экономики явления как некую "игру". В наиболее простом случае речь идет о противоборстве только двух противников, борющихся за какой-либо ресурс. В более сложных случаях в игре участвуют многие, причем они могут вступать между собой в постоянные или временные союзы. Одной из задач теории является выяснение того, возможно ли (и если возможно, то при каких условиях) некоторое равновесие (компромисс), в наибольшей степени устраивающее всех участников. Принципиальным достоинством теории игр считают то, что она расширяет общепринятое понятие оптимальности, включая в него такие важные элементы, как, например, компромиссное решение, устраивающее разные стороны в подобном споре. На практике же игровые подходы применимы при разработке моделей, в которых учитываются интересы различных звеньев экономики. Например: выбор оптимальных решений в области повышения качества продукции и определения запасов. "Противоборство" здесь происходит в первом случае между стремлением выпустить больше продукции (затратить на нее, в расчете на единицу, меньше труда) и сделать ее лучше, то есть затратить больше труда; во втором случае - между желанием запасти ресурсов побольше, чтобы быть застрахованным от случайностей, и запасти поменьше, чтобы не замораживать средства.

В основе другого перспективного направления в технологиях моделирования лежат методы искусственного интеллекта, имитирующие такие природные процессы, как деятельность иммунной системы [52], нейронов головного мозга [79, 102, 124, 125] и процесса естественного отбора [90, 66, 93].

Искусственная иммунная система имитирует поведение защитных функций организма при попадании в него чужеродного тела. Задача иммунной системы в уничтожении этого объекта. Другими словами, иммунитет позволяет поддерживать биологическую систему в состоянии равновесия. В экономике можно встретить немало примеров, когда необходимо аналогичное поведение.

Нейронные сети в каком-то смысле являются имитацией мозга, поэтому с их помощью успешно решаются разнообразные «нечеткие» задачи - распознавание образов, речи, рукописного текста, выявление закономерностей, классификация, прогнозирование и так далее. В таких задачах, где традиционные технологии бессильны, нейронные сети часто выступают как единственная эффективная методика решения. По данным фирмы Ward Systems Group, только в 1998 году программные продукты на основе нейронных сетей использовались более чем в 500 крупнейших компаниях мира из списка Fortune1000 для решения различных задач связанных с экономикой.

Генетические алгоритмы - это специальная технология для поиска оптимальных решений, которая успешно применяется в различных областях науки и бизнеса. В этих алгоритмах используется идея естественного отбора среди живых организмов в природе, поэтому они называются генетическими. Генетические алгоритмы часто применяются совместно с нейронными сетями, позволяя создавать предельно гибкие, быстрые и эффективные инструменты анализа данных.

При выборе тех или иных способов построения моделей необходимо руководствоваться, в первую очередь, условиями и особенностями той задачи, которую планируется решить, характером исходных данных, а также требованиями к точности конечного результата. Совершенно очевидно, что выбор сложных, пусть и прогрессивных, методов для решения несложной задачи негативно скажется на эффективности этого решения и сделает такой выбор необоснованным.

Следует отметить, что иммунные системы, нейросетевые технологии и генетические алгоритмы являются новыми, но интенсивно развивающимися направлениями в области создания моделей объектов, процессов и явлений.

Комплексное использование новых подходов совместно с традиционными методами математического моделирования позволит формализовать и решать задачи высочайшей сложности. Одной из таких задач является конкуренция предприятий в условиях рыночной экономики.

В соответствии с ранее сформулированными определениями и указанными особенностями всех вариантов конкурентного взаимодействия выполним описание и формализацию рыночной системы.

На основе анализа определений 1-3 и характеристик отдельных видов конкуренции можно выделить внутренние факторы, влияющие на участников рыночного процесса. К их числу можно отнести любую экономическую и прочую деятельность, осуществляемую внутри предприятий. Например, управление товарно-сырьевыми запасами, трудовыми и финансовыми ресурсами, производственными мощностями и так далее. Эти факторы напрямую не влияют на конкурентное взаимодействие с другими участниками рынка. Можно утверждать, что конкурентоспособность, согласно определению 8, тогда будет давать субъекту конкурентное преимущество, когда свойства и особенности производимого товара будет опережать характеристики родственных товаров других участников рынка. С позиции конкуренции совершенно неважно, какие внутренние резервы для этого будут необходимы. Именно характеристики товара предлагается рассматривать, как внешние факторы, определяющие состояние конкурентного взаимодействия на рынке.

Применяя системный подход, предлагаем описать рынок следующей структурной схемой (рис.1.4).

В соответствии с определениями 7-8, предлагается выделить два уровня конкуренции:

• 1. Уровень реальной конкуренции - уровень сравнения ценности и полезности товара на основе анализа его ценовых и неценовых особенностей;
• 2. Уровень виртуальной конкуренции - уровень получения конкурентных преимуществ участником рынка при производстве конкурентоспособного товара.

Таким образом, реальное конкурентное взаимодействие осуществляется на первом уровне. Такое представление подтверждает тот факт, что с позиции рыночного процесса не имеет значения, какой деятельностью обеспечены ценовые и неценовые характеристики товара.

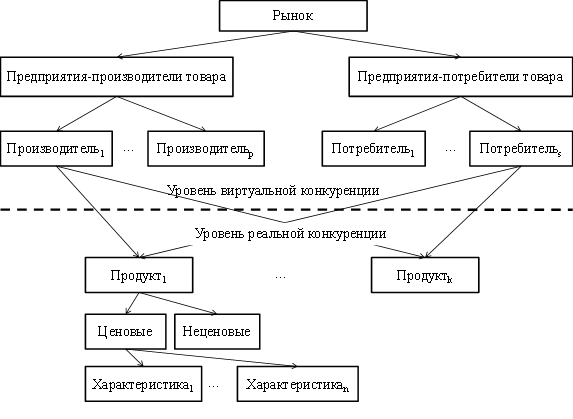
Рис.1.4 Двухуровневая модель структуры рынка

С учетом того, что отдельные виды конкуренции существенно различаются между собой, процесс формализации рынка необходимо осуществить в максимально общей форме, удовлетворяющей всем этим типам и видам.

Согласно определению 1, под математической моделью рынка предлагается понимать совокупность элементов:

R = (PT, PR, G)    (1.3)

где PT - множество потребителей товара; PR - множество производителей товара; G -государство, как регулирующий механизм рынка.

Государство G регулирует отношения на рынке через законодательную базу, создавая такие условия, при которых ни один участник рыночного процесса не станет (не захочет) прибегать к действиям, нарушающим положения этой базы, то есть конкуренция не станет недобросовестной.

При получении государством дополнительной роли кроме регулирующей, получим: G   PT  или G PR.

Тогда в условиях регулируемого рынка, в ситуации участия государства в рыночных отношениях, как производителя или потребителя выражение (1.3) получит вид:

  R = (PT,PR)  при G    PT  v  G    PR.         (1.4)

Рассмотрим более подробно особенности и формирование множеств PT и PR.

Множество потребителей товаров можно описать:

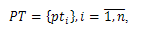,              (1.5)

где n - количество потребителей.

Множество производителей товаров можно описать:

,             (1.6)

где m - количество производителей.

Тогда, исходя из (1.5), (1.6), размер рынка можно было бы определить:

     .                       (1.7)

Выражение (1.7) верно в том случае, если множества PT и PR не содержат ни одного предприятия, сочетающего в рамках данного рынка функции производителя и потребителя.

Теорема 1. Множества PT и PR не пересекаются.

Доказательство:

С позиции теоретико-множественного подхода сочетание в рамках данного рынка функции производителя и потребителя соответствует пересечению множеств [26, 62]:

 PT ∩ PR = { P|P  PT Λ P    PR } .               (1.8)

где P - некоторый участник рынка.

Однако, с позиции экономического смысла конкуренции, выраженного в определении 3, это не верно, так как предприятие P не может соперничать само с собой.

Теорема доказана.

Также неприменимы в полной мере и другие операции над множествами [67, 80].

Для недопущения ситуации с объединением, пересечением множеств и так далее предлагаем следующее. Если один и тот же субъект P выступает и в качестве производителя и в качестве потребителя каких-либо товаров одного рынка он должен быть условно разделен на два - условного потребителя и условного производителя.

Введем операцию условного замещения:

       P : { P^PT , P^PR },                       (1.9)

где P - реальный субъект рынка; P^PT - условный объект рынка с функцией потребителя; P^PR - условный субъект рынка с функцией производителя.

Правомерность этой операции подтверждается экономически:

• 1. в бухучете товары, производимые и приобретаемые, учитываются на различных счетах;
• 2. организационно разделяют отделы сбыта и снабжения, создавая отдельные подразделения;
• 3. при расчете финансовых показателей компоненты доходной и расходной части разделяют;
• 4. и так далее.

Таким образом, можно утверждать, что к PT и PR операции над множествами           [67, 80, 99] не применимы.

Тогда более корректно размер рынка определять:

     |R| = |PT| + |PR|  ,              (1.10)

где |PT| - количество потребителей (включая условных);  |PR| - количество производителей (включая условных).

Теорема 2. Совершенная конкуренция возможна при идеальных условиях.

Доказательство:

Размер рынка можно определить согласно (1.7).

Отметим, что условия совершенной конкуренции, в соответствии с определением 10, предполагают что  n → ∞ и m → ∞.

Тогда  |R| → ∞ - это в реальных условиях невозможно по причине ограниченности рынка.

Тогда совершенная конкуренция возможна только при идеальных условиях.

Теорема доказана.

Теорема 3. На рынке не может отсутствовать один из участников.

Доказательство:

Отсутствие одного из участников на рынке выражается: PT = Ø V PR = Ø

Выполнение этого условия, противоречит определению конкуренции, предполагающей обязательный элемент соперничества и выражению (1.3).

Теорема доказана.

Теорема 4. На рынке не могут отсутствовать оба участника.

Доказательство:

Отсутствие двух участников на рынке выражается: PT = Ø Λ PR = Ø

Выполнение этого условия, противоречит определению конкуренции, предполагающей обязательный элемент соперничества, выражению (1.3), а последнего приведет к отсутствию самого рынка R = Ø, что невозможно.

Теорема доказана.

Наполнением любого рынка является товар. Обозначим T множество товаров производимых (потребляемых) на рынке. Множество Т можно определить, как:

                   ,                      (1.11)

где m - количество производителей; T_j - подмножество товаров j-го производителя.

Важнейшим свойством этого множества является то, что  T ≠ Ø , так как на рынке должен быть представлен хотя бы один товар.

Подмножество товаров j-го производителя:

                    ,                    (1.12)

где l_j - количество товаров j-го производителя.

Любой товар имеет большое количество характеристик. Используя системный подход, товар на рынке можно рассматривать, как сложный объект - систему. В соответствии с одним из свойств систем - разнообразием, любой товар из подмножества T_j должен иметь хотя бы одну особенность, отличающую его от других товаров из T. Такими экономическими отличиями являются неценовые показатели товара (например, торговая марка и имидж товара), а они, в свою очередь, являются признаками производителей.

Объединив (1.11) и (1.12) получаем, что множество T можно определить:

                                 T = { t _jk} ,                       (1.13)

где t_jk - k-й товар j-го производителя.

На основании (1.11) и (1.12) полный ассортимент товара на рынке R можно определить как:

                                                          (1.14)

Обозначим H множество характеристик товара рынка:

            ,                       (1.15)

где H_jk подмножество характеристик k-го товара j-го производителя.

Определим H_jk как:

                                                       (1.16)

где h^y_jk - y-я характеристика k-го товара j-го производителя; w_jk - количество характеристик k-го товара j-го производителя.

Причем:

                                                   (1.17)

где C - ценовые характеристики; NC - неценовые характеристики товара.

Выражение (1.17) носит важный характер, так как согласно положениям маркетинга [1, 2, 4, 33, 41], различие между ценовыми и неценовыми параметрами велико. Только между некоторыми существует взаимное преобразование.

Равноценность двух товаров  t' и  t"  можно было бы выразить:

                                              (1.18)

Однако, на практике такое не возможно, так как полностью идентичных товаров не существует. Кроме того, многие характеристики товара не могут быть выражены числовыми данными. Особенно когда речь идет о показателях неценового характера.

Поэтому, согласно теореме 5, в реальных условиях равноценность товара можно выразить:

                                               (1.19)

Для получения целостной картины в контексте конкурентного взаимодействия, обобщим сделанные утверждения и предположения:

• 1. рынок (1.3) представлен множествами потребителей (1.5) и производителей (1.6);
• 2. размер рынка можно определить согласно (1.10);
• 3. каждый элемент (1.6) производит (элемент (1.5) потребляет) множество товара (1.12);
• 4. благодаря разнообразию характеристик каждый вид товар предлагаем считать уникальным (1.13);
• 5. полный ассортимент товара на рынке можно определить (1.14);
• 6. каждый товар характеризуется множеством ценовых и неценовых параметров (1.15)-(1.17);
• 7. родственный характер товаров предлагается выражать (1.19).

Обобщенная модель рынка имеет вид:

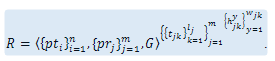.            (1.20)

Таким образом, рынок R предлагается рассматривать, как совокупность непересекающихся множеств потребителей  {pt_i}  и производителей {pr_j} товаров, взаимодействующих с учетом регулирующей функции государства G, с заданным на этой совокупности множестве производимых (потребляемых) товаров {t_jk}  с определенными ценовыми и неценовыми характеристиками {h^y_jk} .

Параметры полученного описания можно использовать для рассмотрения различных видов конкуренции (табл. 1.2). Формализуем определения 10-14:

• 1. Совершенная конкуренция:

                                             n → ∞ Λ m → ∞   ;                                          (1.21)

• 2. Монополия

                         ( n = 1 Λ ∀ m) v (  ∀n Λ m = 1)             ;                            (1.22)  

• 3. Монополистическая конкуренция

   ( n > m Λ T_j ≠ T_j+1 Λ m >1 ) v (m > n Λ T_j ≠ T_j+1 Λ n >1);              (1.23)

• 4. Олигополистическая конкуренция

                   (n >> m Λ T_j ≠ T_j+1 ) v ( m >> n Λ T_j ≠ T_j+1 )    .                     (1.24)            

Таким образом, полученное описание рынка обладает достаточной гибкостью, чтобы отразить все структурные и функциональные особенности конкуренции. Обращает на себя внимание большая размерность рассматриваемой задачи, подтверждающая обоснованность применения новых математических подходов к моделированию конкурентного взаимодействия на рынке.

Важнейшими компонентами предложенной модели (1.20) являются множества потребителей PT и производителей PR товаров (услуг) рынка R, а также само множество производимых (потребляемых) товаров T. Эти три компонента заранее предопределены для любого рынка независимо от вида конкуренции на нем. Следовательно, переменным в модели (1.20) является множество характеристик товаров H. Значения этих характеристик складываются на рынке эволюционно и способ их формирования существенно зависит от структуры рынка, а главное, типа и вида конкуренции на нем. Кроме того, разнообразие параметров, характеризующих различные виды конкуренции, не позволяют построить единую, универсальную математическую модель для всех случаев конкурентного взаимодействия. В связи с этим различные виды конкуренции предлагается рассмотреть отдельно.