Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Моделирование конкуренции в условиях рынка

Степанов Л. В.,

2.2 МОДЕЛИРОВАНИЕ СТРУКТУРЫ РЫНКА НА ОСНОВЕ НЕЙРОСЕТЕВЫХ ТЕХНОЛОГИЙ

Взаимодействие предприятий в условиях совершенной конкуренции можно рассматривать с различных точек зрения. В соответствии с моделью совершенной конкуренции (2.9) их можно выделить три:

• 1. С позиции каждого предприятия-производителя при решении задачи реализации своей производимой продукции (задача 1);
• 2. С позиции каждого отдельного вида товара на рынке (задача 2);
• 3. С позиции общего состояния конкурентного процесса на рынке в целом (задача 3).

В первом случае необходимо рассматривать виртуальный уровень конкуренции (рис.1.20), то есть состояние субъекта и его взаимодействия без учета выпускаемого им товара. Во втором случае рассматривается уровень реальной конкуренции, то есть совокупные характеристики товара без учета того, кем он произведен. Нужно отметить, что третий вариант основан на поиске оптимального («устраивающего» всех производителей и потребителей) состояния рынка в целом. Именно такой вариант является наиболее общим.

Определим эти направления рассмотрения, как задачи, которые должны быть решены в результате моделирования рынка совершенной конкуренции.

В соответствии с (2.9), рынок состоит из большого числа (1.38) независимых элементов (определение 10), самостоятельно определяющих тактику и стратегию своего поведения. В условиях равной осведомленности каждый из участников рыночного процесса стремиться максимизировать свою выгоду, но с учетом аналогичных целей других предприятий.

Предлагается применить для построения модели рынка совершенной конкуренции технологию нейронных сетей.

Основные перспективы использования теории нейронных сетей связаны с решением сложных практических задач. В связи с этим их использование для моделирования конкуренции вполне обосновано. Начало современным моделям нейронных сетей было положено в работе У. Маккаллока и У. Питтса [68]. Была сде­лана попытка эмулировать человеческие способности, классифи­цировать и распознавать образы. Дальнейшее развитие связано с ра­ботой Ф. Розенблатта [88]. Его модель была названа перцептроном. С начала 1980-х годов начался новый виток развития моделей нейронных сетей, связанный с рабо­тами С. Гроссберга, Т. Кохонена, Д. Хопфилда и других, а также влиянием успехов развития оптических технологий и СБИС, способных обеспечить реализацию новых архитектур на практике.

Особый характер сложных проблем не позволяет создавать универсальные сети, вынуждая разрабатывать специа­лизированные нейронные сети для каждой задачи. В настоящее время существует большое количество разнообразных типов сетей. Эти модели отличаются структурой связей, правилами определения весов или правилами обуче­ния и программирования.

Анализ отечественной [103, 64, 58] и зарубежной литературы [115, 126] позволяет сделать вывод, что основное внимание авторов уделяется применению нейросетевых технологий в телекоммуникационных других технических системах. Высокая эффективность нейронных технологий при решении задач адаптивного управления ди­намичными объектами может сделать их незаме­нимыми при создании новых поколений сетей мобильной связи и других беспроводных сетей.

Актуальность исследований искусственных нейронных сетей под­тверждается многообразием их возможных применений.

Современные ЭВМ превосходят чело­века по способности производить числовые и символьные вычисления. Однако если задача выходит за рамки простых вычислительных операций и затрагивает сферы анализа и обобщения информации, компьютерная техника демонстрирует свою несостоятельность по сравнению с человеком. Причина столь значительного различия в их производительности заключена в том, что архитектура биологической нейронной системы со­вершенно не похожа на архитектуру машины фон Неймана [41], а это существенно влияет на типы функций, которые более эффек­тивно исполняются каждой из моделей.

Нейронная сеть - это сеть с конечным числом слоев из однотипных элементов - аналогов нейронов с различными типами связей между слоями [103]. При этом число нейронов в слоях выбирается исходя из не­обходимости обеспечения заданного качества решения задачи, а число слоев нейронов - как можно меньшее для сокращения времени решения задачи.

Хотя один нейрон и способен выполнять простейшие процедуры рас­познавания, сила нейронных вычислений проистекает от соединений ней­ронов в сетях.

Исследований возможности применения нейросетевых технологий в сфере организационного управления и экономических системах крайне мало. Это делает особенно актуальным построение модели совершенной конкуренции в условиях рыночной экономики с использованием базовых положений данной технологии.

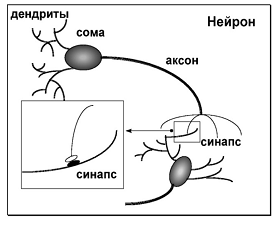
Рис.2.1 Биологический нейрон

На рис. 2.1 показана структура пары типичных биологических нейронов. Дендриты идут от тела нервной клетки к другим нейронам, где они принимают сигналы в точках соединения, называемых синапсами. Принятые синапсом входные сигналы подводятся к телу нейрона - соме. Здесь они суммируются, причем одни входы стремятся возбудить нейрон, другие - воспрепятствовать его возбуждению. Когда суммарное возбуждение в теле нейрона превышает некоторый порог, нейрон возбуждается, посылая по аксону сигнал другим нейронам. У этой функциональной схемы много усложнений и исключений. Однако, для рыночного процесса такого рассмотрения вполне достаточно.

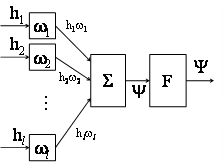
Рис.2.2 Искусственный нейрон

Искусственный нейрон (рис. 2.2) имитирует свойства биологического нейрона. На вход искусственного нейрона поступает некоторое множество сигналов, каждый из которых является выходом другого нейрона. Каждый вход умножается на соответствующий вес, аналогичный синаптической силе, и все произведения суммируются, определяя уровень активации нейрона. Множество входных сигналов (обозначим H) поступает на искусственный нейрон. Эти входные сигналы соответствуют сигналам, приходящим в синапсы биологического нейрона. Каждый сигнал умножается на соответствующий вес ω₁, ω₂,..., ω_l, и поступает на суммирующий блок, обозначенный Σ. Каждый вес соответствует «силе» одной биологической синаптической связи. Множество весов в совокупности обозначается вектором Ω. Суммирующий блок, соответствующий соме, складывает взвешенные входы алгебраически, создавая выход ψ:

                                                                                          (2.10)

Сигнал ψ далее преобразуется активационной функцией F и дает выходной нейронный сигнал Ψ:

                                                      Ψ=F(ψ).                                                   (2.11)

Таким образом, работа искусственного нейрона сводится к преобразованию входного вектора H в некоторое значение функции Ψ на выходе.

Применим данную концепцию к условиям совершенной конкуренции.

Каждый товар из T (2.4) имеет множество ценовых параметров (2.5). Следовательно, этот факт можно отразить одним нейроном (рис.2.4).

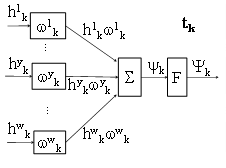
Рис.2.3 Искусственный нейрон k-го товара

Правомочность суммирующего блока Σ подтверждается тем, что все учитываемые параметры товара t_k носят ценовой характер. Неценовые параметры товара в условиях совершенной конкуренции не учитываются.

Однако, на рынке независимо функционируют m производителей из PR, которые выпускают одинаковый ассортимент стандартизованного товара. Таким образом, согласно (2.5) k-й товар у разных производителей имеет одинаковый набор параметров {h¹_k, ..., h^y_k, ..., h^w_k}. Тогда каждый товар будет описываться вектором характеристик, число которых будет равно числу производителей на рынке.

Для получения этих характеристик необходимо построить нейронную сеть. Для этого важно определить наилучшую структуру сети, то есть оптимальное число скрытых слоев и число нейронов в них.

Непрерывная функция может быть аппроксимирована с высокой точностью нейросетью с единственным слоем, но неограниченным числом нейронов. Практически реализовать такую сеть невозможно. При ограничении числа нейронов возрастает ошибка сети. Это может потребовать ее периодического переобучения. Нейросеть с скрытым слоем обладает лучшей способностью к обобщению при ограниченном числе нейронов, но процесс ее обучения становится сложнее. С одной стороны, слишком малое количество скрытых нейронов приводит к недостаточной способности сети к обобщению. С дру­гой же стороны, слишком большое количество скрытых нейронов приводит к увеличению времени обучения и времени реакции (отклика) обученной сети. Предложено значительное количество методов, позволяющих определить чис­ло скрытых нейронов. Часть из них основана на том, что скрытые нейроны добавляются во время процесса обучения, другие методы, наоборот, использу­ют удаление их в ходе этого процесса [94], [108].

С учетом особенностей решаемой задачи предлагается для выбора архитектуры сети руководствоваться требованиями точности функционирования сети, а также сложности и протяженности процесса ее обучения.

В силу того, что все учитываемые параметры товара t_k носят ценовой характер, в качестве активационной функции может быть выбрана линейная зависимость между выходом и входами нейрона. Это обосновывается тем, что характеристика k-го товара у j-го производителя может линейно изменяться при соответствующем изменении входного вектора параметров. Однако в этих условиях может возникать дополнительная неточность при отклонении входных значений от величин обучающей выборки. Если некоторая неточность допустима, то предлагается представить k-й товар всех производителей однослойной нейронной сетью NS_k с линейной активационной функцией (рис.2.4).

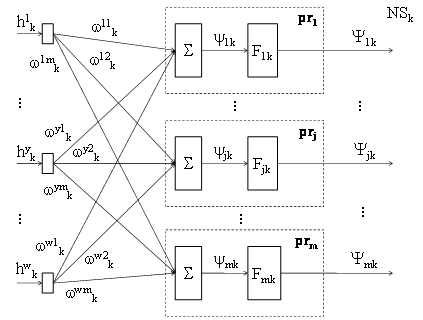
Рис.2.4 Искусственная нейронная сеть NS_k k-го товара с линейной функцией

В нейронной сети (рис.2.4) вектор {Ψ_1k, ..., Ψ_jk, ..., Ψ_mk} представляет собой взвешенные характеристики k-го товара всех производителей. Число нейронов равно числу производителей. Такая сеть обеспечит высокую скорость реакции и обучения, но даст некоторую неточность выходных параметров, особенно когда в качестве входных параметров ей предъявляются значения, не использованные в процессе обучения.

В случае если требуется высокая точность и допустимо большее время на реакцию и обучение сети предлагается двухслойная нейронная сеть с нелинейной активационной функцией (рис.2.5).

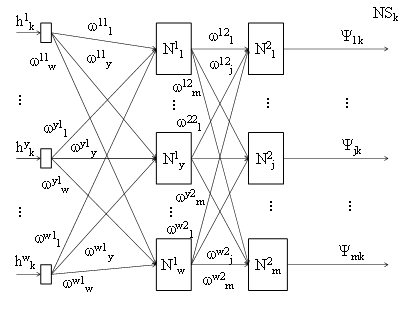
Рис.2.5 Искусственная нейронная сеть NS_k k-го товара с нелинейной функцией

В нейронной сети (рис.2.5) вектор {Ψ_1k, ..., Ψ_jk, ..., Ψ_mk} также представляет собой взвешенные характеристики k-го товара всех производителей. Число нейронов скрытого слоя равно числу характеристик k-го товара, а количество нейронов выходного слоя равно числу производителей. Такая сеть обеспечит достаточно высокую точность выходных параметров для рассматриваемой проблемы.

Однако для решения поставленных выше задач создания одной нейронной сети для всего рынка недостаточно, поэтому предлагается создать нейронную систему.

Определение 16. Под нейронной системой рынка совершенной конкуренции будем понимать совокупность взаимосвязанных реально или условно по выходам и (или) входам нейронных сетей сегментов рынка, объединенных в единую структуру.

Согласно (2.9), в этой системе выделим две подсистемы:

• 1. Производственный сегмент - подсистема производителей товара;
• 2. Потребительский сегмент- подсистема потребителей товара.

На рынке R независимо функционируют m производителей l-го количества товаров. Тогда производственный сегмент рынка можно представить совокупностью из l независимых нейронных сетей (рис.2.6).

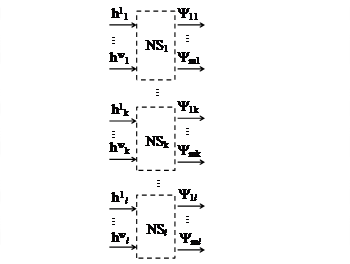
Рис.2.6 Искусственные нейронные сети первого слоя нейронной системы

Таким образом, первый слой нейронных сетей производственного сегмента рынка представляет собой подсистему нейронной системы. Полученное множество векторов {{Ψ}₁, ..., {Ψ}_k, ..., {Ψ}_l} отражает совокупную характеристику всех товаров из T всех производителей из PR. Общий объем множества равен .

Однако, такой вариант рассмотрения рыночного процесса не позволяет охарактеризовать каждый товар или каждого производителя в целом.

Дополним производственную подсистему нейронной системы рынка вторым слоем. Причем этот слой должен иметь два уровня, обеспечивающих независимое решение задачи 1 и задачи 2.

Рассмотрим уровень общения характеристик производителей (задача 1) (рис.2.7). Слой состоит из m нейронов. Каждый нейрон этого слоя представляет собой производителя товара pr_j. Данный слой связывает независимые нейронные сети предыдущего слоя системы в единую структуру. Задача слоя состоит в объединении отдельных характеристических величин по признаку производителя товара.

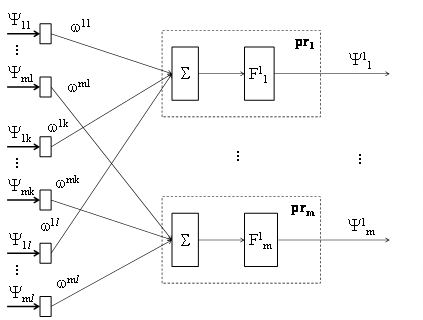
Рис.2.7 Искусственная нейронная сеть первого уровня второго слоя

Таким образом, из l x m  характеристических величин Ψ получаем m выходов Ψ¹. Причем, Ψ¹_j, являющаяся характеристикой j-го производителя на рынке R, фактически представляет собой взвешенную величину, которая учитывает параметры других участников рынка. Особо следует отметить, что значения весовых коэффициентов из Ω позволят учесть влияние товаров из T, если они для данного производителя имеют различную значимость.

По аналогии с рис.2.7 второй уровень второго слоя предлагается представить из                   l нейронов (рис.2.8). Каждый нейрон представляет собой товар t_k.

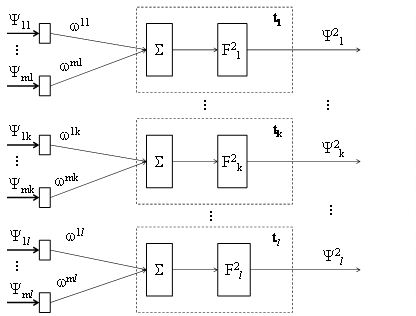
Рис.2.8 Искусственная нейронная сеть второго уровня второго слоя

Таким образом, l выходов Ψ²_k являются характеристиками каждого из товаров рынка R, что соответствует решению задачи 2, поставленной выше. Особо следует отметить, что значения весовых коэффициентов позволят учесть влияние производителей из PR если они для данного товара имеют различную значимость.

Для решения задачи 3 необходимо выполнить обобщение отдельных характеристических величин Y для получения единого параметра, описывающего всю производственную подсистему в целом. Для этой цели необходим третий слой. Он будет состоять из одного нейрона. Причем совокупный показатель можно формировать, как на основе характеристик Y¹, так и на основе Y² (рис.2.9).

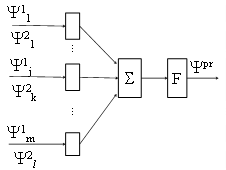
Рис.2.9 Искусственный нейрон k-го товара

Величина Ψ^pr является характеристикой состояния всего производственного сегмента рынка.

В результате получаем сложную архитектуру производственной подсистемы нейронной системы рынка (рис.2.10).

Аналогично можно построить архитектуру нейронной подсистемы потребительского сегмента рынка R.

В результате нейронная система рынка R имеет вид, представленный на рис.2.11.

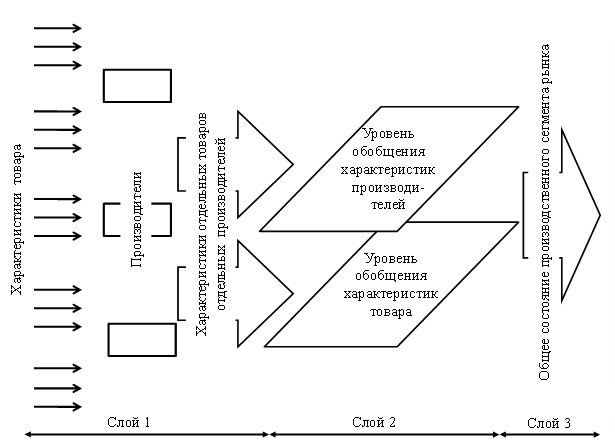
Рис.2.10 Обобщенная архитектура производственного сегмента рынка

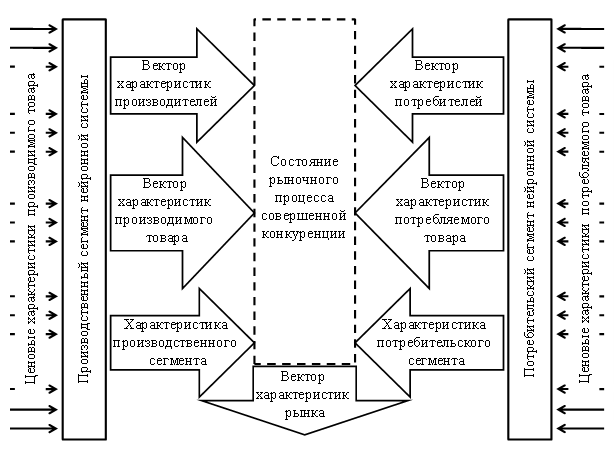
Рис.2.11 Нейронная система рынка

Совокупность векторов характеризует состояние рыночного процесса в условиях совершенной конкуренции. При этом характеристики производственного и потребительского сегмента представляют собой агрегированные величины, полученные на основе векторов характеристик товара. Эти векторы соответствуют виртуальному и реальному уровню конкуренции на рынке, а также тому, какой из этих уровней рассматривается в реальной ситуации.

Общая характеристика производственного сегмента и общая характеристика потребительского сегмента, полученные с помощью третьего слоя, позволяют судить о состоянии рынка в целом. При равенстве их значений состояние рынка можно считать равновесным. Однако, в силу большого (бесконечно большого) числа участников рыночного процесса, такую ситуацию можно считать идеальной.

Для реализации механизмов памяти в процессе длительной эксплуатации следует производить проверку правильности функционирования системы. При отклонении характеристических значений необходимо производить переобучение нейронных сетей.

Предложенная архитектура зависима от изменения числа товаров или субъектов на рынке. Однако, характер связей нейронов не является сложным и может быть легко изменен. Число уровней системы при любом числе субъектов неизменно.

Следующим этапом применения нейросетевых технологий является выбор активационной функции нейронов сети, а также определение весовых коэффициентов входных каналов (синапсов), осуществляемое на основе процесса обучения сети.