
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.4 ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНЫХ ХАРАКТЕРИСТИК ТОВАРА НА ОСНОВЕ ГЕНЕТИЧЕСКОГО АЛГОРИТМА
В результате использования нейронных сетей производственного и потребительского сегмента нейронной системы рынка и подстановки реальных значений ценовых параметров товаров, всех субъектов рыночных отношений могут быть получены две пары множеств:
- 1. Множество характеристик производителей и множество характеристик потребителей для каждого товара;
|
|
pr1 |
... |
prj |
... |
prm |
|
|
pt1 |
... |
pti |
... |
ptn |
|
|
|
t1 |
Ψpr11 |
... |
Ψpr1j |
... |
Ψpr1m |
|
t1 |
Ψpt11 |
... |
Ψpt1i |
... |
Ψpt1n |
|
|
|
... |
... |
... |
... |
... |
... |
|
... |
... |
... |
... |
... |
... |
|
|
|
tk |
Ψprk1 |
... |
Ψprkj |
... |
Ψprkm |
, |
tk |
Ψptk1 |
... |
Ψptki |
... |
Ψptkn |
, |
(2.27) |
|
... |
... |
... |
... |
... |
... |
|
... |
... |
... |
... |
... |
... |
|
|
|
tl |
Ψprl1 |
... |
Ψprlj |
... |
Ψprlm |
|
tl |
Ψptl1 |
... |
Ψptli |
... |
Ψptln |
|
|
где Ψprkj,Ψptki -характеристики j-го производителя и i-го потребителя k-го товара на рынке совершенной конкуренции.
- 2. Множество обобщенных показателей каждого производимого товара и множество обобщенных показателей каждого потребляемого товара.
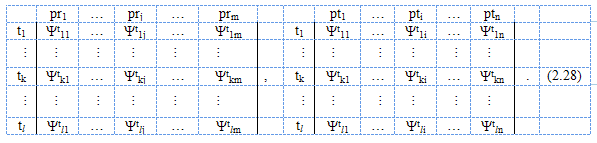
Это соответствует двум уровням рассмотрения конкуренции, как соперничества субъектов рыночных отношений и как соперничества ценовых параметров товара. При условии, что неценовые параметры при совершенной конкуренции не учитываются. Эти множества описывают состояние участников рыночного процесса в условиях конкуренции.
Однако, для описания состояния рынка в целом необходимо получить результирующий вектор путем агрегирования состояний отдельных производителей и потребителей товаров. Процесс получения такого вектора должен учитывать противоположность интересов субъектов рыночных отношений: производители стремятся максимизировать прибыть, а потребители - потребительскую выгоду от получения товара, то есть, в случае совершенной конкуренции, минимизировать издержки, связанные с получением и владением товаром. Требуется решить задачу многокритериальной оптимизации.
Предлагается для получения вектора состояния рыночного процесса применить методы генетического алгоритма.
Генетические алгоритмы относятся к методам случайного поиска решения задач оптимизации. Они основаны на имитации механизмов естественного отбора и природных генетических механизмов (выживание наиболее приспособленных). Если целевые функции в решаемых задачах оптимизации являются многоэкстремальными или пространства поиска частично нерегулярны, требуются алгоритмы, обладающие высокой работоспособностью для предотвращения «застревания» в локальных оптимумах. Достоинством генетических алгоритмов как раз и является способность получать действительно глобальное оптимальное решение.
Генетические алгоритмы (эволюционные программы, эволюционные стратегии и генетическое программирование) достаточно подробно описаны в книгах [90, 66, 93]. Они нашли широкое применение для решения различных задач, таких как задачи оптимального управления, транспортная задача, задача коммивояжера, задачи теории графов, задача составления расписания, задача планировки и размещения объектов, статистические задачи, распознавание образов, задача выбора маршрута, оптимизация сетей. Однако, в рамках моделирования конкурентных процессов примеры их применения отсутствуют.
Один из важнейших элементов, используемых при формировании генетического алгоритма - хромосома. Хромосома представляет собой некоторый код, поставленный в соответствие решению оптимизационной задачи, но не обязательно само это решение.
В соответствии с (2.27) и (2.28) хромосомой будем считать вектор-столбец значений характеристик.
![]()
Благодаря применению нейронных сетей значения хромосом являются однородными. Это связано с симметричным использованием одинаковых активационных функций в производственном и потребительском сегментах. Длины хромосом равные, так как все производители и потребители используют одинаковый ассортимент товара.
Работа генетического алгоритма начинается с формирования набора сгенерированных случайным образом хромосом, называемого популяцией.
Однако, рыночные процессы являются закономерными, в силу регулирующей роли государства, и происходят согласно определенным правилам. В связи с этим случайная генерация недопустима. Популяцией рынка совершенной конкуренции предлагается считать множество характеристических значений, составленное двумя наборами хромосом - производителей и потребителей товаров.

Число элементов-особей в популяции - это некоторое наперед заданное целое число, называемое размером популяции. В условиях данной задачи размер популяции равен , где m - число производителей; n - потребителей товаров на рынке.
Оценка жизнеспособности хромосом в популяции состоит в расчете функции приспособленности для каждой хромосомы этой популяции. Чем больше значение этой функции, тем выше «качество» хромосомы. Форма функции приспособленности зависит от характера решаемой задачи. Предполагается, что функция приспособленности всегда принимает неотрицательные значения.
Исходя из особенностей решаемой задачи, предлагается определять приспособленность, как среднегеометрическую величину характеристических значений хромосомы:
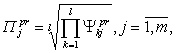 (2.31)
(2.31)
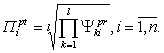 (2.32)
(2.32)
В популяции количество хромосом производителей и потребителей может не совпадать. Такая ситуация возможно только при рассмотрении уровня реальной конкуренции (2.27). Возможны два случая:
m > n , (2.33)
m < n . (2.34)
В обоих случаях необходимо привести состояние популяции к равновесному: . Для этого предлагается применить один из двух способов:
1. Метод рулетки. Каждой хромосоме может быть сопоставлен сектор колеса рулетки, величина которого устанавливается пропорциональной значению функции приспособленности данной хромосомы. Поэтому, чем больше значение функции приспособленности, тем больше сектор на колесе рулетки. Все колесо рулетки соответствует сумме значений функции приспособленности всех хромосом, рассматриваемой популяции. Каждой хромосоме соответствует сектор колеса V, выраженный в процентах согласно формулам:
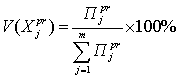 (2.35)
(2.35)
или
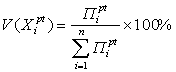 . (2.36)
. (2.36)
Отбор хромосомы может быть представлен, как результат поворота колеса рулетки, поскольку «выигравшая» (т.е. выбранная) хромосома относится к выпавшему сектору этого колеса. Очевидно, что чем больше сектор, тем больше вероятность «победы» соответствующей хромосомы. Поэтому вероятность выбора данной хромосомы оказывается пропорциональной значению ее функции приспособленности. Если всю окружность колеса рулетки представить в виде цифрового интервала [0, 100], то выбор хромосомы можно отождествить с выбором числа из интервала [а, b], где а и b обозначают соответственно начало и окончание фрагмента окружности, соответствующего этому сектору колеса. В этом случае выбор с помощью колеса рулетки сводится к выбору числа из интервала [0, 100], которое соответствует конкретной точке на окружности колеса.
2. Отбор наиболее характерных хромосом. Заключается в исключении хромосом с минимальной (при уменьшении множества хромосом производителей) или максимальной (при уменьшении множества хромосом потребителей) приспособленностью, так как они в меньшей степени соответствуют целям производителей и потребителей, соответственно:
![]() (2.37)
(2.37)
или
![]() . (2.38)
. (2.38)
Операции (2.37) или (2.38) выполняются до тех пор пока: . Правомерность этих операций подтверждается желанием производителей максимизировать свою прибыль, а потребителей минимизировать издержки.
Применение метода рулетки в рамках генетического алгоритма можно рассматривать, как реализацию процедуры случайной мутации, являющуюся одним из элементов естественного отбора, что делает первый способ более предпочтительным. Однако, существует вероятность, что в результате такого отбора из популяции буду исключены хромосомы с высокой приспособленностью. Это негативно скажется на результате работы алгоритма. В генетическом алгоритме мутация хромосом может выполняться на популяции родителей перед скрещиванием либо на популяции потомков, образованных в результате скрещивания.
В случае рассмотрения уровня реальной конкуренции (2.28) количества хромосом изначально равны и равны количеству товара l. В результате рассмотренного процесса создается родительская популяция, также называемая родительским пулом с численностью m + n при условии m = n.
Применение генетических операторов к хромосомам, отобранным с помощью селекции, приводит к формированию новой популяции потомков от созданной на предыдущем шаге родительской популяции. Основным оператором является оператор скрещивания.
На первом этапе скрещивания выбираются пары хромосом из родительской популяции (родительского пула). Предлагаются к рассмотрению следующие варианты формирования пар:
- 1. формирование пар в порядке следования хромосом во множествах производителей и потребителей;
- 2. случайное формирование пар на основе метода рулетки;
- 3. формирование пар на основе максимизации (минимизации) функции приспособленности.
Первые два варианта формирования пар равнозначны и носят случайный характер, что наиболее соответствует природным процессам. Третий вариант формирования является управляемым. Он не отражает суть реальных явлений, но с позиции экономического смысла задачи он вполне применим и может быть выражен:
![]() (2.39)
(2.39)
Далее для каждой пары отобранных таким образом родителей разыгрывается позиция гена (локус) в хромосоме, определяющая так называемую точку скрещивания. Если хромосома каждого из родителей состоит из L генов, то очевидно, что точка скрещивания z представляет собой натуральное число, меньшее L. Поэтому фиксация точки скрещивания сводится к случайному выбору числа из интервала [1, L-1].
В результате скрещивания пары родительских хромосом получается следующая пара потомков:
- 1. потомок, хромосома которого на позициях от 1 до z состоит из генов первого родителя, а на позициях от z+1 до L - из генов второго родителя;
- 2. потомок, хромосома которого на позициях от 1 до z состоит из генов второго родителя, а на позициях от z+1 до L - из генов первого родителя.
Хромосомы, полученные в результате применения генетических операторов к хромосомам временной родительской популяции, включаются в состав новой популяции, для которой вновь рассчитываются значения функции приспособленности для всех хромосом этой популяции. После чего переходят к селекции хромосом полученной популяции.
Новая популяция формируется с помощью процесса отбора, используя некоторый механизм выборки, основанный на значениях функции приспособленности. Процесс селекции предлагается выполнять однократным применением выражений (2.37) и (2.38) к хромосомам производителей и потребителей имеющейся популяции.
В результате популяция сокращается на две «наихудшие» хромосомы. После чего повторяются все шаги, начиная со скрещивания.
Цикл перехода от одной популяции к следующей называется поколением. В каждом новом поколении все хромосомы модифицируются с помощью операций скрещивания. Полученные новые хромосомы называются потомками. Процесс отбора указывает хромосомы, которые войдут в новую популяцию, после чего генетическая система входит в следующий цикл (поколение).
Определение условия остановки генетического алгоритма зависит от его конкретного применения. В оптимизационных задачах, если известно максимальное (или минимальное) значение функции приспособленности, то остановка алгоритма может произойти после достижения ожидаемого оптимального значения, возможно - с заданной точностью. Остановка алгоритма также может произойти в случае, когда его выполнение не приводит к улучшению уже достигнутого значения. Алгоритм может быть остановлен по истечении определенного времени выполнения либо после выполнения заданного количества итераций. Если условие остановки выполнено, то производится переход к завершающему этапу выбора «наилучшей» хромосомы. В противном случае на следующем шаге выполняется селекция.
В данных условиях итогом работы алгоритма будем считать пару хромосом, полученных в результате ряда последовательных селекций (2.37) и (2.38). В силу того, что процесс скрещивания можно рассматривать, как последовательное усреднение характеристик, то в результате будут получены две хромосомы со значениями приспособленности:
![]() . (2.40)
. (2.40)
Если число хромосом производителей и потребителей первоначальной популяции было не равно, то могут быть рассмотрены новые итерации алгоритма, начиная с этапа достижения условия равновесия (мутации): . Целью этих повторений может быть приближение к оптимальному результату:
Пjpr - Пipt ≤ β, при β → 0 , (2.41)
где β - допустимая величина ошибки, определяемая экспертным путем.
Так же, для повышения точности можно выполнить новую генерацию точки скрещивания хромосом.
Аналогично можно применить генетический алгоритм и к множеству (2.28).
После достижения заданной степени точности вектор характеристик рынка можно считать определенным:
Rez = ( Xpr , Xpt ) (2.42)
или в более полной форме:
![]() , (2.43)
, (2.43)
где Ψkpr , Ψkpt - характеристические значения товаров из T.
Для повышения наглядности предлагается обобщить предложенные методологические решения в виде пошагового алгоритма:
- 1. На основе нейронной системы сформировать множества характеристических значений (2.27) или (2.28).
- 2. Рассчитать приспособленность хромосом (2.31) и (2.32).
- 3. Если m ≠ n, выполнить мутацию - уравнивание количества хромосом производителей (2.37) или потребителей (2.38) исходной популяции (2.27) или (2.28).
- 4. Формирование пар хромосом (Xpr, Xpt).
- 5. Выполнение скрещивания.
- 6. Отбор хромосом производителей (2.37) или потребителей (2.38).
- 7. Рассчитать приспособленность хромосом (2.31) и (2.32).
- 8. Если в полученной популяции более 2 хромосом, переход к шагу 4, иначе к шагу 9.
- 9. Если условия (2.40) или (2.41) не выполняются, повторить с шага 3 новую мутацию, иначе шаг 10.
- 10. Получен оптимальный вектор Rez (2.42).
Полученные параметры являются наиболее рациональными, так как не только учитывают положение на рынке других субъектов внутри множеств PR и PT, но и являются оптимальными с учетом соперничества и противоположности интересов всех участников рынка R в целом.
Следовательно, каждый prj и pti, исходя из собственных интересов, может независимо, используя нейрон (рис.2.3), или с учетом других субъектов своего сегмента, используя нейронную сеть (рис.2.4) или (рис.2.5), получить характеристическое значение товара и сравнить его со значением из (2.42). Любые различия будут приводить к отклонению от оптимального поведения на рынке.
Зная характеристическое значение Ψ, используя нейрон (рис.2.3) каждого товара, путем обратного распространения сигнала можно получить точные значения параметров товара {hk}.
Отклонения в большую сторону от (2.43) для каждого из производителей будет приводить к потере конкурентного преимущества по сравнению с другими участниками рыночных отношений, так как увеличение ценовых характеристик товара будет связано с потерей потребителей. Отклонение в меньшую сторону будет уменьшать получение выгод от реализации продукции.
Аналогично отклонение от (2.43) будет сказываться на конкуренции среди потребителей, приводя, в зависимости от обстоятельств, к потере конкурентного преимущества или к недостаточному получению выгод.
