
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
3.2 ТЕОРИЯ ИГР И КОНКУРЕНЦИЯ В УСЛОВИЯХ МОНОПОЛЬНОГО РЫНКА. ФОРМАЛИЗАЦИЯ ИГРЫ
При анализе функционирования рыночных систем исследователю, как правило, требуется для сужения задачи осуществлять процесс выбора тех потребителей, которые наиболее полно отражают цель и свойства всей системы в целом. Решение данной проблемы обычно основывается на применении средств и методов математического моделирования.
При реализации различных процессов, связанных с моделированием, необходимость в выборе возникает, как правило, на этапах структурного и параметрического синтеза системы, когда исследователю в соответствии с определенными целями объектов требуется осуществить выбор качественного и количественного состава элементов данной системы. Вместе с тем хорошо известно [25, 74], что указанные этапы являются важнейшими элементами любого процесса моделирования, так как от качества их выполнения во многом зависит эффективность функционирования рынка. Это заставляет при решении той или иной задачи в рамках моделирования отыскивать не просто приемлемые, а оптимальные решения. Их получение связано с применением эффективных средств автоматизированного поиска вариантов, базирующихся на новейших достижениях компьютерной технологии и современных методах вычислений.
Многоцелевой характер задачи [25, 97] определяется тем, что в рамках реализации исследуемого процесса нельзя ограничиться достижением какой-либо одной цели, а необходимо преследовать сразу несколько, часто конфликтующих, целей. Многоальтернативность решений [97, 96] состоит в том, что возможны ситуации, когда в результате решения приходится выбирать лучший вариант из нескольких альтернативных. Причина появления совокупности таких решений заключается в том, что ни одно из них нельзя считать заведено лучшим сразу по всем критериям оптимизации [23, 32, 33]. Рынок, как и многие системы, считается открытой [25, 96] структурой, если существуют другие, связанные с ней системы, которые оказывают на нее воздействие и на которые она тоже влияет. В данном контексте рынок можно рассматривать как замкнутую систему, вне связи с внешней средой.
Кроме того, необходимо использование проверки согласованности, непротиворечивости и полноты информации.
Основной составной частью процесса управления, в том числе и в экономике, является принятие решений (ПР). В настоящее время имеется большое количество работ по теории принятия решений [29, 30], ее процедурам [22, 101, 111] и методам, основанным на многоцелевой оптимизации, например, с помощью метода нахождения оптимальных по Парето точек выпуклого множества [53]. Наиболее известными являются работы П. Фишберна, Р.Л. Кини и X. Райфа, Р.Д. Льюса, М.А. Айзермана и других ученых.
Однако разработки в этом направлении не содержат подходов, позволяющих реализовать требования и особенности рассматриваемой задачи моделирования конкуренции, такие как, неопределенность описания свойств и характеристик товаров (недостаток количества исходной информации), а так же антагонистический характер взаимодействия монополиста и потребителей.
Одним из главных признаков неопределенности вариантов поведения потребителей является качественный характер описания неценовых свойств товара. При этом перечисленные выше методы оказываются неэффективными в силу того, что используемая для их работы исходная информация должна быть аналитического характера.
Наличие разного рода неопределенности при описании потребителей относится и к тому, что исходная информация может быть противоречива и недостаточно полна. Наряду с качественным описанием присутствуют и количественные оценки. По мере решения поставленной задачи могут возникать данные, требующие учета или корректировки, что является примером методов сравнения.
Как видно из представленного выше обзора, теория принятия решений не содержит одного универсального метода. Большинство приведенных выше методов не допускают их совместного использования или не гарантируют непротиворечивости результатов, а наличие развитой качественной и количественной информации, подлежащей обработке, делают их применение крайне неудобным и малоэффективным.
Весьма перспективным направлением в теории исследования динамики поведения элементов системы являются формализованные теоретико-игровые модели.
Методологические, теоретические и прикладные аспекты теории игр обстоятельно рассмотрены в книгах Дж. Неймана и О. Моргенштерна, Б. Гермейера, Н.Н. Воробьева и других ученых. Общие вопросы построения теоретико-игровых моделей и многие принципы оптимальности подробно обсуждаются в книге Р.Д. Льюса и X. Райфа [65], причем содержательная сторона данной проблемы занимает в работе главное место.
Наиболее яркими представителями, развивающими теорию игр в ее связи с экономической теорией, следует считать Р. Аумана, С. Карлина, О.Н. Бондарева, Н.Н. Воробьева, В.П. Пацюкова, Г.Н. Дюбина и В.Г. Суздаля, И. Резенмюллера.
Общее определение игры, сформулированное в [27] основано на понятии конфликта, которое также применимо к рассмотрению конкуренции.
Содержательно конфликт естественно понимать как явление, применительно к которому оказываются осмысленными вопросы о том, кто и как в этом явлении участвует, какие у этого явления могут быть исходы, а также кто и как в этих исходах заинтересован. Поэтому в математической модели конфликта должны быть отражены следующие факторы:
- 1. В конфликте участвуют те или иные стороны, являющиеся принимающими решение субъектами. В условиях конкурентного взаимодействия - это множество потребителей, с одной стороны, и монополист - с другой.
- 1. Стороны могут образовывать (реально или условно) коалиции, то есть субъект может иметь сложную структуру, но выступать как один элемент, обладающий общим свойством принятия решений.
- 2. Участники конфликта принимают решения, называемые стратегиями.
- 3. Исход конфликта определяется результатом выбора всеми субъектами стратегий и называется ситуацией или состоянием игры.
- 4. Для каждой коалиции на множестве всех ситуаций игры должно быть задано бинарное отношение предпочтения.
Так же в [27] приведена классификация существующих классов игр. Основным аспектом данного определения является указание общих особенностей взаимодействия элементов - игроков, позволяющих описать его как игровое. Наиболее распространенными классами игр являются:
- 1. Теория матричных игр [27, 86] ни только не предполагает учета и задания сложных форм неопределенности, но и не позволяет рассматривать множество потребителей, как одного игрока, имеющего разветвленную структуру.
- 2. Антагонистические игры [86] предполагают абсолютную противоположность стратегий участников. В случае же монопольной конкуренции потребители в силу своего маленького размера не влияют на рыночную ситуацию. Ее единолично определяет монополист.
- 3. Коалиционные (кооперативных) игры [86, 84, 89] рассматривают вопросы взаимодействия групповых игроков. При монополии потребители могут рассматриваться как коалиция, но действующая без координации своих участников. Монополист представляет собой одного единственного субъекта.
- 4. Рассмотрение взаимодействия монополиста и множества отдельных потребителей, как это реализуется в бескоалиционных играх [83, 48], может привести к существенному усложнению расчетов, если множество потребителей достаточно велико.
- 5. Теория дифференциальных игр [60, 82, 83] применима в том случае, если параметры системы задаются аналитически, т. е. могут быть представлены в виде функций и при условии неизменности структуры игры. При наличии неопределенностей разного рода возникает большое количество ограничений для получения решения, а, следовательно, и на области его применения.
Реализуемость решений игр путем определения множеств стратегий составляет существенную часть теории игр. В теории игр результаты полученного решения сами подлежат дополнительному анализу, который, как правило, затруднителен и требует высокой квалификации аналитика, перерастая порой в самостоятельную задачу [65]. Возникает проблема непосредственной оценки выбора стратегии в конфликтной ситуации, математически описываемой игрой. Следует также отметить, что некоторые виды игр сами еще не до конца проработаны, и их применение на практике должно быть весомо обосновано.
Анализ экономической сущности монопольного рынка показывает возможность отнесения рассматриваемого вида конкуренции сразу к нескольким классам игр.
Базовые положения и понятия данной теории по своей сути очень сочетаются с принципами конкуренции. Подтверждением этого на лингвистическом уровне является то, что во многих источниках понятию «конкуренции» в соответствие ставится синоним «конкурентная борьба», что демонстрирует еще большую применимость теоретико-игровых моделей и подходов.
Приведенные в данном разделе отличия в структуре и характере конкурентного взаимодействия не позволяют применить для построения модели монопольной конкуренции какой-либо один теоретико-игровой подход, а наличие неценовых характеристик товара, имеющих качественное выражение, не позволяет использовать традиционные методы создания математических моделей.
В связи с этим предлагается разработать новую модель, основывающуюся на базовых положениях теории игр, но использующую, в качестве аппарата, положения теории принятия решений.
С точки зрения теоретико-игрового подхода все элементы рынка могут быть названы игроками. Предприятие-монополист M определим, как игрока I. Главной целью игрока I является максимизация прибыли от реализации товара. Предприятия-потребители с позиции монополиста структурно не отличаются. Всем им свойственны одни и те же признаки. Важным является тот факт, что они имеют определенную общность целей, хотя при этом могут быть не связаны друг с другом непосредственно. Эта общность заключается в том, что каждый потребитель желает максимизировать потребительскую выгоду от приобретаемого товара, не имея возможности воздействовать непосредственно на цену. Предлагается, в силу общности целей, считать множество потребителей составным игроком II.
Игровой процесс заключается в следующем. Игрок I предлагает потребителям товар, пытаясь максимизировать прибыль (рис.3.1) за счет увеличения ценовых характеристик товара. Игрок II, сравнивая неценовые характеристики и потребительскую выгоду от них (рис.3.1) с запрошенной ценой, формирует величину потребности в каждом из товаров. Уменьшение потребности в товаре игрока II влияет на величину получаемой прибыли от реализации этого товара игроком I. Так как игрок II имеет составную структуру, то потребность в каждом товаре формируется независимо каждым из потребителей множества PT.
Замечание 3.1. Следует также отметить, что величина потребности в товаре каждого потребителя не связана аналитической зависимостью с ценовыми, и, тем более, с неценовыми характеристиками этого товара.
С позиции теоретико-игрового подхода игровой процесс на рынке R в общей форме можно выразить кортежем [27]:
Г = (I, II, X) , (3.10)
где I - предприятие-монополист или игрок I; II - множество предприятий-потребителей или игрок II; X - выигрыш игры Г.
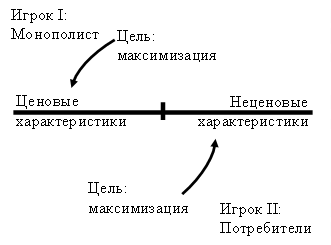
Рис.3.1 Связь интересов игроков и характеристик товара (ценовых и неценовых)
Согласно базовым положениям маркетинга о ценообразовании ценовые и неценовые характеристики связаны. Так улучшение качественных показателей неуклонно ведет к возрастанию цены товара. Минимизация издержек часто не приводит к результатам и в условиях правильно организованной производственной деятельности не всегда возможна.
Выигрыш X представляет собой множество товаров T с заданными характеристиками H, обеспечивающими максимизацию прибыли монополистом и максимизацию потребительской полезности предприятиями-потребителями. Так как товар и его характеристики неразрывно связаны под X будем понимать только H. Данную величину также можно трактовать как стратегию поведения монополиста и потребителей на рынке R.
Формализовано цель монополиста можно выразить:
![]() , (3.11)
, (3.11)
а цель потребителя:
![]() . (3.12)
. (3.12)
В таком характере взаимодействия и заключается важнейшее отличие конкуренции в условиях монополии.
Тогда с учетом (3.10) и сделанных выше замечаний и уточнений игровой процесс на рынке R предлагается выразить кортежем (рис.3.2):
![]() (3.13)
(3.13)
где {hky}опт - выигрыш игры Г, представляющий собой множество оптимальных (устраивающих и монополиста и потребителей) характеристик товара.
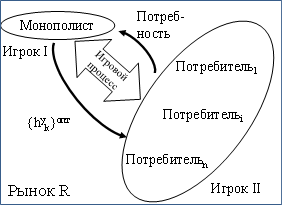
Рис.3.2 Игровой процесс на рынке R
Как видно из (рис.3.1) и (3.11)-(3.12), построить игровую матрицу и применить принцип минимакса (или максимина) в данных условиях нельзя по причине неоднородности вектора характеристик {hky} (3.7) и того, что «объектом интереса» игроков являются разные его части.
Построить и оптимизировать некоторую целевую функцию также нельзя, так как нельзя связать аналитической зависимостью ценовые характеристики важные для монополиста, неценовые параметры важные для потребителей и, например, потребность в товаре потребителя.
Поэтому решение задачи предлагается осуществить в несколько этапов:
- 1. определить целевую аудиторию каждого товара - подмножество потребителей, наиболее сильно влияющих на доход монополиста от реализации каждого товара при неизменном значении потребности;
- 2. выполнить формализацию множества неценовых характеристик товара H, заданных системой качественных оценок;
- 3. определить значения характеристик товара - наиболее соответствующих потребительским запросам игрока II (3.12) и максимизирующих прибыль игрока I (3.11).
