Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Моделирование конкуренции в условиях рынка

Степанов Л. В.,

3.3.3 Модель определения оптимальных характеристик товара

Соперничество порождается ситуацией, когда различие интересов и стремление принимать оптималь­ные решения, приводит к необходимости считаться не только со своими целями, но и с целями других участников рынка, учитывать неиз­вестные заранее решения, которые эти участники будут прини­мать.

В соответствии с (3.13), участниками игры Г являются монополист, как игрок I, с одной стороны, и потребители, как игрок II, с другой.

Для каждой формализованной игры вводятся правила, то есть система условий, определяющая:

• 1. варианты действий игро­ков (стратегии);
• 1. объем информации каждого игрока о поведении партне­ров;
• 2. выигрыш, к которому приводит каждая совокупность дей­ствий.

Стратегией игрока является совокупность правил, опреде­ляющих выбор его действия при каждом личном ходе в зависимо­сти от сложившейся конкрет­ной ситуации, но обеспечивающих достижение его основной цели ((3.11) и (3.12)).

В случае монопольной конкуренции стратегией является набор ценовых и неценовых характеристик каждого товара . Условия монополии приводят к тому, что состав этого набора не меняется и определяется для каждого товара из Т единолично монополистом. Более того, состав шкал для оценки неценовых характеристик (3.25), также можно считать сложившимся и постоянным. Игрок II может только варьировать значения каждой характеристики из заданного набора значений по шкалам.

Данную игру (3.13) следует считать конечной, так как у каждого игрока имеется конечное число страте­гий не более количества товаров. Причем согласно (3.19) число стратегий зависит от того, членом скольких целевых аудиторий потребитель является. Возможен также случай: 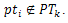. В этой ситуации количество стратегий равно нулю.

Каждый потребитель может быть не полностью информирован о стратегиях и выборе других участников. Условия предлагаемого варианта рассмотрения игрового процесса этого не требуют. Не требует этого и основная цель потребителя (3.12), а также и условия конкуренции.

Как правило, выигрыш может быть задан количественно. Однако, в данном случае, он представляет собой некоторое множество характеристик для каждого товара, устраивающее обоих игроков - монополиста и всех потребителей. Как таковое понятие проигрыша сформулировать для монополистической конкуренции нельзя. Для того, чтобы решить игру (найти решение игры), следует для каждого игрока выбрать стратегию, которая удовле­творяет условиям оптимальности, то есть один из игроков должен по­лучать максимальный выигрыш, когда второй придерживается своей стратегии. В то же время второй игрок должен иметь минимальный проигрыш, если первый придерживается своей стратегии. Такие стратегии называются оптимальными. Оптимальные стратегии должны также удовлетворять условию устойчивости, то есть любому из игроков должно быть невыгодно отказаться от своей стратегии в этой игре. Целью предлагаемой модели является определение единой оптимальной стратегии, устраивающей каждого игрока. При выборе оптимальной стратегии естест­венно предполагать, что оба игрока ведут себя разумно с точки зрения своих интересов и эти интересы не противоречат специфике монопольной конкуренции (определение 12.1).

Предлагается следующий процесс разыгрывания игры Г: игроки I и II, независимо друг от друга, выбирают соответственно некоторые стратегии STRI и STRII, в результате чего складывается некоторая ситуа­ция . После этого рассчитывается выигрыш {h_k^y} ^опт, который и применяется игроком I.

Игрок I на основе анализа собственных производственных возможностей и рынка выбирает некоторую стратегию STRI для k-го товара:

                    (3.37)

При этом эта стратегия учитывает только его собственные интересы (3.11) и возможности.

Другим участником процесса является игрок II, который имеет составной характер.

На основе анализа рыночной ситуации, а также внутреннего состояния каждый pt_i, входящий в состав целевой аудитории  k-го товара формирует свою стратегию:

                       (3.38)

Так как часть характеристик имеет качественное выражение для дальнейшего моделирования игрового процесса, необходимо выполнить формализацию и переход к числовому выражению значений неценовых параметров NC согласно модели (3.23)-(3.33).

В результате формируется вектор, состоящий из набора желаемых характеристик k-го товара всех потребителей (табл.3.4):

Таблица 3.4

Множество желаемых характеристик k-го товара

.                     (3.39)

Согласно (3.13) игрок II имеет составной характер и все его компоненты (потребители) в рамках PT_k равнозначны. Следовательно, необходимо сформировать совокупную стратегию STRII.

Для решения этой проблемы предлагаются два способа.

Способ 1.

Предлагается выполнить усреднение по одинаковым критериям всех характеристик  k-го товара:

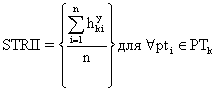,    (3.40)

где h^y_ki - y-я характеристика k-го товара i-го потребителя.

Способ 2.

Приведем значения по различным критериям к одной шкале. Для чего, введем обозначение  - максимальное значение y-го критерия, а  - минимальное значение y-го критерия.

Сформируем матрицу:

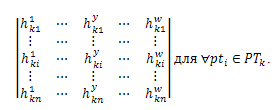.          (3.41)

В случае максимизации критериев (чем больше показатель, тем лучше) из каждого элемента столбца матрицы вычитается минимальный элемент данного столбца и результат делится на разницу между максимальным и минимальным элементами этого столбца:

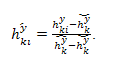.               (3.42)

В случае минимизации критериев (чем меньше показатель, тем лучше), нормализованные оценки равны:

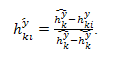.               (3.43)

В результате нормализации, вне зависимости, ведется ли максимизация или минимизация критерия, альтернатива, имеющая наилучший показатель привлекательности по любому критерию получает оценку 1, наименее привлекательная имеет оценку 0, а остальные альтернативы имеют промежуточные оценки от 0 до 1 пропорционально их привлекательности между показателями наилучшей и наихудшей альтернатив.

Для сравнения характеристик предлагается использовать функцию полезности. Согласно [5, 51, 59, 28], любому набору параметров можно поставить в соответствие некоторую количественную оценку данного набора. Значение, которое принимает функция полезности на конкретном наборе параметров, называют полезностью данного набора.

Если критерии обладают равной значимостью, то на основе критерия Лапласа значение функции полезности для каждого потребителя:

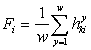 .                      (3.44)

Если критерии обладают различной значимостью, что наиболее вероятно, так как для потребителя наиболее важны неценовые характеристики, то выполняем расчет весов критериев аналогично (3.24) - (3.33).

Затем, значения функции полезности для каждого потребителя вычисляются по формуле с нормализованными показателями привлекательности:

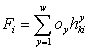 .                      (3.45)

где o_y- веса критериев.

Если известны оценки характеристик товара всех потребителей и решается задача максимизации, то есть, чем выше оценка, тем привлекательнее характеристики, то для принятия оптимального решения выбирают ту альтернативу, для которой функция полезности максимальна. Если решается задача минимизации (чем меньше оценка по критериям, тем привлекательнее), то выбирается альтернатива с меньшей функцией полезности.

Первый способ формирования совокупной стратегии STRII наиболее простой, но не достаточно точный, так как значения отдельных критериев по одному потребителю связаны. Второй способ наиболее соответствует экономическому смыслу выбора совокупной стратегии.

Выбор варианта предлагается осуществлять исходя из следующего. Если нужно наилучшим образом удовлетворить требования к потребительским свойствам товара, по выбор производят путем максимизации. Однако такой вариант более выгоден потребителю, чем монополисту. Если такой задачи не ставится, то используют минимизацию.

В результате формируется стратегия STRII.

Для расчета выигрыша  {h_k^y} ^опт на основе  можно применить один из способов 1 или 2. Этот набор характеристик и реализуется монополистом в производимом    k-м товаре.

Предложенная модель применяется ко всем товарам (3.5) и целевым аудиториям.        В результате получаем множество характеристик H (3.7) рынка R (3.9).

Следует заметить, что полученное множество характеристик H будет учитывать интересы только части потребителей, приносящих монополисту наибольший доход. Для расширения целевых аудиторий можно варьировать значение коэффициента a (3.19) согласно (3.22). Исходя из условий реальных рыночных отношений, могут выбираться и другие значения коэффициента. Однако, расширение аудиторий до охвата всех потребителей приведет не только к увеличению точности принятия решений, но и к возрастанию объема задачи, что может быть не оправдано.

Отклонения в большую сторону от (3.13) для каждого из производителей будет приводить к потере конкурентного преимущества по сравнению с другими участниками рыночных отношений, так как увеличение неценовых характеристик товара будет связано с повышением расходов на производство товаров. Отклонение в меньшую сторону будет приводить к уменьшению целевых аудиторий товаров, то есть к потере потребителей продукции.