Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Моделирование конкуренции в условиях рынка

Степанов Л. В.,

4.2.1 Моделирование ценовой конкуренции

Согласно замечанию 4.1, ценовые характеристики товара имеют количественное выражение.

В силу доступности информации о состоянии рынка, и с учетом (4.11), могут быть собраны исчерпывающие данные о товарах конкурентов. Поэтому для получения преимуществ необходимо определить такие параметры товара, которые бы превосходили другие предложения на рынке. Важно отметить, что конкурентоспособность товара определяется его характеристиками и не зависит от типа и вида конкретного товара.

Обозначим ценовые характеристики товара:

                      (4.13)

где w' - общее число характеристик товара, имеющих количественное выражение; h^Cy - y-я ценовая характеристика товара.

Причем: 

                                            (4.14)            

Таким образом, благодаря информированности участников (условия не информированности характерные для недобросовестной конкуренции, не рассматриваются) рынка монополистической конкуренции о свойствах товаров и услуг можно из количественных характеристик сформировать матрицу  H^c:

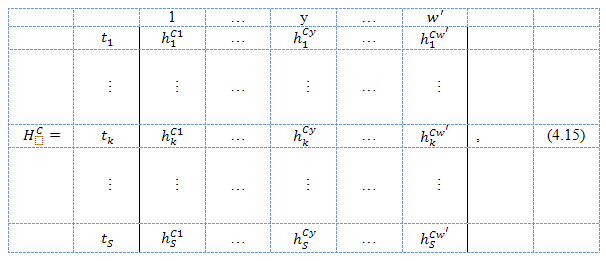
где h_k^Cy - значение y-го количественного параметра k-го товара на рынке R.

Все значения (4.15) определяются на основе спецификации товара и характеризуют его стоимость, внешний вид, форму, размер и так далее, то есть те его параметры, которые заданы в числовой (количественной) форме. Будем полагать h_k^Cy , если y-й параметр у k-го товара на рынке R отсутствует.

В результате  H^c (4.15) представляет собой матрицу количественных характеристик товаров рынка R. С учетом определения 3, для получения конкурентных преимуществ, производитель должен предложить рынку товар по характеристикам опережающий товары других конкурентов. Следовательно, применительно к (4.15) необходимо определить такой вектор характеристик, которые бы обеспечивали конкурентные преимущества предприятию.

В силу большого размера матрицы применение традиционных методов для решения данной задачи неэффективно, так как может требовать существенное время и вычислительные ресурсы. Это делает целесообразным применение адаптированного генетического алгоритма.

Этапы генетического алгоритма:

• 1. Инициализация популяции хромосом.

Исходной популяцией хромосом предлагается считать матрицу характеристик товаров  H^c (4.15). Значения h_k^Cy представляет собой y-ю количественную характеристику          k-го товара на рынке R. Невзирая на то, что все элементы h_k^Cy матрицы H^c имеют численное значение, они выражают различные параметры товара. Шкалы и единицы измерения этих значений могут не совпадать, в то время, как генетический алгоритм может работать только с однородными значениями. Для ликвидации этой неоднородности предлагается произвести нормализацию значений h_k^Cy матрицы H^c.

Определим максимальное значение  y-го критерия:

                           (4.16)

где k - номер товара на рынке.

Определим минимальное значение  y-го критерия:

                            (4.17)

В случае максимизации или минимизации критериев оценки равны:                   

Важно отметить, что минимизация и максимизация может применятся одновременно в рамках одной задачи, но к разным критериям. Также в силу дифференцированности товаров: .

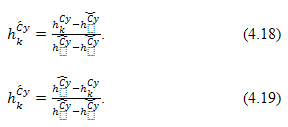
Однако, не все количественные характеристики будут способствовать получению конкурентных преимуществ. Так, например, цена товара, являясь важнейшей характеристикой, при возрастании будет понижать его привлекательность для потребителя. Применительно к условиям ценовой конкуренции, если увеличение характеристики товара позитивно сказывается на его потребительских свойствах, то используется выражение (4.18), в противном случае (например, как с ценой товара) - (4.19).

В результате исходная популяция представляет собой матрицу , состоящую из нормализованных значений характеристик товара.

• 2. Оценка приспособленности хромосом.

Как отмечалось выше, приспособленность характеризует общее «качество» хромосомы. В соответствии с тем, что каждый нормированный параметр товара может оказывать свое определенное влияние на это «качество», необходимо рассмотреть два случая:

• все характеристики товара равнозначны;
• отдельные характеристики товара имеют различное влияние на приспособленность.

В первом случае для расчета значения функции приспособленности хромосомы предлагаем использовать среднегеометрическую или среднеарифметическую зависимость:

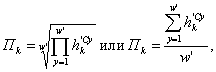                 (4.20)

где h'_k^Cy - нормализованное значение y-й характеристики k-й хромосомы.

Рассчитываемое значение П_k­ будет представлять собой величину, учитывающую равнозначность всех h'_k^Cy.

Во втором случае неравнозначность характеристик может быть задана множеством весовых коэффициентов, учитывающих различное влияние параметров товара. На множестве H^c может быть задано множество оценок характеристик:

                                       (4.21)

где o^y - вес y-й характеристики.

Данный вектор должен формироваться до начала работы генетического алгоритма и в процессе его функционирования не должен пересматриваться.

Тогда, с учетом (4.21) выражение (4.20) примет вид:

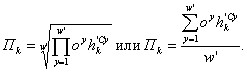                     (4.22)

Среднегеометрическая зависимость обеспечивает большую точность, но может применяться при выполнении условия

Определив значения функции приспособленности (4.20)-(4.22) для каждой хромосомы родительской популяции можно перейти к следующему этапу алгоритма.

• 3. Проверка условия останова алгоритма.

Выбор усло­вия остановки генетического алгоритма зависит от условий решаемой задачи. В данном случае максималь­ное (или минимальное) значение функции приспособленности заранее неизвестно. Нельзя использовать условие отсутствия улучшения решения задачи, а также остановку по истечении определенного времени или числа итераций. С учетом специфики задачи и способа селекции в качестве варианта остановки предлагается рассматривать тот момент, когда в родительском пуле останется одна пара хромосом. При этом осуществляется переход к выбору наилучшей хромосомы. В том случае если данное состояние недостигнуто, выполняется переход к этапу селекции.

• 4. Селекция хромосом.

С позиции генетического алгоритма этап селекции является одним из наиболее важных. Происходит формирование пар хромосом для последующего скрещивания. Для достижения лучшего соответствия разрабатываемой модели процессам в биологических системах, предлагается осуществлять формирование родительского пула на основе применения метода рулетки. Это не противоречит особенностям монополистического конкурентного взаимодействия, так как все участники рынка действуют независимо и могут равновероятно оказывать влияние на других субъектов, с учетом дифференцированности всех товаров.

• 5. Применение генетического оператора скрещивания.

Рекомендации по вариантам осуществления этого этапа были даны выше (п.4.2).              С целью повышения точности предлагается использовать многоточечное скрещивание.

Для каждой хромосомы-потомка рассчитывается новое значение функции приспособленности (4.20) или (4.22).

• 6. Формирование новой популяции.

Стадия формирования новой популяции является завершающим этапом итерации алгоритма. Для реализации запланированного способа останова алгоритма на данной стадии предлагается реализовать вариант естественного отбора по максимуму функции приспособленности:

              (4.23)

В результате популяция потомков сокращается на одну «самую худшую» хромосому и выполняется переход к проверке условия остановки алгоритма.

• 7. Выбор «наилучшей» хромосомы.

При достижении условия остановки генетического алгоритма выбор «наилучшей» хромосомы предлагается осуществлять по максимальному значению ее приспособленности:

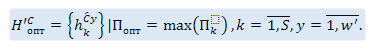                   (4.24)

Эта хромосома представляет собой вектор нормализованных характеристик товара, обеспечивающих конкурентные преимущества предприятию с учетом текущей ситуации на рынке монополистической конкуренции. Для перехода к абсолютным значениям, могут использоваться обратные выражения (4.18) или (4.19) в результате чего получим:

                                    (4.25)

С экономической точки зрения (4.25) представляет собой вектор значений параметров товара (цена, вес, размер и так далее), обеспечивающих предприятию преимущества по сравнению с другими конкурентами.

Важно дополнительно отметить, что благодаря предложенному механизму переноса «непарных» хромосом в новые популяции уменьшается риск потери ценных для алгоритма значений характеристик товара. А за счет применения многоточечного скрещивания в целом возрастает точность всего алгоритма. Кроме того, выполнение естественного отбора на этапе формирования новой популяции является наиболее рациональным и не допускает потери информации на первой итерации генетического алгоритма.

Кроме ценовых параметров, товар в условиях монополистического рынка имеет, не уступающие по значимости, неценовые характеристики. Их определение нуждается в отдельном рассмотрении.