Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Моделирование конкуренции в условиях рынка

Степанов Л. В.,

4.2.2 Модель неценовой конкуренции

Предложенный адаптированный генетический алгоритм и его реализация для ценовых характеристик позволяет определить вектор количественных параметров товара (4.25). Исходные данные для формирования этого вектора носят числовой характер.

Вторым видом характеристик товара являются показатели выраженные качественно. Применить для их непосредственной обработки предложенный алгоритм нельзя. Для решения задачи получения характеристик конкурентоспособного товара его необходимо дополнить.

Обозначим неценовые характеристики товара:

                 (4.26)

где w" - общее число характеристик товара, имеющих качественное выражение;  h^NCy - y-я неценовая характеристика товара.

Неценовая конкуренция является для монополистического рынка унаследованным признаком от монополий (гл.3). В соответствии с определением 17, под качественно определенной величиной следует понимать показа­тель привлекательности товара, выраженный одним или множеством лингвистических конструкций (слово или словосочетание) естественного или искусственного языка, принятого в той или иной предметной области. Например: «марка компании - известная», «Удобство доставки товара - среднее» и так далее.

Причем:

                                           (4.27)

Благодаря информированности участников рынка можно из качественных характеристик сформировать матрицу  H^NC:

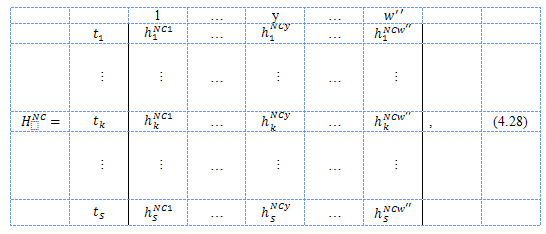
где h_k^NCy - значение y-й качественной характеристики k-го товара на рынке R.

Значения h_k^NCy  в (4.28) определяются экспертным путем, на основе результатов изучения рынка и опроса его участников.

По аналогии с количественными характеристиками будем полагать h_k^NCy = "-", если y-й параметр у k-го товара на рынке R отсутствует у данного товара.

Применительно к (4.28) необходимо определить такой вектор характеристик, которые бы обеспечивали конкурентные преимущества предприятию.

Целесообразность применения адаптированного генетического алгоритма подтверждается теми же обстоятельствами, что и в случае ценовых характеристик. В отличии от (4.15), элементы (4.28) представляют собой лингвистические конструкции, которые не могут использоваться в алгоритме. Поэтому предлагаем следующую технологию решения поставленной задачи на основе применения генетического алгоритма (рис.4.2).

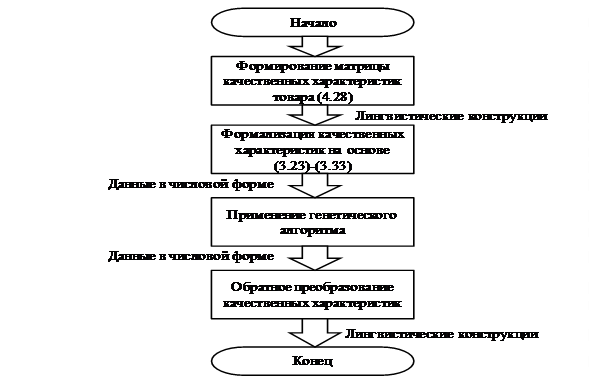
Рис.4.2 Технология применения генетического алгоритма к качественным характеристикам товара

Базовые принципы формализации качественных характеристик рассмотрены выше (п.3.3.2). Применение модели (3.23)-(3.33) позволяет перейти от набора лингвистических конструкции к числовому представлению характеристик. Этот переход обязателен, так как разные параметры могут иметь различный набор терминов, используемых для их характеристики. Переход к числовой форме позволяет их унифицировать.

Следует отметить, что все параметры и переменные генетического алгоритма определяются, исходя из данных выше рекомендаций, и уточнений не требуется.

В результате может быть получена матрица , которую следует рассматривать, как исходную популяцию хромосом. Последующее применение генетического алгоритма (4.20)-(4.24) позволит по достижению условия останова получить вектор оптимальных характеристик:

                 (4.29)

Однако, в отличии от (4.28), элементы вектора (4.29) будет представлены в числовой форме. Для полного завершения генетического алгоритма требуется выполнить обратное преобразование к лингвистическим конструкциям, которое предлагается осуществить на основе шкалы, заданной нормализованными значениями (3.30) или (3.33):

                                                                                (4.30)

Рассмотрим эту процедуру на примере рынка трех товаров. Пусть характеристики этих товаров имеют значения, представленные в таблице 4.2.

Таблица 4.2

Неценовые характеристики товаров рынка R

В соответствии с (3.25) можно задать шкалу важности для всех лингвистических конструкций:

Таблица 4.3

Шкала сравнения

Первым неценовым критерием  h^NC1 является имидж марки компании. Пусть его можно охарактеризовать множеством лингвистических конструкций:

            L¹ = { Известная, Средне, Неизвестная}                            (4.31)

Построим квадратную матрицу (3.26) сравнения лингвистических конструкций:

На основе применения (3.31)-(3.33) вычисляем нормализованные оценки:            

Вторым неценовым критерием  является удобство доставки. Пусть его можно охарактеризовать множеством лингвистических конструкций:

                     L² = {Известная, Средне, Неизвестная}                                (4.34)

Квадратная матрица сравнения лингвистических конструкций:

Нормализованные оценки:            

Третьим критерием h^NCa является качество обслуживания:

                   L³ = {Высокоеб Низкое}                               (4.37)

Квадратная матрица сравнения лингвистических конструкций:

Нормализованные оценки:            

Объединяя базовые положения методов аналитической иерархии [46, 105] и подходы теории нечетких множеств [59, 51] предлагается рассматривать полученные векторы оценок, как некоторые интервальные характеристики. Так, для качественного критерия  значению «Низкое» соответствует интервал [0; 0,125], а значению «Высокое» - (0,125; 1].

Таким образом, полученные векторы (4.33), (4.36) и (4.39) на интервале [0,1] задают некоторую шкалу. Графически полученные нормализованные значения можно представить в виде диаграммы (рис.4.3).

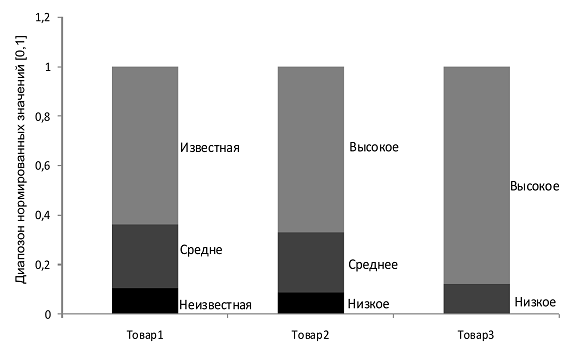
Рис.4.3 Нормализованные оценки лингвистических конструкций

В результате формализованные неценовые характеристики этих товаров имеют значения (табл.4.3):

Таблица 4.3

Формализованные характеристики товаров

Фактические табл.4.3 представляет собой родительскую популяцию хромосом, гены которой представлены в количественной (числовой) форме. Таким образом, предложенный способ формализации лингвистических конструкций позволяет перейти к применению модифицированного генетического алгоритма.

Пусть в результате применения генетического алгоритма был получен вектор оптимальных характеристик:

                   (4.40)

Тогда, согласно рис.4.4 полученному вектору нормализованных значений можно поставить в соответствие фактические значения неценовых характеристик:

                        (4.41)

В результате независимого применения адаптированного генетического алгоритма к ценовым и неценовым параметрам товаров рынка монополистической конкуренции получены два вектора оптимальных характеристик (4.25) и (4.30). Результирующий вектор представляет их объединение:

                                                  (4.42)

Важно отметить, что (4.42) является фактически моделью идеального, с позиции потребительских (ценовых C и неценовых NC) характеристик, товара. Эти характеристики получены с учетом конкурентного взаимодействия, но без учета потребностей субъектов другого сегмента рынка. Любые отклонения от данного эталона будут приводить к потере конкурентоспособности.

Предложенные модели (п.4.2.1) и (п.4.2.2) могут применятся, как для определения конкурентоспособных производимых, так и наиболее желаемых потребляемых товаров. Однако, для получения представления о рыночном процессе требуется определить параметры товара рынка монополистической конкуренции в целом.