
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
5.2.3 Модель при условии чистой олигополии
В условиях чистой олигополии все производители выпускают однородный стандартизованный товар, как и при совершенной конкуренции. Однородность предполагает, что производимые товары имеют одинаковые (по числу и значениям) характеристики. Поэтому в этих условиях соперничество уступает место кооперации, целью которой является распределение количества выпускаемой продукции между производителями для обеспечения потребностей рынка. Это подтверждает возможность предложенного варианта рассмотрения рынка, как двухуровневой структуры. В соответствии с этим, чистую олигополию можно считать конкуренцией, протекающей на виртуальном уровне взаимодействия субъектов рынка, то есть на уровне производителей товаров.
Распределение ресурсов играет важную роль при олигополии. Так, в формах с потерей самостоятельности, также требуется распределять различные ресурсы среди участников образуемого объединения. Это делает актуальным рассмотрение вопросов распределения ресурсов в условиях олигополистической конкуренции.
Определение 18. Коалиция - объединение субъектов рынка для решения общих экономических задач и достижения общих целей.
При решении задачи ресурсного распределения необходимо обеспечить выполнение условия:
![]() (5.26) или
(5.26) или ![]() , (5.27)
, (5.27)
где qjk - количество k-й продукции вменяемой для выпуска j-м производителем коалиции S, причем:
![]() . (5.28)
. (5.28)
При определении (5.26) должны учитываться индивидуальные особенности каждого субъекта prj коалиции S.
Для получения распределения предлагается воспользоваться вектором Шепли [12, 48, 47]. В [89] доказано, что оптимальный вектор распределения Шепли будет единственным для коалиции предприятий.
Вектор Шепли - принцип оптимальности распределения выигрыша между игроками в задачах теории кооперативных игр. Представляет собой распределение, в котором выигрыш каждого игрока равен его среднему вкладу в благосостояние тотальной коалиции при определенном механизме ее формирования. Рассмотрим применение вектора для определения распределения ресурса по предприятиям из S и интерпретацию его основных положений для поставленной задачи.
С помощью вектора Шепли можно получить распределение ресурса по предприятиям данной коалиции S, а условие единственности распределения по элементам prj из S позволяет считать его оптимальным.
Вектор
![]() (5.29)
(5.29)
будем называть распределением D по элементам S, где Ψ - некоторая характеристическая функция.
Шепли [89] были сформулированы базовые аксиомы аналитического способа задания характеристической функции Ψ.
Предлагается следующая интерпретация аксиом Шепли применительно к данному исследованию:
- 1. Симметрия: пусть p - произвольная перестановка элементов коалиции, причем
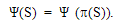 . Тогда
. Тогда 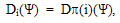 , где через π(i) обозначен образ предприятия при перестановке π.
, где через π(i) обозначен образ предприятия при перестановке π.
Другими словами можно утверждать, что перестановка элементов коалиции приводит к соответствующему изменению множества распределенных значений по его элементам. Данное свойство может быть применено и к множеству производителей, то есть перестановка внутри множества S, составляющих его элементов, приведет к соответствующему изменению вектора Шепли.
- 2. Оптимальность по Парето:
![]() (5.30)
(5.30)
Наиболее важная аксиома. Она определяет то качество вектора Шепли, которое позволяет считать его распределением. Сумма всех составляющих вектора Шепли должна быть равна значению характеристической функции для данной коалиционной структуры.
- 3. Эффективность: если для любого поставщика prjÎS, выполняется равенство
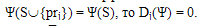
Данная аксиома означает следующее. Если добавляемый поставщик в коалицию не вносит изменения в значения вектора Шепли, то он является незначимым. Добавление незначимых элементов в множества не приводит к изменению распределения, а следовательно излишне. В условиях постановки задачи эта аксиома может использоваться в противоположном качестве. С ее помощью возможно исключение из множества S несущественных элементов. Такое ограничение значительно уменьшает объем и сложность вычислений.
- 4. Агрегация: если характеристическая функция Ψ равна сумме характеристических функций Ψ' и Ψ'', то есть для любой коалиции S справедливо равенство
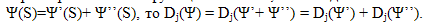
Данное свойство весьма значимо для решаемой задачи. Его смысловым содержанием является тот момент, что часто условия задачи требуют разложения сложных функций на более простые для упрощения решения. Так сложная зависимость элементов коалиции от нескольких факторов может быть учтена получением значений вектора Шепли относительно каждого из них, а затем путем сложения получаем результат их совместного влияния. Необходимо учитывать взаимосвязанность этих факторов, если она отсутствует, то применение аксиомы 4 невозможно.
Тогда, в соответствии с условиями постановки задачи функция D, ставящая в соответствие согласно аксиомам 1 - 4 коалиции S вектор распределения Шепли [48, 89] для данного исследования D = {Dj(Ψ)}, имеет вид:
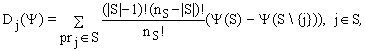 (5.31)
(5.31)
где Ψ(S) - характеристическая функция; nS - количество элементов коалиции S; |S| - переменная суммирования ![]() . Знак модуля в этом случае означает, что величина S используется не как коалиция, а как некоторая целочисленная величина, показывающая количество базовых элементов подмножества S множества производителей.
. Знак модуля в этом случае означает, что величина S используется не как коалиция, а как некоторая целочисленная величина, показывающая количество базовых элементов подмножества S множества производителей.
Для задания характеристической функции Ψ(S) Шепли применялись аналитические формы. Наиболее распространенной является ее задание, как непрерывной функции аналитического вида, либо в качестве распределения вероятностей [12, 47, 89].
Теория кооперативных игр позволяет найти наиболее рациональную с позиции распределения выигрыша коалицию, образованную из множества игроков. Причем поиск осуществляется на основе анализа различных вариантов распределения выигрыша. В условиях же данной задачи коалиция одна и должна быть составлена из всех производителей товара на рынке. Кроме того, при большом числе участников кооперативные игры существенно усложняются. Поэтому данный подход нельзя использовать для поставленной задачи и требуется предложение другого пути ее решения.
Производством называют процесс взаимодействия экономических факторов, завершаемый выпуском какой-либо продукции. При этом, правила, предписывающие определенный порядок взаимодействия экономических факторов составляют технологию данного производства. Ее можно представить, как систему «затраты-выпуск», в которой выпуском является то, что фактически произведено, а затратами - то, что потребляется (капитал, труд, энергия, сырье). Формально можно сказать, что производство - это функция, которая ставит в соответствие набору затрат и заданной технологии, определенный объем выпуска. Конечной целью является получение наибольшей прибыли от реализации своей продукции.
Прибыль представляет собой разность выручки от реализации произведенной продукции и издержек производства, которые представляют собой общий объем выплат за все виды затрат и складываются из двух составляющих: постоянных и переменных издержек. Постоянные издержки фирма несет независимо от объема выпуска (расходы на приобретение оборудования, различные регистрационные сборы и так далее). Переменные - касаются использования имеющихся в распоряжении фирмы факторов производства и изменяются в соответствии с объемом выпуска продукции.
Задача любого предприятия сводится к поиску такого сочетания между затратами факторов производства и выпуском продукции, который обеспечил бы ей наибольшую прибыль. Одним из путей ее решения является минимизация издержек при сохранении заданного объема выпуска продукции. Таким образом, одними из основных факторов, определяющих поведение предприятий, и соответственно, характеризующих предприятия, на рынке являются: выпуск продукции, затраты факторов производства, цены выпуска, цены затрат факторов производства, затраты на совершенствование технологии производства продукции и другие. Как видно из представленного перечня, эти факторы могут быть формализованы и представлены в числовой форме.
Введем обозначение характеристик j-го производителя k-го товара:
![]() (5.32)
(5.32)
где hypri - индивидуальная характеристика pri-го производителя, ![]() - множество характеристик j-го производителя k-го товара.
- множество характеристик j-го производителя k-го товара.
В силу того, что в условиях олигополии на рынке представлены производители однородной продукции, можно утверждать, что по параметрам эти предприятия схожи, то есть имеют одинаковый состав характеристик:
![]() (5.33)
(5.33)
Однако связать между собой некоторые из них и представить в аналитической форме не представляется возможным. В связи с этим для получения значений, характеризующих каждого из участников коалиции, предлагается воспользоваться технологией нейронных сетей [79, 34, 37, 102].
Базовые принципы построения и использования для моделирования рыночных процессов нейросетевых технологий, рассмотренные применительно к условиям совершенной конкуренции требуют уточнения в данной задаче.
Выбор структуры нейронной сети осуществляется в соответствии с особенностями и сложностью задачи. Для решения некоторых отдельных типов задач уже существуют оптимальные конфигурации.
Если же задача не может быть сведена ни к одному из известных типов, разработчику приходится решать сложную проблему синтеза новой конфигурации. При этом он руководствуется несколькими основополагающими принципами:
- 1. возможности сети возрастают с увеличением числа ячеек сети, плотности связей между ними и числом выделенных слоев;
- 2. введение обратных связей наряду с увеличением возможностей сети поднимает вопрос о динамической устойчивости сети;
- 3. сложность алгоритмов функционирования сети (в том числе, например, введение нескольких типов синапсов - возбуждающих, тормозящих и так далее).
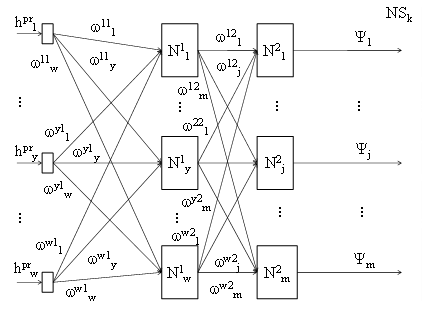
Рис.5.4 Архитектура искусственной нейронной сети k-го товара
Вопрос о необходимых и достаточных свойствах сети для решения того или иного рода задач представляет собой целое направление нейрокомпьютерной науки. В большинстве случаев оптимальный вариант получается на основе интуитивного подбора.
Все указанные принципы способствуют усилению нейронной сети. Однако, основополагающим является соответствие архитектуры сети особенностям решаемой задачи, ее условию и структуре. Другим жестким требованием, предъявляемым архитектурой к элементам сети, является соответствие размерности вектора входных сигналов сети числу ее входов.
Исходя из этих соображений, для моделирования коалиции S производителей предлагается использовать двухслойную архитектуру (рис.5.4).
В предложенной архитектуре входной слой состоит из нейронов, число которых соответствует числу входных характеристик (5.32) j-го производителя. В результате преобразования вектор входных характеристик (5.32) будет преобразован в вектор такой же длины ψ. Процесс преобразования может быть выражен:
ψ=F1(H), (5.34)
где F1 - активационная функция первого слоя.
В случае, когда функция активации одна и та же для всех нейронов сети, сеть называют однородной (гомогенной). Если же активационная функция зависит еще от одного или нескольких параметров, значения которых меняются от нейрона к нейрону, то сеть называют неоднородной (гетерогенной). В условиях данной задачи значения вектора входных параметров являются одинаково значимыми, что позволяет использовать гомогенную структуру. Одной из наиболее распространенных функций является нелинейная функция с насыщением, так называемая логистическая функция или сигмоид [103]. Условия выбора активационной функции рассмотрены ранее (п.п.2.3).
Вектор ψ будет представлять собой совокупность взвешенных характеристических значений вектора исходных параметров. Для применения вектора Шепли (5.30) требуется получить характеристические значения для каждого производителя коалиции. Для решения этой задачи нейронная сеть дополнена вторым слоем (рис.5.4), число нейронов которого равно числу производителей. В результате преобразования получаем:
Ψ=F2(ψ), (5.35)
где F2 - активационная функция второго слоя.
Нейронные сети представляют собой адаптивную систему, жизненный цикл которой состоит из двух независимых фаз - обучения и работы сети. Обучение считается законченным, когда сеть правильно выполняет преобразование на тестовых примерах и дальнейшее обучение не вызывает значительного изменения настраиваемых весовых коэффициентов. Далее сеть выполняет преобразование ранее неизвестных ей данных на основе сформированной ею в процессе обучения нелинейной модели процесса. Сеть успешно работает до тех пор, пока существенно не изменится реальная модель отображаемого явления (например, в случае возникновения ситуации, информация о которой никогда ни предъявлялась сети при обучении). После этого сеть может быть дообучена с учетом новой информации, причем при дообучении предыдущая информация не теряется, а обобщается с вновь поступившей. От качества этапа обучения сети зависит ее способность решать поставленные перед ней проблемы во время эксплуатации. Теория обучения рассматривает три свойства, связанных с обучением: емкость, сложность образцов и вычислительная сложность. Под емкостью понимается, сколько образцов может запомнить сеть и какие функции и границы принятия решений могут быть на ней сформированы. Сложность образцов определяет число обучающих примеров, необходимых для достижения способности сети к обобщению. Важной характеристикой является время, затрачиваемое на обучение. Как правило, время обучения и качество обучения связаны обратной зависимостью и выбирать эти параметры приходится на основе компромисса. Теоретические и практические вопросы обучения искусственной нейронной сети были рассмотрены выше (п.п.2.3).
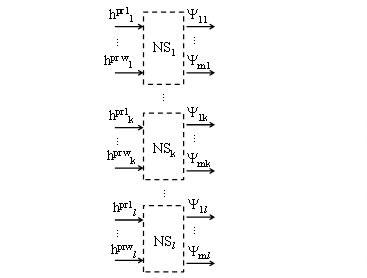
Рис.5.5 Архитектура искусственной нейронной системы коалиции производителей
Производственные характеристики предприятий рынка R зависят от особенностей выпускаемого товара. Эти отличия связаны не только с технологией производства отдельных товаров, но и с экономическими процессами на предприятиях (например, сбытом и хранением). Поэтому использовать одну и ту же нейронную сеть для различных товаров рынка нельзя. В тоже время, определение характеристических значений связано с анализом одних и тех же производственных характеристик, поэтому изменять предложенную архитектуру (рис.5.4) не требуется. Тогда нейронная система коалиции S производителей ранка R может быть представлена совокупностью независимых искусственных нейронных сетей (рис.5.5), количество которых равно числу товаров на рынке R.
В отличие от нейронной системы предложенной выше (гл.2), олигополистический рынок предлагается представить, как нейронную систему только производителей коалиции. Нейронные структуры для потребителей не формируются это связано с незначительностью их влияния на рынок. Основное воздействие на него оказывают только участники коалиции.
В результате предлагается следующая технология использования нейронной системы коалиции S производителей:
- 1. Формирование исходного информационного массива о производственных характеристиках всех производителей коалиции S для всех товаров:

- 2. Последовательная подстановка значений производственных характеристик всех производителей в нейронные сети товаров.
- 3. Формирование промежуточного информационного массива характеристических значений производителей коалиции по товарам:
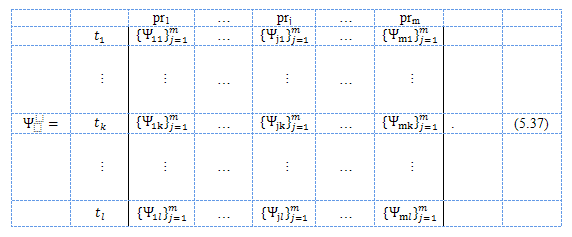
В силу того, что в нейронной сети k-го товара количество нейронов выходного слоя равно числу производителей, подстановка значений характеристик (элементов k-й строки матрицы (5.36)), позволит получить для каждого производителя по каждому товару множество характеристических значений . То есть будут определены характеристические значения каждого производителя, как при собственных параметрах производства, так и при производственных характеристиках всех других участников коалиции. Такой подход позволит имитировать процесс формирования множества коалиций, необходимых для применения вектора Шепли.
- 4. Формирование конечного информационного массива характеристических значений по производителям коалиции:

где ![]() - m-ое число характеристических значений k-го товара j-го производителя.
- m-ое число характеристических значений k-го товара j-го производителя.
Или в развернутой форме для товара tk:
![]() (5.39)
(5.39)
В выражении (5.38) j-й вектор формируется за счет подстановки m раз производственных характеристик tk товара в искусственную нейронную сеть NSk.
Зная (5.38) и используя (5.31), можно получить распределение (5.29), и пропорционально ему определить количество продукции (5.27), вменяемой для выпуска каждым производителем коалиции S.
Следует особо отметить, что новизной предложенного подхода является возможность учета большого спектра производственных характеристик предприятий. Можно учесть не только финансовые показатели производства, но и особенности технологических процессов на предприятиях, а также прочие экономические факторы (маркетинг, сбыт, снабжение, хранение и другие) их деятельности. Возможен и нечеткий вариант описания некоторых показателей. При этом необходимо воспользоваться предложенной в главе 3 методикой формализации нечеткого описания.
