Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Определение оптимального парка воздушных судов.

Припадчев А. Д.,

4.2 Постановка задачи по определению оптимального сочетания авиапарка

Оптимизация это выбор наилучшего варианта из множества возможных [66, 68,136]. Если критерий выбора известен и вариантов немного, то решение может быть найдено путем перебора и сравнения всех вариантов. В нашем случае число возможных вариантов настолько велико, что полный перебор практически невозможен. В этом случае приходится формулировать задачу на языке математики и применять специальные методы поиска оптимального решения, т.е. методы оптимизации [67].

Все задачи оптимизации делятся на два класса:

1) задачи математического программирования, или статические задачи [8, 57, 128];

2) задачи оптимального управления, или динамическими задачами.

Различие между этими классами состоит в том, что в задачи математического программирования необходимо найти оптимальное число, а в задаче оптимального управления оптимальную функцию. С формально-математической точки зрения, это различие существенно, но в нашем, прикладном случае это является условным, и этим различием мы пренебрегаем.

В нашем случае задача заключается в том, чтобы определить наиболее эффективные ВС, но необходимо учесть, что на выбор оптимальных вариантов воздушных судов большое влияние оказывает величина значений параметрического ряда, определить их оптимальное количество, обеспечивающие выполнение объемов пассажирских перевозок в установленные сроки, а также определить для каждого типа ВС наиболее рациональное распределение по маршрутам.

Решение вышеуказанной комплексной задачи должно дать ответ на следующие вопросы:

1) какие типы ВС необходимо применять для заданного объема пассажирских перевозок;

2) на каких маршрутах целесообразно использовать каждый тип ВС;

3) какое количество ВС необходимо иметь авиакомпании для выполнения пассажирских перевозок.

В рассматриваемой задаче предполагается, что все пассажирские перевозки выполняются в полном объеме, со 100 % загрузкой и с установленной регулярностью полетов. Предположим что, необходимо из определенного пункта «А» произвести воздушную перевозку по «п» маршрутам, в соответствии с рисунком 4.2.

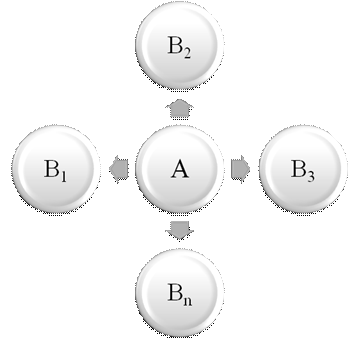
Рисунок 4.2 - Схема авиаперевозок

Предполагаем, что обслуживают эти маршруты следующие типы воздушных судов

1,2,...M,                                    (4.1)

где M - тип воздушного судна.

Предположим, что известно количество авиапассажиров, которых необходимо перевести по каждому маршруту за определенный промежуток времени, за неделю, за месяц и т.д.

Обозначим это количество перевозимых авиапассажиров как:

b₁ - количество перевозимых авиапассажиров по 1-му маршруту;

b₂ - количество перевозимых авиапассажиров по 2-му маршруту;

b_n - количество перевозимых авиапассажиров по N-му маршруту.

Количество рейсов, совершаемых на 1-ом маршруте воздушными судами первого типа обозначим Х_1,1.

 Количество рейсов, совершаемых на 2-ом маршруте воздушными судами первого типа обозначим Х_1,2.

Соответственно количество рейсов, совершаемых на I-ом маршруте воздушными судами J-ого типа, обозначим Х_IJ,

где I=1,2,...N, J=1,2,...M.

Количество пассажиров, перевозимых за один рейс на I-ом маршруте воздушными судами J-ого типа, обозначим а_IJ,

где I=1,2,...N, J=1,2,...M.

Расходы на один рейс на I-ом маршруте воздушного судна J-ого типа, обозначим с_IJ,

где I=1,2,...N, J=1,2,...M.

Предположим, что каждый маршрут обслуживают воздушные суда всех марок 1,2,...M. Тогда для первого маршрута количество перевозимых пассажиров вычисляем по формуле

.                    (4.2)

Для второго маршрута количество перевозимых пассажиров вычисляем по формуле

.                       (4.3)

Окончательно для всех маршрутов составляем систему ограничений-равенств

,                    (4.4)

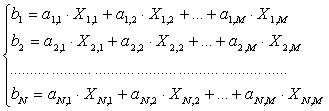
где    а_IJ - известные величины, , ;

b_I - известные величины, ;

Х_IJ - неизвестные величины, , .

Общую сумму расходов на все рейсы всех маршрутов вычисляем по формуле

.                                       (4.5)

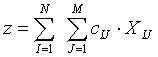
Если необходимо минимизировать общую суммы расходов по формуле (4.5) при выполнении системы ограничений-равенств (4.4), то получаем задачу линейного программирования [13,70, 133].

Задача линейного программирования решается симплекс-методом, т.е. этим методом находят Х_IJ, где ; .

После определения Х_IJ, при , , зная расстояние, скорость, возможно, определить оптимальный парк воздушных судов для узла перевозок «А».

Возможно, к системе ограничений-равенств добавить систему ограничений-равенств (неравенств) по количеству рейсов воздушного судна каждого типа, в результате получаем общее количество рейсов на всех маршрутах воздушных судов типа 1, известное значение, вычисляемое по формуле

.                                            (4.6)

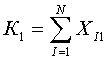
Общее количество рейсов на всех маршрутах воздушных судов типа 2, известное значение, вычисляемое по формуле

.                                            (4.7)

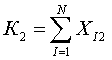
Окончательно систему ограничений равенств по общему количеству рейсов на всех маршрутах для каждого типа воздушного судна вычисляем по формуле

,                                            (4.8)

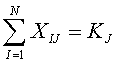
где    .

Добавляя к системе ограничений (4.2) систему ограничений (4.8), возможно, минимизировать общую сумму расходов (4.5). В результате опять получаем задачу линейного программирования, которую решаем симплекс-методом. Для решения необходимо задать b_I, a_IJ, c_IJ, K_J, , .

Для определения рационального использования капиталовложений необходимо провести экономическое обоснование структуры гипотетического парка ВС по авиакомпаниям, их географическому расположению и в целом по стране.

Рост производительности и объем пассажирских перевозок должен опережать стоимость, что является условием эффективного использования каждого нового ВС.