
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.6. Общее и частные положения плоскости в пространстве
Плоскость общего положения
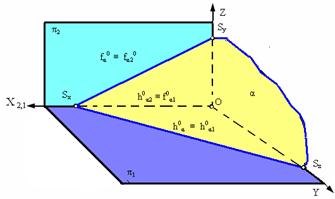
Плоскость, которая занимает произвольное положение по отношению к плоскости проекций (углы наклона этой плоскости к плоскостям проекций - произвольные, но отличные от 0° и 90°) называется плоскостью общего положения (рис. 2.12.а).
На комплексном чертеже следы плоскости общего положения составляют с осью проекций также произвольные углы.
Рассмотрим изображение на комплексном чертеже и свойства плоскостей частного положения: плоскости, перпендикулярные и параллельные плоскостям проекций.
Плоскости, перпендикулярные плоскостям проекций
(проецирующие плоскости)
- 1. Горизонтально-проецирующая плоскость α ┴ π1.
Плоскость α, перпендикулярная горизонтальной плоскости проекции π1, называется горизонтально проецирующей (рис. 2.13).
Основным свойством горизонтально-проецирующей плоскости является то, что любая фигура, расположенная в этой плоскости, проецируется на π1 в прямую линию (горизонтальный след плоскости h0α).
Угол b, который составляет горизонтальный след плоскости h0a c координатной осью Х, равен углу наклона плоскости a к плоскости проекций p2. Фронтальный след такой плоскости перпендикулярен оси Х (f0a ┴ X).
- 2. Фронтально-проецирующая плоскость β ┴ π2.
Плоскость b перпендикулярная фронтальной плоскости проекций π2 называется фронтально проецирующей (рис. 2.14).
а б в
г д е
ж
|
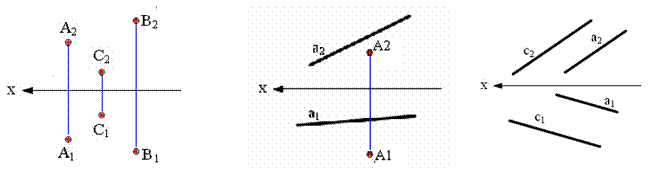
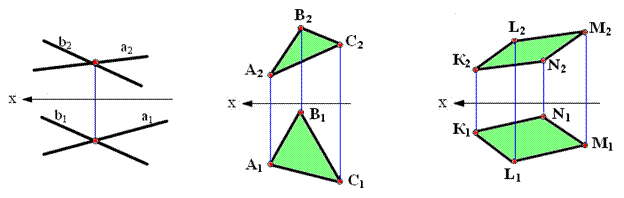
Рис. 2.12. Способы задания
а - тремя точками, не лежащими на одной прямой; б - прямой и точкой вне ее; в - двумя пересекающимися прямыми; г - двумя параллельными прямыми; д,е - плоской фигурой; |
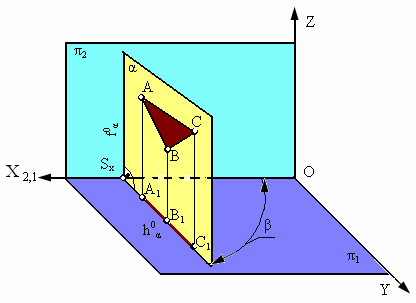
Рис. 2.13. Горизонтально-проецирующая плоскость
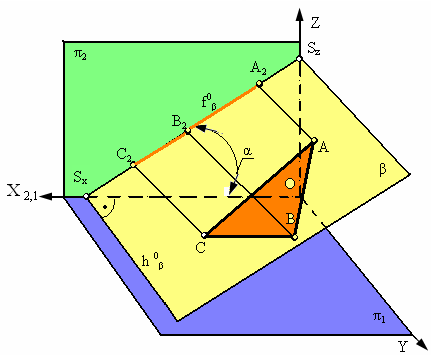
Рис. 2.14. Фронтально-проецирующая плоскость
Основным свойством фронтально-проецирующей плоскости является то, что любая фигура, расположенная в этой плоскости, проецируется на π2 в прямую линию (фронтальный след плоскости f0β). Угол a, который составляет фронтальный след плоскости f0β с координатной осью Х, равен углу наклона плоскости b к плоскости проекций π1. Горизонтальный след такой плоскости перпендикулярен оси Х.
Плоскости, параллельные плоскостям проекций
(плоскости уровня)
1. Горизонтальная плоскость γ || π1.
Плоскость γ, параллельная плоскости π1, называется горизонтальной (рис. 2.15).
Любая фигура, расположенная в такой плоскости, проецируется на горизонтальную плоскость проекций в натуральную величину (Δ А1В1С1 = ΔАВС, рис. 17). Фронтальный след этой плоскости параллелен оси Х (f0g | | Х).
2. Фронтальная плоскость δ | | π2.
Плоскость δ, параллельная плоскости π2, называется фронтальной.
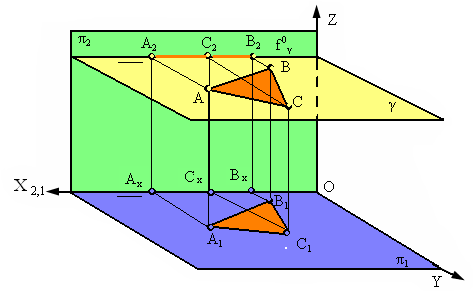
Рис. 2.15. Плоскость, параллельная горизонтальной плоскости проекций
Любая фигура, расположенная в такой плоскости, проецируется на фронтальную плоскость проекций без искажения, т. е. в натуральную величину.
Горизонтальный след фронтальной плоскости параллелен оси Х.
Примечание. Плоскость, параллельная одной из плоскостей проекций, является частным случаем проецирующих плоскостей.
