
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
3.4. Взаимные положения прямых
Две прямые в пространстве могут пересекаться, скрещиваться и могут быть параллельны.
1. Пересекающиеся прямые
Пересекающимися прямыми называются такие прямые, которые имеют одну общую точку.
Из инвариантного свойства 5 следует, что проекция точки пересечения проекций прямых а и b есть точка пересечения этих прямых (рис. 3.4).
2. Параллельные прямые
На рис. 3.5 изображены параллельные прямые - прямые, пересекающиеся в несобственной точке (прямые, лежащие в одной плоскости и пересекающиеся в бесконечно удаленной точке).
Из инвариантного свойства 6 следует, что проекции параллельных прямых а и b параллельны.
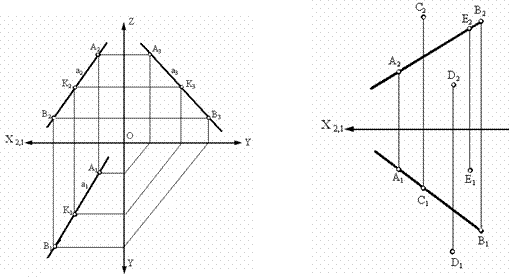
Рис. 3.2. Изображение принадлежности Рис. 3.3. Пример принадлежности
точек А, В, К прямой а точек прямой
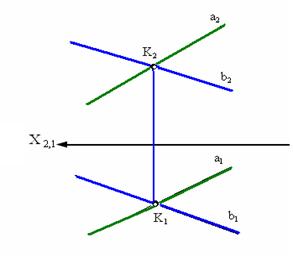
Рис. 3.4. Пересекающиеся прямые
3. Скрещивающиеся прямые
Скрещивающиеся прямые - это прямые, не лежащие в одной плоскости, это прямые не имеющие ни одной общей точки.
На комплексном чертеже (рис. 3.6) точки пересечения проекций этих прямых не лежат на одном перпендикуляре к оси Х (в отличие от пересекающихся прямых, см. рис. 3.4).
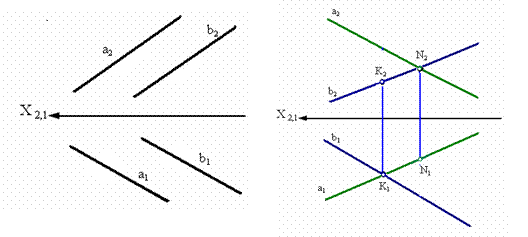
|
Рис. 3.5. Параллельные прямые Рис. 3.6. Скрещивающиеся прямые |
