Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Инженерная графика. Краткий курс

Пиралова О. Ф.,

4.1.Условие перпендикулярности двух прямых на комплексном чертеже

Особый интерес с точки зрения решения задач начертательной геометрии представляют перпендикулярные прямые.

Из классической Евклидовой геометрии известно следующее свойство перпендикулярности двух прямых:

Две прямые перпендикулярны, если угол между ними составляет 90°.

Кроме того, в начертательной геометрии существует еще одно утверждение на эту тему:

Две прямые перпендикулярны, если одна из них линия уровня.

Для подтверждения этого заключения рассмотрим примеры, приведенные на рис. 4.1.

Предположим что необходимо через точку А провести прямую ℓ, пересекающую горизонталь h прямым углом ℓ ┴ h (рис. 4.1.а).

Так как одна из сторон h прямого угла параллельна плоскости π₁, то на эту плоскость прямой угол спроецируется без искажения. Поэтому через горизонтальную проекцию А₁ проведем горизонтальную проекцию искомой прямой ℓ₁┴ h₁. Отметим горизонтальную проекцию точки пересечения прямой и горизонтали M₁= ℓ₁ ∩ h₁. Найдем по принадлежности фронтальную проекцию точки пересечения M₂. Точки А₂ и M₂ определяют фронтальную проекцию искомой прямой ℓ. Две проекции прямой определяют ее положение в пространстве.

Если вместо горизонтали будет задана фронталь f, то геометрические построения по проведению прямой ℓ ┴ f аналогичны рассмотренным с той лишь разницей, что построения неискаженной проекции прямого угла следует начинать с фронтальной проекции (рис. 4.1.б).

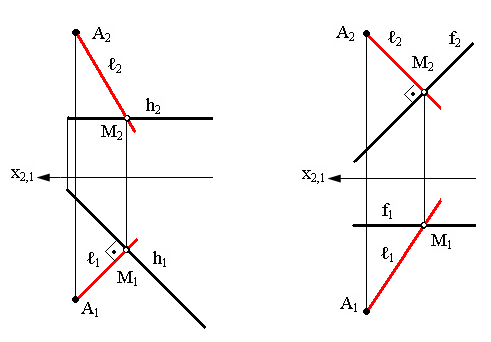
а                                                       б

Рис. 4.1. Примеры построения перпендикулярных прямых:
а) прямая l , перпендикулярна к горизонтали (h); ℓ ┴ h;
б) прямая l, перпендикулярна к фронтали (f); ℓ ┴ f