
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
4.2. Условие перпендикулярности прямой и плоскости
Прямая а перпендикулярна плоскости α, если она перпендикулярна двум пересекающимся прямым b и с этой плоскости.
Если прямые b и с, принадлежащие плоскости α, расположены произвольно относительно плоскостей проекций, то прямые углы между прямой а и прямыми b и с спроецируются на плоскость проекций с искажениями.
Для того чтобы эти прямые углы спроецировались в натуральную величину, прямые b и с должны быть параллельны плоскостям проекций, т. е. являться соответственно горизонталью и фронталью плоскости α..
Прямая а перпендикулярна плоскости α, если она перпендикулярна пересекающимся горизонтали (h) и фронтали (f) этой плоскости.
При этом прямые углы между прямой а и прямыми h и f на соответствующие плоскости проекций спроецируются без искажений.
Кроме вышесказанного существует теорема:
Для того чтобы прямая в пространстве была перпендикулярна плоскости, необходимо и достаточно, чтобы на эпюре горизонтальная проекция прямой была перпендикулярна к горизонтальной проекции горизонтали плоскости, а фронтальная проекция - к фронтальной проекции фронтали этой плоскости.
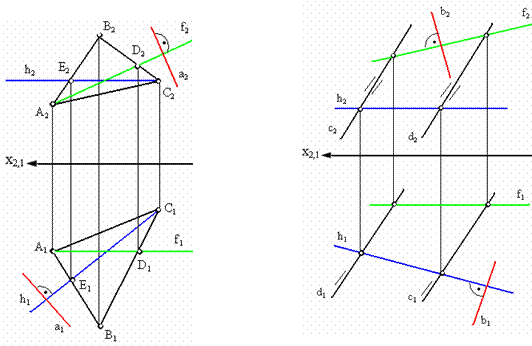
а б
Рис. 4.2. Изображение прямых, перпендикулярных к плоскостям заданным:
а - плоскостью фигуры АВС; б - прямыми c, d
Следовательно, прямая а перпендикулярна плоскости α, если ее проекции перпендикулярны соответствующим проекциям горизонтали h и фронтали f этой плоскости.
На рис. 4.2 изображены прямые а, b, c перпендикулярные плоскостям, заданным различными способами.
Если плоскость задана следами, то горизонталью и фронталью плоскости являются ее пересекающиеся следы.
Следовательно, прямая а перпендикулярна плоскости α, если ее проекции перпендикулярны соответствующим пересекающимся следам плоскости
(рис. 4.3).
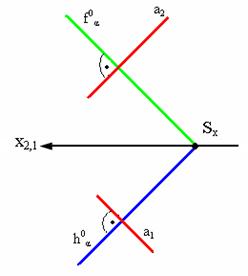
Рис.4.3. Изображение прямой а перпендикулярной к плоскости,
заданной следами
