Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Инженерная графика. Краткий курс

Пиралова О. Ф.,

6.2. Задачи на определение расстояний между геометрическими фигурами

Искомое расстояние во всех задачах этой группы измеряется длиной отрезка, заключенного между заданными геометрическими фигурами и перпендикулярного к одной из них или одновременно к обеим. Этот отрезок проецируется в конгруэнтный ему отрезок на плоскость проекций, которая будет перпендикулярна одной или обеим геометрическим фигурам, между которыми определяется расстояние. Алгоритм решения задач этой группы будет следующим:

1. Одним из способов преобразования комплексного чертежа привести обе заданные геометрические фигуры (или одну из них) в положение, перпендикулярное какой-либо плоскости проекций.

2. Построить проекцию искомого отрезка на эту плоскость. Выбирая способ преобразования комплексного чертежа при составлении алгоритма, следует учитывать требования к компактности чертежа, четкость и возможную простоту графических операций.

Задача 1 . Определение расстояния от точки М до прямой АВ общего положения (рис. 6.1).

Искомое расстояние измеряется длиной отрезка /МN/ перпендикуляра, опущенного из точки М на прямую АВ. Отрезок [МN] спроецируется в конгруэнтный ему отрезок на плоскость проекций, перпендикулярную прямой АВ. Составляем алгоритм решения:

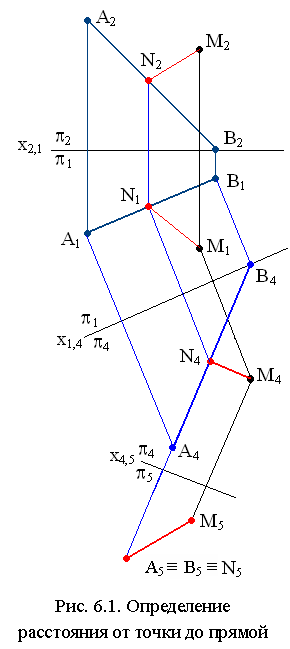
1. Преобразовать прямую АВ в проецирующую прямую способом замены плоскостей проекций.

2. Построить проекцию отрезка [МN] на плоскость П₅ ┴АВ, длина которого М₅N₅ определяет искомое расстояние.

Построение. Для преобразования прямой АВ общего положения в проецирующую выполнены две последовательные замены плоскостей проекций: вначале прямая АВ преобразована в линию уровня, затем линия уровня преобразована в проецирующую прямую. Построены проекций М₄ и М₅ точки М в системе П₄/П₅.

Отрезок [М₅N₅] является искомым: [М₅N₅] ≅ [МN] и /М₅N₅/ = /МN/.На рис. 6.1 показано построение проекций [М₄N₄], [М₁N₁] и [М₂М₂] отрезка [МN] обратным преобразованием.

Задача 2. Определить расстояние между параллельными прямыми а и b.

Для решения задачи необходимо выполнить две замены плоскостей проекций. Вначале прямые a и b необходимо сделать прямыми уровня. Для этого П₄ необходимо расположить параллельно a₁ и b_1. Затем названные прямые необходимо расположить перпендикулярно П_5. Расстояние между а₅ и b₅ будет натуральной величиной между параллельными прямыми a и b (рис. 6.2).

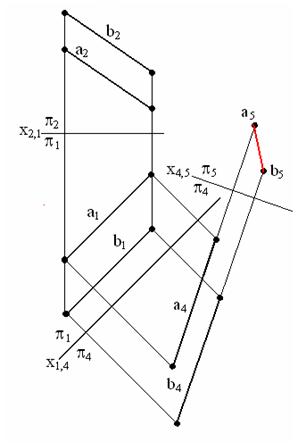
Рис. 6.2. Определение расстояния между параллельными прямыми

Задача 3. Определение расстояния от точки до плоскости.

Решение задачи приведено на рис. 6.3.

Для определения расстояния от точки М до плоскости треугольника ∆АВС необходимо плоскость треугольника общего положения ∆АВС преобразовать в плоскость проецирующую. Для этого нужно произвести замену плоскости проекций П₂ на П₄ перпендикулярно h_1.

Плоскость ∆АВС преобразуется в линию С₄А₄В₄. На эту же плоскость П₄ спроецируется точка М (М₄). Перпендикуляр из М₄ на линию С₄А₄В₄ будет натуральной величиной расстояния от точки М до плоскости ∆АВС. Проекции перпендикуляра переносятся в плоскости проекций П₁ и П₂ по соответствующим линиям связи, расстояния от точки М до плоскости ∆АВС. Проекции перпендикуляра переносятся в плоскости проекций П₁ и П₂ по соответствующим линиям связи.

Примечания: 1) Проекция перпендикуляра М₁N₁ в П₁ располагается параллельно П₄, потому что в плоскости П₄ имеется ее натуральная величина.

2) Задачи 1- 3 можно также решать по следующей схеме: вначале определить метрически искаженные проекции искомого отрезка, а затем способом прямоугольного треугольника определить его действительную величину.

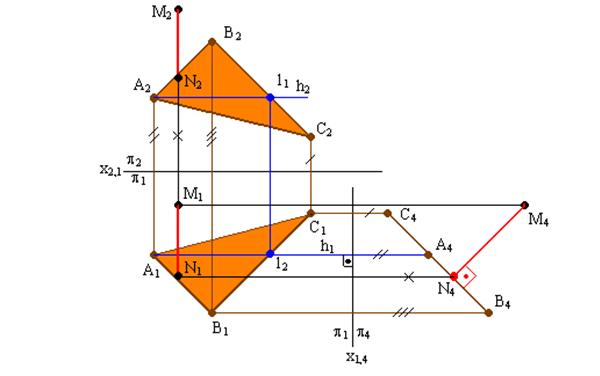
Рис. 6.3. Определение расстояния от точки до плоскости