Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Арютов Б. А., Важенин А. Н., Пасин А. В.,
2.4. Локальная модель производственного процесса в растениеводстве
В связи с глубоком реформированием современного сельского хозяйства возникла потребность в изыскании и разработке новых методологических принципов синтезирования машинных агротехнологических и технических средств для их реализации.
В основу структуры новой методологии может быть положен дедуктивно-индуктивный метод познания объективной реальности, т.е. возможно получить оптимальное решение, двигаясь по пути получения требуемой информации от общих предпосылок к частным или от частных к общим. Ее отличительные признаки: первичность социального заказа, определяющего общую цель и направленность поиска, масштаб конечной задачи и категорию основного заказчика; иерархическая последовательность экспертно-логических и расчетных операций по выбору наилучших решений с итеративно-шаговой их оптимизацией (отказ от концепции однопараметрического оптимума на поверхности монофункционала); приоритет агротехнических требований на технологию и технику по данным исследований агрономических институтов, станций и т.п. организаций; адаптивность технологий и технических средств; маркетинговые исследования при оценке потребности в технике и ее коммерческих характеристик; разработка, создание, освоение производства и организация службы эксплуатации новой техники, рассматриваемые как единый производственный замкнутый процесс в течение периода времени, заданного социальным заказом.
Состояние производственного процесса в различных условиях его функционирования можно описать многомерной переменной 
, которая определяет координаты точки в пространстве технико-технологических параметров. Величины 
не могут принимать любые значения. Выбирая из допустимого множества X (пространства решений) наилучшее по критериям оптимальности 
решение мы, таким образом, имеем возможность оптимального управления производственным процессом в складывающихся погодно-производственных ситуациях.
Если величины могут изменяться непрерывно, т.е. принимают бесконечное множество значений, то допустимое множество будет бесконечным множеством. Однако и в этом случае значения не могут быть какими угодно. На них накладываются ограничения, которые имеют вид алгебраических уравнений или неравенств:
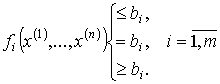, (2.8)
Величины m и n между собой не связаны, так что m может быть больше, меньше или равно n. Переменные не могут быть отрицательными по своему физическому смыслу, т.е. 
.
Состояние производственного процесса не только зависит от переменной x, которая доступна измерению и контролю, но и от множества неконтролируемых или не полностью контролируемых условий его функционирования, которые в значительной мере определяются складывающимися погодно-производственными ситуациями (возмущениями). Полная совокупность таких такого рода возмущений называется в кибернетической терминологии состоянием природы.
Путем некоторой идеализации реальных явлений можно свести все бесконечное многообразие внешних условий к конечному числу возможных состояний природы 
, т.е. ввести в рассмотрение конечное множество 
, называемое пространством состояний природы. Элементы 
множества 
в общем случае являются многомерными величинами 
.
Невозможность полного контроля всех внешних факторов приводит к тому, что вместо точного знания состояния природы 
приходится ограничиваться лишь знанием вероятностей 
различных состояний природы 
. Вероятности , полученные тем или иным путем для всех до начала решения задачи оптимизации технико-технологических параметров производственных процессов в растениеводстве являются априорными.
Для описания целенаправленного воздействия на производственный процесс введем переменную 
, называемую управляющим воздействием или управлением.
Производственный процесс - сложный объект, поэтому приходится использовать несколько управляющих воздействий 
, так что управление представляет собой многомерную величину 
. Управляющие воздействия 
не могут быть взяты какими угодно, а подвержены различного рода ограничениям. Обозначим через U множество всех значений управления u, которые удовлетворяют поставленным ограничениям. При этом любое 
будет допустимым управлением и множество допустимых управлений U является конечным множеством 
.
Судить о том, насколько примененное управление обеспечивает достижение поставленных целей, можно по значениям переменных состояния x. Под действием управляющих воздействий производственный процесс изменяет свои технико-технологические параметры. Характер происходящих при этом процессов определяется скоростью (темпом) изменения переменной состояния 
, которая представляет собой многомерную величину
, (2.9)
где 
- скорости изменения компонент многомерной переменной x.
В производственных процессах растениеводства физические процессы протекают непрерывно во времени, поэтому скорости 
в какой-либо момент времени зависят от состояния объекта исследования в тот же момент времени, который в свою очередь определяется значениями переменной состояния x, состояния природы и принимаемых решений u. Эту зависимость можно записать в виде системы обыкновенных дифференциальных уравнений
, (2.10)
где 
- начальное состояние производственного процесса.
Входящие в уравнение (2.10) переменные x(t), u(t) и 
являются многомерными, т.е. векторными величинами. При этом q - нелинейная функция, описывающая два вида подсистем: структурные и функциональные [4, 27, 29, 54, 64, 66, 67, 217, 218 и др.].