
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.7. Диалоговая система постановки и решения задачи структурной оптимизации производственных процессов в условиях растениеводства
В настоящее время чрезвычайно возросли сложность и комплексность проблем, требующих решения в процессе оптимизации производственных процессов в растениеводстве при различных условиях их функционирования. Создание производственных процессов качественно нового уровня предполагает использование важнейших достижений фундаментальных наук, учет современных экономических, социальных и экологических и других проблем. Задачи повышения качества производственных процессов следует решать на стадии их проектирования, когда необходимо и возможно всестороннее рассмотрение моделей, т.е. должно быть учтено большое число часто противоречивыx требований. Так, в каждой модели могут удовлетворяться такие требования, как минимальная металлоемкость и достаточная надежность, максимальная производительность и минимальная динамическая нагруженность, малая стоимость и другие, т.е. при оптимизации технико-технологических параметров производственных процессов в растениеводстве при различных условиях их функционирования должен быть осуществлен выбор их оптимальных параметров (структурных, кинематических, динамических, эксплуатационных и др.), наилучшим образом соответствующих предъявляемым к ним многочисленным требованиям. Эту задачу при существующей практике проектирования решают, прорабатывая несколько альтернативных вариантов с выполнением соответствующих расчетов. Разработка даже очень большого числа альтернативных вариантов, основанная на традиционных подходах, принципиально не может дать инженеру представления о возможностях производства, так как, например, если придать каждому из 10 параметров по 10 различных значений, пришлось бы рассмотреть 1010 вариантов - задача сложная даже для современных компьютеров.
Затраты на решение задач традиционными методами непрерывно увеличиваются, а отрицательные последствия принятия неоптимальных решений становятся все серьезнее. Осложняющим обстоятельством является то, что такие задачи - многокритериальные с противоречивыми целевыми функциями, поэтому инженеру трудно выбрать обоснованное компромиссное решение: применяющиеся классические методы отыскивания экстремумов и большинство новых поисковых методов оптимизации предназначены лишь для решения однокритериальных задач. Для успешного решения многокритериальной задачи необходимо обоснованное определение допустимого множества решений (областей изменения вектора параметров проектируемой системы). Разработка эскизного проекта производственного процесса может быть осуществлена любым традиционным методом. После разработки эскизного проекта исследователь может определять и назначать пределы изменения каждого из технико-технологических параметров, от которых зависит эффективность производственного процесса в растениеводстве. Должны быть сформулированы критерии - характеристики, по которым можно в ходе проектирования судить о качестве производственного процесса. Такими характеристиками могут быть эксплуатационные затраты, производительность, расход топлива, затраты труда и др. Число критериев качества, которые могут быть проанализированы в процессе проектирования и исследования, методикой выбора оптимальных параметров не ограничено, что очень важно для создания качественного производственного процесса.
Для выбора оптимальных технико-технологических параметров производственного процесса в растениеводстве необходимы расчетные формулы или готовая программа, описывающие поведение исследуемого объекта и позволяющие для любого заданного набора параметров рассчитывать проектируемую систему и вычислять все критерии качества.
Производственные процессы в растениеводстве работают в динамических, интенсивных режимах. Это связано с увеличением быстроходности и снижением массы современных машин, случайным характером изменения сил сопротивления от технологической нагрузки и другими факторами. В связи с этим при решении задач оптимального проектирования производственные процессы в растениеводстве следует рассматривать как колебательные системы, работающие в условиях упорядоченного или случайного возбуждения. Поэтому особое значение приобретает исследование условий их функционирования.
Для объектов современных производственных процессов в растениеводстве, работающих в динамических режимах, на основе дальнейшего развития теории нелинейной механики в последние годы разработаны методы исследования пространственной устойчивости.
Критерии качества вычисляются с использованием методов и программ для заданных параметров объекта [221, 222, 223]. Каждый такой расчет условно назван испытанием. Выбор пробных точек в многомерном пространстве параметров производят с помощью равномерно распределенных ![]() - последовательностей, отличающихся наилучшими свойствами равномерности и позволяющих при минимальном числе испытаний получать достаточно полное представление о ресурсных возможностях моделей по каждому критерию качества [222]. В этом случае пробные точки обладают тем свойством, что проекции их на любую координатную ось в пространстве параметров различны и расположены квазиравномерно. Используя N пробных точек, каждому из параметров придают N значений различных и равномерно расположенных во всем диапазоне изменения параметров. Таким образом, число пробных значений для каждого параметра равно числу испытаний. Разработанный метод выбора пробных точек обеспечивает равномерный обзор всего пространства параметров при сравнительно небольшом числе испытаний, а следовательно, и эффективность метода [221, 222].
- последовательностей, отличающихся наилучшими свойствами равномерности и позволяющих при минимальном числе испытаний получать достаточно полное представление о ресурсных возможностях моделей по каждому критерию качества [222]. В этом случае пробные точки обладают тем свойством, что проекции их на любую координатную ось в пространстве параметров различны и расположены квазиравномерно. Используя N пробных точек, каждому из параметров придают N значений различных и равномерно расположенных во всем диапазоне изменения параметров. Таким образом, число пробных значений для каждого параметра равно числу испытаний. Разработанный метод выбора пробных точек обеспечивает равномерный обзор всего пространства параметров при сравнительно небольшом числе испытаний, а следовательно, и эффективность метода [221, 222].
По значениям каждого строят таблицы испытаний, в которых критерии качества располагают в порядке убывания, т.е. первой стоит лучшая модель по данному критерию. Так как каждой модели соответствует определенный «набор» параметров, зашифрованный в номере испытаний, то из таблиц испытаний видно, что нужно сделать, чтобы получить наилучшую конструкцию производственного процесса по тому или иному критерию качества.
Не существует производственного процесса, оптимального по всем критериям одновременно, поэтому результаты анализа таблиц испытаний используют для обоснования выбора компромиссного решения.
Так как из таблиц испытаний видно, какие возможности имеет конструкция производственного процесса по каждому критерию качества, исследователь может обоснованно назначить такие ограничения по каждому критерию, которые, с одной стороны, были бы практически достижимы, а с другой стороны - удовлетворяли бы требованиям производства. Далее путем расчета проверяют, существуют ли производственные процессы, удовлетворяющие всем этим ограничениям одновременно. Такие конструкции и составляют допустимое множество решений, из которого исследователь совместно с заказчиком выбирает оптимальную модель. Если таких конструкций не оказалось, то ограничения могут быть ослаблены. Возможно также увеличение числа испытаний или расширение границ изменения параметров.
Таким образом, исследователь получил реальную возможность обосновать постановку задачи многокритериальной оптимизации - одновременно учитывать множество противоречивых критериев, что привело к созданию качественно нового метода проектирования производственных процессов в растениеводстве. Другим достоинством метода, делающим его удобным для реального применения, является практическая возможность решения проблемы проектирования больших систем, которые требуют вмешательства исследователя в процесс расчета. Эффективно использовать так называемый режим диалога «исследователь - персональный компьютер». Разработанный метод позволяет увеличить плотность точек в пространстве параметров и этим обеспечить получение более полной информации об исследуемых моделях, если это необходимо. Практически полезной является возможность повторения эксперимента при различных условиях функционирования производственных процессов в растениеводстве по одним и тем же точкам многомерного пространства.
Обобщенный метод постановки и решения задач оптимального проектирования с использованием диалога «человек - компьютер» позволяет следующее:
- учитывать столько критериев качества, сколько необходимо для полного исследования условий функционирования производственных процессов в растениеводстве (с позиций различных противоречивых критериев, таких, как эксплуатационные затраты, производительность, расход топлива, затраты труда и т.п.);
- определить допустимое множество решений;
- обнаружить несущественные критерии, значения которых мало меняются;
- выявить зависимые или, наоборот, противоречивые критерии;
- определить влияние параметрических ограничений на интегральный критерий;
- выделить несущественные по отношению к какому-либо критерию параметры;
- сформировать интегральные критерии и определить на допустимом множестве решений оптимальные параметры проектируемых производственных процессов в растениеводстве.
Проектируемая система зависит от r варьируемых параметров ![]() , ...,
, ..., ![]() , которые являются координатами точки
, которые являются координатами точки ![]() в r- мерном пространстве параметров. Обычно ее координаты входят в дифференциальные или конечные уравнения, описывающие функционирование системы.
в r- мерном пространстве параметров. Обычно ее координаты входят в дифференциальные или конечные уравнения, описывающие функционирование системы.
В общем случае имеются ограничения:
- параметрические
![]() ; (2.47)
; (2.47)
- функциональные
![]() , (2.48)
, (2.48)
где ![]() и
и ![]() - априорно заданные границы изменения параметра
- априорно заданные границы изменения параметра ![]() ;
;
![]() - функциональные ограничения, зависящие от
- функциональные ограничения, зависящие от ![]() ;
;
![]() и
и ![]() - априорно заданные пределы изменения l-го функционального ограничения.
- априорно заданные пределы изменения l-го функционального ограничения.
При решении оптимизационной задачи ![]() ,
, ![]() ,
, ![]() ,
, ![]() не варьируются.
не варьируются.
Кроме ограничений имеются локальные критерии ![]() , зависящие от интегральных кривых.
, зависящие от интегральных кривых.
Определим локальный критерий как числовую характеристику, которая связана с качеством системы монотонной зависимостью. Для определенности будем считать, что все ![]() > 0, и чем меньше значение каждой из функций
> 0, и чем меньше значение каждой из функций ![]() , тем лучше система (при прочих равных условиях).
, тем лучше система (при прочих равных условиях).
Параметрические ограничения (2.47) выделяют в r-мерном пространстве варьируемых параметров параллелепипед ![]() , объем которого
, объем которого 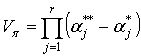 , где
, где ![]() . Функциональные ограничения (2.48) выделяют в
. Функциональные ограничения (2.48) выделяют в ![]() некоторое допустимое подмножество G, которое может быть несвязным, в то время как fl(α) и
некоторое допустимое подмножество G, которое может быть несвязным, в то время как fl(α) и ![]() кусочно-непрерывны. Предполагаем, что объем подмножества G положителен и отношение
кусочно-непрерывны. Предполагаем, что объем подмножества G положителен и отношение 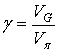 не слишком мало.
не слишком мало.
В качестве решающего критерия ![]() обычно выбирают один из локальных критериев или какую-либо их комбинацию. Тогда легко сформулировать задачу об отыскании наилучших параметров точки
обычно выбирают один из локальных критериев или какую-либо их комбинацию. Тогда легко сформулировать задачу об отыскании наилучших параметров точки ![]() , такой, что
, такой, что 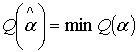 ;
; ![]() . Однако такая постановка чаще всего не приводит к окончательному решению задачи, либо при этом некоторые из критериев не отвечают предъявляемым к ним требованиям. Чтобы избежать такой ситуации, необходимо ввести критериальные ограничения
. Однако такая постановка чаще всего не приводит к окончательному решению задачи, либо при этом некоторые из критериев не отвечают предъявляемым к ним требованиям. Чтобы избежать такой ситуации, необходимо ввести критериальные ограничения
![]() , (2.49)
, (2.49)
где ![]() - худшее допустимое значение критерия
- худшее допустимое значение критерия ![]() .
.
Обозначим через Е множество точек α, удовлетворяющих ограничениям (2.47) - (2.49) так, чтобы ![]() . Если функции fl(α) и
. Если функции fl(α) и ![]() кусочно-непрерывны в
кусочно-непрерывны в ![]() , то подмножества А и Е замкнуты.
, то подмножества А и Е замкнуты.
Назвав параметр Е множеством допустимых точек, можно сформулировать оптимизационную задачу: найти такую точку ![]() , чтобы
, чтобы
![]() . (2.50).
. (2.50).
Если множество Е не пусто, то решение задачи (2.50) существует, при этом ![]() , что исследователя устраивает.
, что исследователя устраивает.
Итак, чтобы от исходных данных перейти к оптимизационной задаче (2.50), необходимо назначить разумные ограничения ![]() и обеспечить непустоту множества Е. Изложенный ниже метод исследования пространства параметров позволяет разрешить эти два вопроса и дает исследователю дополнительную информацию, которая помогает выбрать решающий критерий (решающее правило) Q(α).
и обеспечить непустоту множества Е. Изложенный ниже метод исследования пространства параметров позволяет разрешить эти два вопроса и дает исследователю дополнительную информацию, которая помогает выбрать решающий критерий (решающее правило) Q(α).
Исследование пространства параметров состоит из трех этапов (рис. 2.5).
1 - составление таблиц испытаний. Выбирают N пробных точек ![]() , равномерно расположенных в подмножестве А. В каждой из точек
, равномерно расположенных в подмножестве А. В каждой из точек ![]() вычисляются все локальные критерии
вычисляются все локальные критерии ![]() . По каждому критерию составляется таблица испытаний, в которой значения
. По каждому критерию составляется таблица испытаний, в которой значения ![]() расположены в порядке возрастания
расположены в порядке возрастания
![]() , (2.51)
, (2.51)
где ![]() - номера соответствующих пробных точек (номера испытаний для каждого значения ν) [154].
- номера соответствующих пробных точек (номера испытаний для каждого значения ν) [154].
2 - выбор критериальных ограничений. Рассматривая поочередно каждую из таблиц, составленную в соответствии с зависимостью (2.51), исследователь должен назначить ограничения ![]() . Он заинтересован в уменьшении этих значений, но если выбирать все
. Он заинтересован в уменьшении этих значений, но если выбирать все ![]() слишком малыми, то множество допустимых точек Е может оказаться пустым. Анализ таблиц испытаний проводится для обоснованного выбора решающего критерия
слишком малыми, то множество допустимых точек Е может оказаться пустым. Анализ таблиц испытаний проводится для обоснованного выбора решающего критерия ![]() , так как позволяет учесть не только предварительные указания о роли отдельных критериев
, так как позволяет учесть не только предварительные указания о роли отдельных критериев ![]() , но и их действительные возможности.
, но и их действительные возможности.
3 - проверка разрешимости задачи (2.50). Фиксируют какой-либо из критериев, например ![]() , и рассматривают соответствующую ему таблицу.
, и рассматривают соответствующую ему таблицу.
Пусть ![]() число значений в этой таблице, удовлетворяющих выбранному критериальному ограничению:
число значений в этой таблице, удовлетворяющих выбранному критериальному ограничению:
![]() . (2.52)
. (2.52)

Путем перебора имеющихся значений ![]() при всех значениях ν нетрудно проверить, есть ли среди точек
при всех значениях ν нетрудно проверить, есть ли среди точек ![]() хотя бы одна такая, для которой справедливы одновременно все неравенства (2.49). Если такая точка есть, то множество Е непусто, и задача (2.50) разрешима. В противном случае следует вернуться ко второму этапу и ослабить ограничение
хотя бы одна такая, для которой справедливы одновременно все неравенства (2.49). Если такая точка есть, то множество Е непусто, и задача (2.50) разрешима. В противном случае следует вернуться ко второму этапу и ослабить ограничение ![]() . Если такой шаг крайне нежелателен, то можно вернуться к первому этапу и увеличить число пробных точек, чтобы повторить второй этап с таблицами испытаний большего объема.
. Если такой шаг крайне нежелателен, то можно вернуться к первому этапу и увеличить число пробных точек, чтобы повторить второй этап с таблицами испытаний большего объема.
На первом этапе просматриваются по одной все k строк матрицы ![]() , размер которой
, размер которой ![]() , а на третьем - s столбцов этой матрицы.
, а на третьем - s столбцов этой матрицы.
Для выбора пробных точек используем точки ![]() -последовательности
-последовательности ![]() .
.
Точки α выбирают следующим образом. По декартовым координатам очередной точки ![]() находят декартовые координаты точки
находят декартовые координаты точки ![]() , которая принадлежит
, которая принадлежит ![]() :
:
![]() . (2.53)
. (2.53)
При ![]() рассчитывают проектируемую систему и проверяют условия (2.48). Если они выполнены, то точка
рассчитывают проектируемую систему и проверяют условия (2.48). Если они выполнены, то точка ![]() отбирается в качестве пробной и вычисляются все
отбирается в качестве пробной и вычисляются все ![]() , в противном случае точка
, в противном случае точка ![]() отбрасывается.
отбрасывается.
Выражения вида (2.53) позволяют выбирать критериальные ограничения, ориентируясь на относительную ценность локальных критериев.
На третьем этапе, вообще говоря, находим не одну, а N0 пробных точек, принадлежащих Е, которые могут служить начальными для различных методов локального поиска. Способ построения и отбора этих точек основан на их равномерном распределении в Е.
Анализ таблиц испытаний позволяет обнаружить несущественные критерии, значения которых мало меняются; выявить зависимые или, наоборот, противоречивые критерии; определить влияние параметрических ограничений на интегральный критерий; выделить несущественные по отношению к какому-либо критерию параметры; выделить паретовское множество решений, определить оптимальные параметры. К наиболее важным результатам анализа таблиц испытаний следует отнести получение допустимого множества моделей и определение ресурсных возможностей моделей по всем локальным критериям качества. В большинстве практических задач выбор оптимальных параметров производственного процесса осуществляется только на основании анализа таблиц испытаний, дальнейшие попытки улучшить параметры, как правило, оказывались малоэффективными.
Рассмотренная методика впервые позволила исследователям вводить в рассмотрение столько локальных критериев, сколько необходимо. Такой подход следует считать наиболее правильным и перспективным при рассмотрении сложных многопараметрических и многокритериальных задач комплексного проектирования производственных процессов в растениеводстве.
