Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Методы повышения эффективности механизированных производственных процессов по условиям их функционирования в растениеводстве: Учебное пособие

Арютов Б. А., Важенин А. Н., Пасин А. В.,

2.8. Аналоговая схема параметрической оптимизации производственных процессов в условиях растениеводства

Повышение эффективности производственных процессов растениеводства - важная народнохозяйственная проблема. В настоящее время научные разработки по решению этой проблемы сдерживаются внедрением по ряду причин. Основные из них, на наш взгляд, следующие.

1. Сложность применяемых математических аппаратов.
2. Трудоемкость расчетов при проектировании использования техники.
3. Необходимость иметь большой банк данных, который к тому же должен постоянно обновляться.

Устранению этих причин способствует внедрение в производство автоматизированной системы управления (АСУ). Такие системы успешно функционируют в промышленности и показали высокую эффективность. По существу предлагается переход к автоматизированным технологиям.

Использование автоматизированных технологий в некоторых отраслях промышленности многократно улучшает экономические показатели производства. Эти результаты нередко используют как доказательство необходимости широкой автоматизации и сельского хозяйства. Однако сельское хозяйство обладает многими специфическими особенностями, пренебрежение которыми дает искаженное представление о возможностях автоматизации.

Главная цель сельского хозяйства - производство необходимого количества экологически чистого продовольствия при оптимальных затратах материальных ресурсов. Следовательно, эффективность автоматизации, особенно в условиях рынка, необходимо оценивать степенью снижения себестоимости конечного продукта.

Естественно, что реализация технологий невозможна без широкого использования механизации и автоматизации. Но поскольку автоматизация не цель, а средство, то ее эффективность можно оценить только при рассмотрении всего производства как единой товаропроизводящей системы, в которой автоматизация является лишь вспомогательной подсистемой. Полезность этой подсистемы зависит от характеристик производства, его состояния, совершенства технологии и технических средств.

В условиях рынка главным показателем экономики любого производства является прибыль, которая зависит от цены и объема производимой продукции и от удельных затрат на ее производство. На промышленных предприятиях объем товарной продукции, как правило, определяется производительностью используемых машин, которую можно резко повысить средствами автоматизации (увеличением скоростей, сокращением длительности выполнения технологических операций, введением трехсменной работы оборудования без дополнительного привлечения людей и др.). Поэтому автоматизация промышленных предприятий может многократно улучшить экономику производства.

В растениеводстве все иначе: производителями продукции являются не машины, а биологические объекты (растения), потенциальная продуктивность которых определяется их сортом. Поэтому автоматизация не может ни ускорить сроки созревания биообъектов, ни увеличить их продуктивность. В лучшем случае она может предотвратить снижение потенциальной продуктивности благодаря строгому соблюдению режимов обслуживания биообъектов. Кроме того, большинство технологических процессов в сельскохозяйственном производстве выполняют эпизодически.

Таким образом, в сельском производстве при действующих технологиях автоматизация может только частично улучшить экономику производства, но не радикально (как в промышленности) повысить его показатели.

Существует множество вариантов АСУ, отличающихся рядом признаков: степенью оптимальности, уровнем решаемых задач, необходимыми априорными и текущими информационными обеспечениями, наличием или отсутствием модуля идентификации, поиска, классом алгоритмов оптимизации и др.

При анализе предпочтение отдано системе экстремального регулирования (СЭР). По нашему мнению экстремальные регуляторы в условиях сельскохозяйственного производства наилучшим образом способны к поддержанию на экстремальном уровне показателей функционирования реального объекта, обладающего естественной экстремальной зависимостью указанных показателей от входных величин объекта. При этом характерны априорно неизвестные, относительно медленные трансформации (дрейф) характеристик объекта.

Экстремальный регулятор и объект экстремального регулирования составляют СЭР. СЭР - поисковая система, в которой недостаток априорной информации восполняется за счет текущей, получаемой в виде реакций объекта на искусственно вводимые поисковые воздействия. Она предполагает, что экстремальный выход объекта доступен для непосредственного измерения или вычисляется на основе измерения некоторой совокупности выходных величин. Применительно к решению нашей задачи СЭР имеет отличительную особенность - рассматривается функционал на прогнозируемом движении объекта.

Вектор управляющих воздействий (привлечение дополнительных средств, изменение режима рабочего дня и т. п.) обозначен через u; прогнозируемый вектор возмущений, действующих на объект (свето-, тепло-, влагообеспеченности производства), - через ; вектор состояний объекта (техническая оснащенность, продолжительность выполнения работы и т.п.) - через x. В СЭР входят устройство формирования экстремального показателя (целевой функции Q), устройство организации поиска и орган управления. Устройство организации поиска включает в себя элементы логического действия. В зависимости от изменения Q(t) в результате действия (t) при u(t) оно вырабатывает командные сигналы, поступающие на орган управления, необходимые для приближения системы к экстремальному показателю Q.

,                                  (2.54)

где t - время;

.                                     (2.55)

Существует большое количество достаточно совершенных СЭР, отличающихся по способам поиска экстремума: с запоминанием экстремума, с управлением по градиенту, с измерением производной по времени, шагового типа, со вспомогательной модуляцией и др. Наиболее наглядно действие системы рассматривается на примере одномерной СЭР с сигнум-реле.

С помощью датчика информации о состоянии объекта подается сигнал Q на устройство организации поиска. Последнее устройство состоит из сигнум-реле, реагирующего на знак изменения Q и срабатывающего при переходе изменения Q от увеличения к уменьшению, и устройства логического действия - триггера, изменяющего знак сигнала на обратный при каждом срабатывании сигнум-реле.

При включении системы сигнал и на входе объекта изменяется с постоянной скоростью. Если при этом происходит увеличение Q, то такое движение допускается. В случае, если происходит движение в сторону удаления от экстремума, то Q уменьшается, срабатывает сигнум-реле и триггер - изменяется направление скорости  на обратное. При этом устанавливается движение, соответствующее приближению системы к экстремуму. После прохождения точки экстремума устанавливается режим колебаний системы вокруг экстремума с некоторой амплитудой.

В некоторых системах применяют устройства для их самовыключения после достижения экстремума; причем включение системы в режим поиска происходит или через заданные промежутки времени или осуществляется автоматически при изменении выходной координаты.

При воздействии на выходной сигнал случайных помех для предвычисления статического значения выходного сигнала за малый промежуток времени наблюдения выходной величины целесообразно применить один из методов прогнозирования случайных процессов. Здесь применительно к конкретной структуре СЭР рассматривается метод наименьших квадратов (МНК). Рассматриваемая СЭР включает безинерционное звено с экстремальной характеристикой, последовательное соединение звена с чистым запаздыванием  и трех апериодических звеньев первого порядка с известными времени T₁, T₂ и T₃, на выходе которых действует случайная центрированная помеха  с ограниченной дисперсией.

Тогда связь между выходным сигналом  и входным сигналом  описывается уравнением [224]

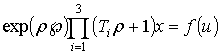,                       (2.56)

где ρ - символ дифференцирования по времени.

Пусть на (k-1) шаге в момент t=0 при начальных условиях , , ,  произведено изменение входного сигнала на . В течение промежутка времени  изменение выходного сигнала будет определяться начальными условиями u₀, x₀, ,  и правой частью . Уравнение, связывающее выходной сигнал x и входной сигнал и системы, будет иметь вид:

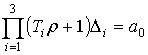,                                 (2.57)

где ; новая переменная  имеет начальные условия .

Решение уравнения (2.57) имеет вид

,                    (2.58)

где

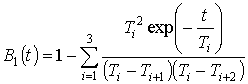,                       (2.59)

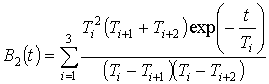,                   (2.60)

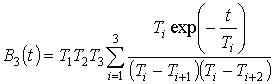.                  (2.61)

При  движение будет определяться уравнением

,        (2.62)

где  - значение выходного сигнала  в момент .

.      (2.63)

Если бы оправдываемость прогноза значений 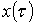 при  была 100%, то для определения параметров , a_i, ,  достаточно было бы иметь переменную  при четырех значениях времени t₁, t₂, t₃, t₄ и решить получающуюся систему четырех уравнений с четырьмя неизвестными. Однако, т.к. прогнозирование производится с определенной достоверностью, рекомендуется иметь значения выходного сигнала в n точках (n>4) и применять МНК (процедуры МНК общеизвестны и здесь не описываются).

Зная оценки a_i и , можно найти за промежуток времени  оценку статического значения выходного сигнала . Для определения правильного направления следующего (k+1) шага выполняем еще одно изменение входного сигнала Δu и отыскиваем аналогичным путем величину . Тогда направление (k+1) шага можно определять из выражения

,            (2.64)

где  C - область значений вектора состояния;

sgn - слоговый символ, означает - знаковая функция.

Это выражение определяет один из алгоритмов ускоренного поиска в СЭР рассмотренного вида при наличии помех, позволяет оптимально достигать главной конечной цели производства (максимума прибыли) на каждом этапе функционирования системы с соблюдением множества ограничений (информационных, вычислительных и др.).

Предлагаемый алгоритм оптимизации технологических процессов растениеводства адекватен релейным методам управления. Релейные методы управления, обладая рядом ценных свойств, состоящих в частности, в том, что они максимизируют область устойчивости системы при ограниченных стабилизирующих воздействиях и минимизируют время перевода системы в окрестность начала координат, имеют следующий недостаток. В окрестности начала координат пространства состояний формирование управления (2.56) приводит к частому переключению управляющего сигнала с одного граничного значения на другое, в результате чего система попадает в вибрационный режим.

С точки зрения надежности системы частые переключения управления - отрицательное явление [27]. Поэтому возникает задача модификации предлагаемой структуры управления технологическими процессами растениеводства таким образом, чтобы устранить виброрежим в окрестности D начала координат и при этом обеспечить близкую к максимальной область притяжения начала координат.

Решение задачи, по нашему мнению, следует искать в классе линейных по x функций. Получающийся в результате закон управления имеет две моды, а именно, для малых x управление формируется по линейной моде c = p(t)x, а для больших x - по релейной (2.56). Система управления будет содержать две структуры - релейную и линейную, обладая при этом свойствами релиона [224].

Задача сводится, во-первых, к определению области D и, во-вторых, к синтезу закона p(t)x. Рассмотрим первую задачу.

Как следует из [229], область D₀, где закон управления определяется только гиперплоскостью p_i(t)x=0, описывается неравенствами

.                         (2.65)

Для устранения виброрежима на гиперплоскости p_i(t)x=0 достаточно выбрать  и .

При построении аналитического критерия перемены структуры целесообразно использовать только линейные операции над вектором x. Поэтому в качестве D следует выбирать ограниченный n-мерный политоп. Указанные выше условия будут выполнены, если область D определять соотношениями

                 (2.66)

и выбрать константу K соответствующим образом.

Пусть η - область виброрежима на той части плоскости p_i(t)x=0, которая принадлежит D. Перейдем к синтезу в D закона p(t)x. Для этого можно использовать какой-либо метод синтеза линейных законов управления. Однако такой подход может не обеспечить достижение цели устранения виброрежима на η. Пусть синтезирован закон p₀(x) и при этом . Строка p₀, естественно, выбирается так, чтобы система была асимптотически устойчивой. Использование закона p₀(x) возможно, пока выполняется условие . Для того, чтобы обеспечить это условие, можно взять какую-либо положительно определенную квадратичную форму V(x), причем  (такая V(x) существует), и найти

,

где .

Тогда областью линейного управления должно быть множество  и виброрежим устраняется в области . Однако при этом условие  не будет выполнено. Множество D будет малой частью области виброрежима, который, по существу, сохранится на плоскости p_i x=0.

В качестве решения второй задачи рассмотрим . Имеем , и  можно рассматривать как непрерывную аппроксимацию в D закона (2.61). Далее, множество η принадлежит внутренности D. Так как в D используется линейный закон управления, то на множестве η виброрежим отсутствует.

Рассмотрим вопрос синтеза алгоритма оптимизации технико-технологических параметров производственных процессов в растениеводстве. Для этого введем переменные z₂(t,x), ..., x_j(t,x), где

                         (2.67)

Над переменными z₂, z₃, ..., z_j можно производить булевские операции, поскольку они принимают только значения 0 и 1. Тогда  только в том случае, если z_j=1 при всех j=2,...,i или , где  - конъюнкция. Итак, если для точки x выполняется равенство , то следует использовать управление . Если же выполняется равенство  или , где - отрицание z_j, то  и принимается управление (2.52). В результате

.

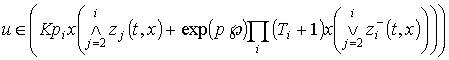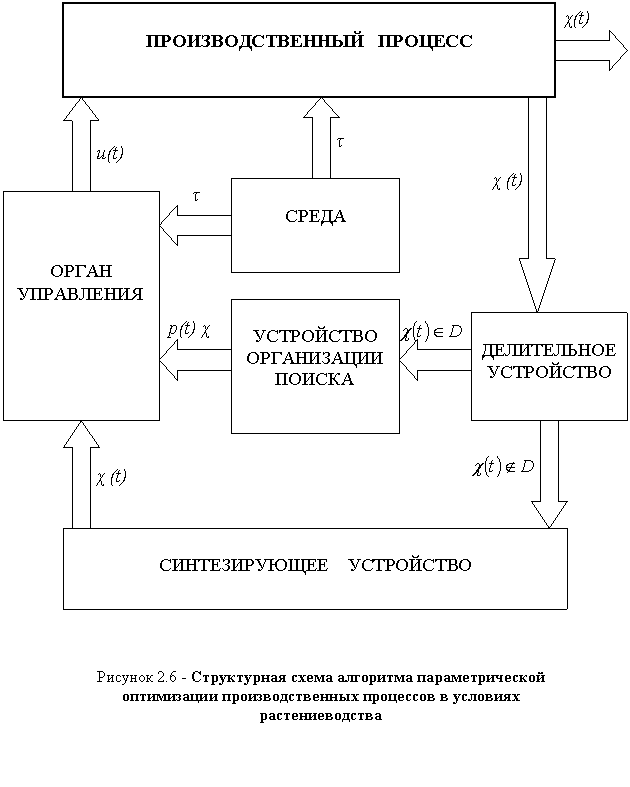
Тогда согласно [226] алгоритм оптимизации технико-технологических параметров производственных процессов в растениеводстве примет вид

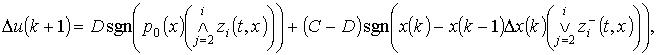
где k - шаг управления.

Данный алгоритм легко реализуется в виде аналоговой схемы
(рис. 2.6). Эта реализация имеет модульную структуру, причем в каждом модуле происходит лишь линейное и релейное преобразование сигналов.