
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
3.1. Задача учета природно-климатических условий при повышении эффективности производственных процессов в растениеводстве
Анализ деятельности сельскохозяйственных предприятий показал, что значительная часть потерь в производстве приходится на биологические потери продукции растениеводства. Невосполнимые биологические потери появляются при нарушении агротехнических сроков работ. Смещение сроков начала работ (до одного месяца) и увеличение их продолжительностей (в 2 ... 5 и более раз) является в значительной мере результатом влияния неблагоприятных погодных условий [27].
М.П. Сергеев, В.Д. Саклаков [9] предлагают учитывать биологические потери урожая при проектировании использования техники в растениеводстве формулой:
![]() , (3.1)
, (3.1)
где ![]() - естественные биологические потери урожая, руб./га;
- естественные биологические потери урожая, руб./га;
и - урожайность, ц/га;
с - цена продукции, руб./ц;
k - коэффициент потерь, 1/сутки;
t - календарная продолжительность работ, сутки.
Однако формула (3.1) не учитывает изменение площади при выполнении работ. Поэтому В.М. Пискарев [142] с целью учета изменения объема работ при увеличении t вводит коэффициент 0,5:
![]() . (3.2)
. (3.2)
Уточнение такого рода, на наш взгляд, приближенно, т.к. в формуле (3.2) отсутствует параметр, характеризующий простои техники по погодным условиям.
Более объективно естественные биологические потери урожая при производстве полевых механизированных работ оцениваются по выражению:
![]() , (3.3)
, (3.3)
где kn - коэффициент погодности (вероятность рабочих дней).
В разности (3.3) вычитаемое - фиктивные потери урожая на площади, где работы выполнены.
Из предлагаемой формулы следует, что при kn = 1 ![]() и при kn = 0
и при kn = 0 ![]() .
.
Иными словами в идеальных погодных условиях производства биологические потери урожая на протяжении t являются величиной постоянной, равной потерям за сутки от биологического оптимума. Однако при прерывании технологического процесса величина ![]() возрастает пропорционально продолжительности простоя по формуле (3.1).
возрастает пропорционально продолжительности простоя по формуле (3.1).
Таким обратом предлагается уточненный подход к учету естественных биологических потерь урожая при проектировании технологических процессов растениеводства (формула (3.3)).
Оптимизацию календарной продолжительности использования техники можно провести по критерию
![]() , (3.4)
, (3.4)
где ![]() - дифференциальные затраты, руб./га;
- дифференциальные затраты, руб./га;
Пn- приведенные затраты, руб./га.
Согласно [149]
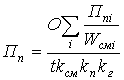 ,
,
где О - объем работ, га;
Пni - приведенные затраты по одному агрегату i звена, руб./га;
Wcмi - нормативная сменная производительность одного агрегата i звена, га/смена;
kcм - коэффициент сменности;
kг - коэффициент готовности.
Однако формула (3.4) с учетом уравнения (3.3) справедлива при многократном прерывании технологического процесса на протяжении его продолжительности. В противном случае функция (3.4) принимает вид гиперболы и не имеет экстремума, т.к. ![]() .
.
Оценим вероятность прерывания технологического процесса в результате ухудшения погоды.
Если коэффициент погодности kn - вероятность работы, то (1- kn) - вероятность простоя по метеоусловиям. Тогда согласно теореме умножения вероятностей вероятность прерывания технологического процесса в результате ухудшения погоды
![]() .
.
Исследование функции p(kn) показывает, что р изменяется от 0 до 0,25 и максимальное значение р = 0,25 при kn = 0,5, т.е. прерывание технологического процесса в результате ухудшения погоды маловероятно, и уравнение (3.4) при оптимизации календарной продолжительности использования техники в растениеводстве не корректно.
Задача оптимизации производственных процессов в растениеводстве при различных условиях их функционирования выходит далеко за рамки уравнения (3.4), является многокритериальной. Решение возможно кибернетическими методами с использованием функций роста сельскохозяйственных культур.
