
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
3.4. Влияние погодных условий на функционирование производственных процессов в растениеводстве
Природно-климатические факторы в сочетании с метеорологическими являются главным ресурсом земледелия. Это основная отличительная особенность сельского хозяйства от всех других сфер производств. Кроме того, по некоторым оценкам, из всех потерь, которые наносят народному хозяйству погодные условия, на долю сельского хозяйства приходится около 65 % [231]. Учитывая уровень развития современной науки около половины указанных потерь предотвратимы путем прогнозирования, планирования и своевременного проведения соответствующих агротехнических мероприятий, дифференцированных по складывающимся условиям.
Прогнозы погоды и агрометеорологические прогнозы имеют существенную разницу, которая определила и степень применимости их в практике планирования сельскохозяйственного производства. Если долгосрочные прогнозы погоды пока еще ниже требований практики сельскохозяйственного производства, а учитываются в планировании средние климатические или типичные для местности и сезона года данные по погоде, то агрометеорологические прогнозы в силу инерционности количественных накоплений влияния в растениях и почве обладают большей достоверностью, удовлетворяющей требованиям планирования.
Широкое распространение агрометеорологические прогнозы получили в практике программирования урожаев, где рекомендуемые мероприятия объединены в целые комплексы.
На разных уровнях агропромышленного комплекса страны метеорологические и агрометеорологическое обеспечение осуществляют Гидрометцентр России, гидрометеорологические бюро, агро- и гидрометстанции. Прогноз облачности, атмосферных осадков, направления и скорости ветра, температуры воздуха и неблагоприятных явлений погоды на сутки и 3 дня составляются к середине текущего дня и передаются по радио, телевидению, публикуются b газетах и гидрометеорологических бюллетенях. Прогнозы средней температуры воздуха на 5 и 10 дней и количества атмосферных осадков на 5 дней публикуются в виде карт полей температуры и осадков, а также в виде описания очагов аномалий температуры воздуха в гидрометеорологическом бюллетене Гидрометцентра России, выпускаемом 12 раз с 5-дневными и 6 раз с 10-дневными прогнозами в месяц.
Прогнозы погоды на месяц издаются Гидрометцентром России в виде брошюры за 25-30 дней до начала месяца с картами полей ожидаемого распределения месячного количества осадков и их отклонений от нормы, нормы и отклонения от норм средней месячной температуры воздуха, а также дается общая характеристика и прогноз погоды по экономическим районам. Сезонные прогнозы по отклонениям от средних многолетних значений температуры воздуха и количества осадков, а также об опасных аномалиях (засухи, избыток осадков), выпускаются Гидрометцентром России шесть раз в год с заблаговременностью 25-30 дней. Кроме того, сезонные прогнозы периодически уточняются и корректируются месячными прогнозами, которые в свою очередь уточняются прогнозами на 10 и 5 дней, а также трехдневными и суточными.
Основными формами агрометеорологического обеспечения являются декадный агрометеорологический бюллетень, обзор «Основные агрометеорологические особенности недели», выпускаемые Гидрометцентром России, а также текущие справки, устные консультации на запросы организаций по различным каналам связи.
Данные о климатических и агроклиматических ресурсах и условиях, различный вспомогательный материал и указания по их практическому использованию содержится в справочниках, атласах и картах, выпущенных в разные годы для различных регионов страны.
Мы не случайно так подробно остановились на доступности информации по прогнозам, ибо необходимость учета метеорологических и агрометеорологических факторов в практике принятия хозяйственных решений ощущается на трех уровнях: 1) при районировании и проектировании производства, в том числе и средств механизации; 2) при планировании агротехнических мероприятий и использования сельскохозяйственной техники и 3) при оперативном управлении работой машинно-тракторного парка и технологическими процессами.
На первом уровне используются среднемноголетние или климатические данные. На втором - месячные и сезонные прогнозы, называемые долгосрочными. И на третьем уровне - суточные (краткосрочные) и 3-, 5-, 10-дневные (среднесрочные) прогнозы.
Оправдываемость (процент совпадения результатов последующих наблюдений, подтверждающих прогноз определенного явления [235]) агрометеорологических прогнозов в силу их инерционности достаточно высока - до 90 % и более. За последние годы оправдываемость краткосрочных и среднесрочных метеорологических прогнозов также повысилась и составила по территории Нечерноземья 88-90 % для краткосрочных и 83- 86 % для среднесрочных. Следует отметить, что из всех прогнозируемых факторов наибольшую оправдываемость имеют прогнозы температуры воздуха. Низка пока оправдываемость долгосрочных прогнозов по комплексу факторов - ниже 70 %, что исключает их учет в деятельности сельскохозяйственных организаций. Хотелось бы обратить особое внимание на оправдываемость сезонных прогнозов температуры воздуха по Европейской части России, которая составила 88 % [231].
Этот факт свидетельствует о том, что из всех факторов долгосрочного прогноза на втором уровне принятия хозяйственных решений, то есть при планировании агротехнических мероприятий и сезонного использования МТП, прогнозы температуры воздуха уже можно учитывать, а тем более сумму среднесуточных температур воздуха, которая обладает инерционностью или определенной «памятью» ретроспективы.
Влияние природно-климатических факторов осуществляется по схеме: природные факторы - предмет труда (растения), почва - средства труда (орудия, машины). В этой цепи наиболее разработанным является звено природные факторы - предмет труда и лишь отдельные исследования [26, 27, 40, 142, 144 и др.] посвящены вопросам зависимости работы машин от метеорологических факторов. Кроме того, все они охватывают в основном вопросы принятия хозяйственных решений на первом и третьем указанных выше уровнях. В то же время вопросы плановой дифференциации использования машинно-тракторного парка по складывающимся условиям эксплуатации лишь в последнее время стали предметом исследований в Прибалтике, Нечерноземье и Сибири.
Предлагаемые ВИМом и другими научными учреждениями коэффициенты погодности, являющиеся пока основным материалом учета природных факторов в механизации сельского хозяйства, разрабатывались по декадам периодов и видам полевых работ на основании средних значений многолетних данных по погоде [40].
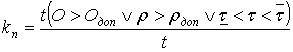 , (3.22)
, (3.22)
где О, Одоп - количество осадков соответственно фактическое и допустимое;
ρ, ρдоп - продуктивная влажность почвы соответственно фактическая и допустимая;
![]() - фактическая температура;
- фактическая температура;
![]() - нижняя допустимая температурная граница;
- нижняя допустимая температурная граница;
![]() - верхняя допустимая температурная граница,
- верхняя допустимая температурная граница,
t - количество календарных дней;
![]() - знак логического сложения, означающий вычет из календарных дней неблагоприятных, когда рассматриваемые параметры выходят за пределы допустимых.
- знак логического сложения, означающий вычет из календарных дней неблагоприятных, когда рассматриваемые параметры выходят за пределы допустимых.
В расчетах по определению рационального состава МТП среднемноголетние значения коэффициентов погодности непременно уточняюще эффективны. Однако в сезонном планировании и оперативном управлении работой МТП они не объективны.
Основываясь на возможности прогнозирования температурных условий и существовании корреляции их с другими метеорологическими факторами, нами предлагается методом расслоения выборок дифференцировать коэффициенты погодности по температурным условиям.
Суть метода расслоения выборки заключается в том, что совокупность из N единиц, разбивается на L подмножеств (слоев) объема Nh, h = 1,2, ..., L таких, когда
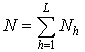 , (3.23)
, (3.23)
то есть совокупность температур каждой декады месяца достаточно большого количества лет разбивается на заранее определенные подмножества (слои) с величиной интервала ![]() не менее, чем доверительный интервал математического ожидания средней декадной температуры одного слоя
не менее, чем доверительный интервал математического ожидания средней декадной температуры одного слоя
![]() ,
,
где ![]() - квантиль нормального распределения;
- квантиль нормального распределения;
![]() - стандарт отклонения.
- стандарт отклонения.
В нашем случае по данным метеорологических наблюдений гидрометстанции Мыза Нижегородской области за 58 лет получилось 5 слоев, характеризующих теплые Х5, умеренно теплые Х4, средние Х3, умеренно холодные X2 и холодные Х1 подмножества температур каждой декады, где
![]() .
.
Для каждой декады по формуле (3.22) определяется коэффициент погодности и как результативный признак в полном соответствии с факториальным он составляет подмножества Y5, Y4, Y3, Y2, Y1. Теперь каждая единица факториального признака и соответствующая ей единица результативного признака будут характеризоваться двумя числами: номером слоя и номером внутри слоя ![]() .
.
Суммарные значения признаков Nh единиц h слоя составляют
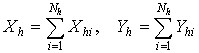 , (3.24)
, (3.24)
а средние значения выразятся
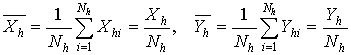 . (3.25)
. (3.25)
Для всей совокупности суммарные и средние значения признаков теперь могут быть определены
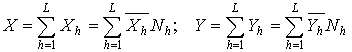 . (3.26)
. (3.26)
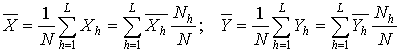 . (3.27)
. (3.27)
Следует доказать, что допускающие содержательную интерпретацию показатели точности факториального и результативного признаков обеспечивают степень точности не менее требуемой. Для этого берется выборка п, аналогично рассчитанная по формулам (3.24), (3.25), (3.26), (3.27) с оценками х, у, ![]() ,
, ![]() в n и хh, yh,
в n и хh, yh, ![]() ,
, ![]() в .
в .
Теперь с помощью обследования п единиц выборки нужно оценить параметры Р и Nh совокупности, то есть целесообразно ли в качестве оценки этих параметров выбрать
![]() , (3.28)
, (3.28)
![]() . (3.29)
. (3.29)
Вероятность того, что дискретная случайная величина примет конкретное значение nh, зависит от объема совокупности N, объема слоя Nh и объема выборки n. Вероятность того, что при заданных N, Nh, и n при отборе без возвращения в выборку объема п попадает nh единиц, обладающих интересующим нас свойством, то есть при гипергеометрическом распределении будет равна
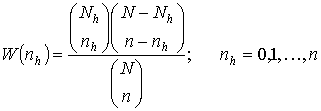 . (3.30)
. (3.30)
Тогда математическое ожидание случайной величины nh определится
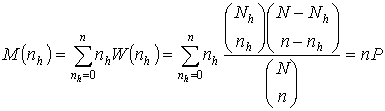 . (3.31)
. (3.31)
Основываясь на свойстве математического ожидания, когда постоянный множитель случайной величины может быть вынесен за знак математического ожидания, можно записать
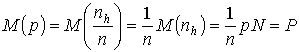 . (3.32)
. (3.32)
Таким образом, доля р в выборке есть несмещенная оценка доли Р в совокупности.
Аналогично
![]() . (3.33)
. (3.33)
Оценка pN есть несмещенная оценка числа Nh.
Если увеличивать объем выборки п, то в пределе получим
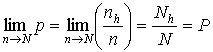 ; (3.34)
; (3.34)
![]()
и при переборе всей совокупности функции оценки (3.28) и (3.29) дают истинные значения искомых параметров Р и , то есть эти функции состоятельны.
Значения р и pN - реализации случайных величин, поэтому в силу (3.30) они принимают частные значения только с определенной вероятностью, а для определения эффективности оценок, то есть количественной характеристики точности оценивания, необходимо знать их стандартные ошибки.
Если при гипергеометрическом распределении M(nh ) = nР, то, используя свойство среднеквадратического отклонения, можно записать
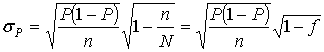 , (3.35)
, (3.35)
где ![]() - доля отбора в совокупности.
- доля отбора в совокупности.
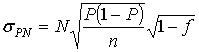 . (3.36)
. (3.36)
Следует здесь отметить также, что при малой доле отбора или при отборе с возвращением стандартная ошибка гипергеометрического распределения переходит в стандартную ошибку биноминального распределения
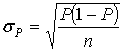 , (3.37)
, (3.37)
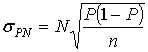 . (3.38)
. (3.38)
Наряду со стандартной ошибкой как средней мерой абсолютного отклонения оценки от ее математического ожидания применяется и относительная стандартная ошибка - коэффициент вариации оценки
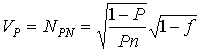 . (3.39)
. (3.39)
Будем полагать, что оценки р и pN для доли Р и числа единиц Nh в слое с интересующим нас свойством нормально распределены. В этом случае можно определить вероятность (1-α ), того, что отклонение оценки от своего математического ожидания не превзойдет определенную величину, выраженную в долях от стандартной ошибки, то есть свою предельную ошибку
![]() . (3.40)
. (3.40)
В нашем случае
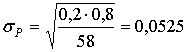
и для ![]() .
.
![]() ;
;
![]() .
.
После некоторых преобразований (3.40) можно показать, что
![]() , (3.41)
, (3.41)
![]() . (3.42)
. (3.42)
Объем выборки п является единственной управляемой в данном случае величиной, которая влияет на стандартную ошибку оценки. По исследованиям [236] оценки имеют приемлемо близкое к нормальному распределение при п >25 и весьма близкое к нормальному при п >57.
Предполагая величины N и Р известными и решая уравнение (3.35) относительно п, после преобразований получаем
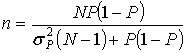 . (3.43)
. (3.43)
При известных относительной и предельной ошибках с использованием уравнения (3.39) получим
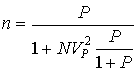 , (3.44)
, (3.44)
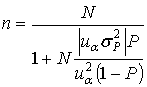 . (3.45)
. (3.45)
В нашем случае возможный объем выборки по формуле (3.43)
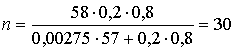 .
.
nh = pn и при Р = р = 0,2 nh = 6.
Таким образом, теоретически доказана возможность проведения дифференциации коэффициентов погодности в соответствии с температурными условиями, которые с достаточной достоверностью могут прогнозироваться при долгосрочном прогнозе.
Проведем обоснование модели учета температуры воздуха при проектировании ситуационного использования сельскохозяйственной техники в растениеводстве.
Объективность при проектировании ситуационного использования сельскохозяйственной техники определяется адекватностью модели реальным процессам.
Математическая модель реального процесса - совокупность точных соотношений между характеристиками этого процесса. Математическое моделирование состоит из двух взаимоувязанных этапов: а) введение абстрактных математических характеристик изучаемого процесса и б) записи строгих соотношений между этими характеристиками, обобщающими интуитивные представления о процессе, почерпнутые из опыта, наблюдения, здравого смысла.
Во всех математических моделях для предсказания развития процесса присутствуют два вида величин: а) внешние, которые в рамках данной модели считаются известными, и б) внутренние, которые вычисляются из соотношений модели при известных начальном состоянии и всех внешних величинах процесса. Деление величин на внешние и внутренние условно и зависит от цели исследования.
В моделях процессов можно выделить три вида внешних величин: а) характеристики данного процесса, б) величины, описывающие влияние на изучаемый процесс некоторых внешних по отношению к нему процессов и в) величины, с помощью которых можно оказывать влияние на процесс, т.е. управляемые. Очевидно, что величины, не являющиеся управляемыми, подлежат экспериментальному определению.
Модель базируется на математических методах, учитывающих инерционность развития рассматриваемых процессов. В основу ее положено изучение систематизированной информации о состоянии и поведении объекта исследования в прошлом, а также выяснение причин определяющих изменение изучаемых процессов в будущем. При этом сущность выдвигаемой гипотезы состоит в том, что будущее является продолжением настоящего с сохранением стабильности существующих тенденций. Необходимо отметить, что рассматриваемые при проектировании ситуационного использования сельскохозяйственной техники факторы имеют ярко выраженный вероятностный характер, что требует использования при разработке прогностической модели аппарата динамической статистики [79].
Для исследования процесса изменения температуры воздуха в течение теплого периода года (с температурой воздуха выше 00С) был проведен статистический анализ массива фактических значений этого фактора за 30 лет по данным метеостанции «Мыза» (центр Нижегородской области). Фактический процесс изменения температуры воздуха в течении времени является нестационарным и неэргодическим.
Для приведения процесса к стационарному виду были устранены нестационарные по математическому ожиданию и дисперсии участки в начале и конце теплого периода года (весна и осень), учет которых не является существенным при рассмотрении механизированных процессов в условиях растениеводства. Оставшуюся часть процесса, стационарную по дисперсии, мы разбили на участки длительностью в 10 календарных суток (декады) и усреднили значения процесса в пределах этих участков. Таким образом была снижена нестационарность процесса по математическому ожиданию.
Неэргодичность процесса, снижавшую возможность получения достоверных вероятно-статистических характеристик, устранили центрированием случайных величин среднедекадной температуры воздуха по средним значениям текущего и среднемноголетнего года. После предварительной обработки массива центрированных среднедекадных значений температуры воздуха мы получили с помощью электронных таблиц EXCEL нормированные корреляционные функции процесса изменения среднедекадной температуры воздуха в период с 3 декады апреля по 2 декаду сентября, центрированные по среднему многолетнему и текущему году (рисунок 3.3).
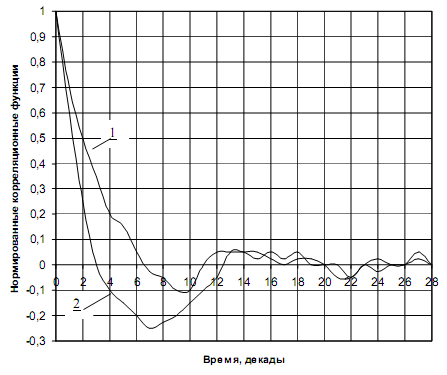
Рисунок 3.3 - Нормированные корреляционные функции процесса изменения среднесуточных температур второй декады июля:
1 - центрированные по средней многолетней декадной температуре;
2 - центрированные по средней текущей декадной температуре
По корреляционным функциям установлено:
1) оценки текущего года более эффективны, чем среднего многолетнего, на интервале времени ![]() больше трех декад;
больше трех декад;
2) в процессе присутствует периодическая составляющая;
3) параметры центрированной по текущей среднедекадной температуре воздуха нормированной корреляционной функции процесса изменения среднедекадной температуры воздуха в период с 3 декады апреля по 2 декаду сентября:
а) время спада корреляции ![]() декады;
декады;
б) средний полупериод колебаний ![]() декады,
декады,
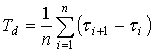 ,
,
где ![]() - абсциссы последовательных экстремумов корреляционной функции;
- абсциссы последовательных экстремумов корреляционной функции;
n - число пар экстремумов;
в) средняя круговая частота ![]() дек-1,
дек-1,
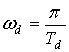 ;
;
г) среднее значение логарифмического декремента затухания корреляционной функции ![]() ,
,
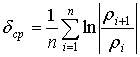 ,
,
где ![]() - ординаты последовательных экстремумов корреляционной функции.
- ординаты последовательных экстремумов корреляционной функции.
Анализ статистических показателей процесса изменения температуры воздуха позволил достичь вывода о том, что нормально распределенными можно считать месячные и декадные величины. Месячные величины не удовлетворяют условию заблаговременного учета, а использование среднесуточных величин температуры воздуха требует значительного объема обрабатываемой информации.
В итоге предпочтительными для проектирования ситуационного использования сельскохозяйственной техники мы считаем среднедекадные значения температуры воздуха. Использование декадных значений удобно и с точки зрения использования метеорологических прогнозов при проектировании.
Дифференцированный учет коэффициентов погодности позволяет адаптировать производственные процессы в растениеводстве к складывающимся погодным условиям при оптимизации их технико-технологических параметров.
Результаты исследований представлены в открытой печати, в том числе в монографиях, рекомендованных Учебно-методическим объединением вузов по агроинженерному образованию и Министерством сельского хозяйства Российской Федерации в качестве учебных пособий для студентов высших учебных заведений по агроинженерным специальностям [237 и др.].
Проведем сравнение (таблица 3.2) средневзвешенных значений предлагаемых коэффициентов погодности kn с коэффициентами использования времени по метеоусловиям КИМ [16], дифференцированных ВИМ по трем группам механизированных полевых работ:
- весенняя предпосевная обработка почвы, посев и основная обработка почвы;
- междурядная обработка;
- уборка зерновых и сена.
На основании таблицы 3.2 необходимо установить, возможно ли расхождение значений kn и КИМ отнести за счет случайных отклонений или это расхождение существенно и, следовательно, точность применяемых методик по определению коэффициентов погодности нами и ВИМ является значимо различной.
Таблица 3.2 - Коэффициенты kn и КИМ , дифференцированные по видам работ
|
Месяц |
Декада |
Весенняя предпосевная обработка почвы, посев |
Междурядная обработка |
Уборка зерновых и сена |
|||
|
kn |
КИМ |
kn |
КИМ |
kn |
КИМ |
||
|
04 |
3 |
0,54 |
0,83 |
- |
|||
|
05 |
1 2 3 |
0,63 0,76 0,75 |
0,85 0,86 0,85 |
0,88 0,87 0,88 |
0,98 0,99 0,98 |
- - 0,69 |
- - 0,75 |
|
06 |
1 2 3 |
0,79 - - |
0,82 - - |
0,87 0,86 0,85 |
0,95 0,89 0,68 |
0,66 0,70 0,68 |
0,70 0,64 0,53 |
|
07 |
1 2 3 |
- |
0,81 0,87 0,85 |
0,88 0,91 0,91 |
0,66 0,71 0,71 |
0,62 0,66 0,66 |
|
|
08 |
1 2 3 |
- 0,82 0,83 |
- 0,84 0,81 |
0,86 - - |
0,95 - - |
0,71 0,69 0,75 |
0,70 0,72 0,66 |
|
09 |
1 2 3 |
0,74 0,74 0,59 |
0,75 0,72 0,72 |
- |
0,65 0,69 0,56 |
0,60 0,60 0,60 |
|
|
10 |
1 |
0,35 |
0,63 |
|
0,35 |
0,54 |
|
Для этой цели используем методику парного сравнения, которая является более тонким аппаратом проверки, чем обычное сравнение двух средних [238].
Таким образом, проверке подлежит гипотеза ![]() , альтернативной к ней является гипотеза
, альтернативной к ней является гипотеза ![]() . Критерием для проверки может служить статистика
. Критерием для проверки может служить статистика
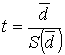 ,
,
где 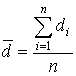 - средняя разность между наблюдениями;
- средняя разность между наблюдениями;
![]() - разность между наблюдениями в i паре;
- разность между наблюдениями в i паре;
n - число пар наблюдений;
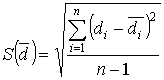 - среднее квадратическое отклонение разностей между наблюдениями.
- среднее квадратическое отклонение разностей между наблюдениями.
При нормальном распределении разностей ![]() t-статистика имеет распределение Стьюдента с числом степеней свободы
t-статистика имеет распределение Стьюдента с числом степеней свободы ![]() .
.
Результаты расчетов сведены в таблицу 3.3.
Таблица 3.3 - Результаты сравнения kn и КИМ
|
Виды работ |
|
t |
t0,05 |
|
Весенняя предпосевная обработка почвы, посев и основная обработка почвы |
10 |
0,91 |
2,23 |
|
Междурядная обработка |
9 |
0,61 |
2,23 |
|
Уборка зерновых и сена |
13 |
0,19 |
2,16 |
Из таблицы 3.3 следует, что результаты проверки гипотезы ![]() с помощью t-критерия при уровне значимости
с помощью t-критерия при уровне значимости ![]() позволяют утверждать, что полученные данные не расходятся со значениями, вычисленными ВИМ.
позволяют утверждать, что полученные данные не расходятся со значениями, вычисленными ВИМ.
