Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Методы повышения эффективности механизированных производственных процессов по условиям их функционирования в растениеводстве: Учебное пособие

Арютов Б. А., Важенин А. Н., Пасин А. В.,

3.6. Оценки в потребности и обеспеченности производственных процессов техникой при различных условиях их функционирования

Предпримем попытку прогноза и оценки экстремальных условий функционирования производственных процессов в растениеводстве, когда потребное количество технических средств превышает нормативное для типичных хозяйств Нижегородской области.

При прогнозировании состояния сложной системы возможно применение более агрегированных, более простых моделей, которые могут дать приемлемые прогнозы состояния сложной системы. Принимая во внимание это положение, рассмотрим грубую агрегированную модель динамики изменения потребности типичного хозяйства в тракторах на протяжении ряда лет. Эта модель представляет собой простую однородную цепь Маркова с двумя состояниями.

Будем считать, что условная вероятность пребывания системы в состоянии S_j в момент t зависит только от состояния системы в момент t-1:

.   (3.48)

Такой дискретный случайный процесс называется дискретной цепью Маркова [255]. Если вероятности перехода во времени не изменяются (  для всех t), то цепь называется однородной. Эволюция системы, описываемая однородной цепью Маркова, будет полностью задана, если известны начальное состояние (начальное распределение вероятностей) системы и матрица переходных вероятностей .

Рассмотрим закодированные последовательности наступления лет с экстремальными условиями эксплуатации тракторов Т-150К, ДТ-75М и МТЗ-80 соответственно:

              (3.49)

где символом «1» обозначен год, когда потребность в тракторах превышает нормативное значение, а символом «0» - год, когда потребность в тракторах меньше или соответствует нормативу. Таким образом будем считать, что потребность в тракторах каждый год может соответствовать одному из двух состояний, обозначаемых «1» или «0», и с наступлением очередного года переходит в новое состояние или остается в прежнем.

Проверим статистическую гипотезу о том, что последовательность {x_m} представляет собой поcледовательность независимых событий (нулевая гипотеза), а не простую цепь Маркова (альтернативная гипотеза). Для этого необходимо подсчитать значение выражения

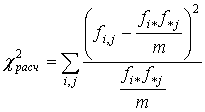,                                (3.50)

где   - частота переходов из состояния S_i в состояние S_j за один шаг (год);

т + 1 - объем выборочной последовательности состояний из цепи Маркова.

.                              (3.51)

Очевидно

.

Известно, что предельным распределением для выражения (3.50) будет  с (r - 1)² степенями свободы. В рассматриваемом случae имеется всего два состояния, т. е. r = 2.

Проведя расчеты по формуле (3.50), получаем  для последовательностей изменения потребного количества тракторов Т-150К, ДТ-75М, МТЗ-80 соответственно: 4,17; 4,57; 5,77. Табличное значение величины  с одной степенью свободы ((r - 1) = 1) при 5-процентном уровне значимости  и при 2,5-процентном уровне значимости .

Таким образом, гипотеза о том, что межгодовая динамика наступления лет с экстремальными условиями эксплуатации сельскохозяйственной техники идентична поведению простой цепи Маркова с двумя состояниями, не противоречат имеющимся наблюдениям.

Оценки максимального правдоподобия переходных вероятностей

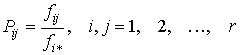,                          (3.52)

состоятельны и асимптотически не смещенные. Поэтому в результате расчета матрицы переходных вероятностей для последовательностей изменения потребного количества тракторов Т-150К, ДТ-75М, МТЗ-80 соответственно имеют вид:

;

;

.

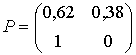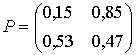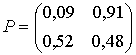Правомерно утверждать следующее. Для тракторов Т-150К состояние «1» является неопределенным в том смысле, что переход из него в состояние «0» или же снова в состояние «1» за один шаг примерно равновероятно, хотя имеет место тенденция к состоянию «1» (Р₁₁ = 0,62). Для тракторов ДТ-75М, МТЗ-80 не определено состояние «0». Однако для тракторов Т-150К, если нынешнее состояние «0», то следующим наверняка будет состояние «1» (P₂₁ = l). Потребность в тракторах ДТ-75М из состояния «1» перейдет за один шаг в состояние «0» с вероятностью 0,85. Потребность в тракторах МТЗ-80 из состояния «1» перейдет за один шаг в состояние «0» с вероятностью 0,91.

Таким образом, существующий уровень стохастичности в поведении системы изменения ежегодной потребности в тракторах хозяйств центральной части Нижегородской области делает задачу надежного краткосрочного прогнозирования далеко не тривиальной. Естественно, ее решение не под силу рассмотренной выше марковской модели.