Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Методы повышения эффективности механизированных производственных процессов по условиям их функционирования в растениеводстве: Учебное пособие

Арютов Б. А., Важенин А. Н., Пасин А. В.,

4.2.4. Методика обработки экспериментальных данных

При изучении производственных процессов в растениеводстве, в ходе которых участвуют и взаимодействуют многие эксплуатационные факторы при изменяющихся условиях, задача оптимизации становится многофакторной, экстремальной. Решать ее приходится при неполном знании механизма рассматриваемых явлений, не поддающихся описанию аналитическими методами.

Решаемые задачи можно объединить в два основных вида:

- выявление количественных зависимостей между эксплуатационными характеристиками производственного процесса (в нашем случае составляющие баланса времени смены);

- отыскание оптимальных значений эксплуатационных характеристик производственного процесса (под оптимальностью понимается получение наилучших результатов в конкретных условиях его функционирования).

Задачи первого вида приводят к интерполяционному эксперименту. Для решения задач второго вида может использоваться экстремальный эксперимент.

Основой для формализации объекта исследования служит модель «черного ящика». Идея заключается в том, что производственный процесс представляется как некоторая локализованная система, механизм функционирования которой неизвестен. Известно, однако, что объект может пребывать в различных состояниях. Об этом можно судить, измеряя некоторые его параметры. Их называют откликами.

Наблюдая за откликами можно судить об изменении состояния объекта исследования. Изменение состояния объекта происходит под воздействием внешних причин (условий функционирования). Их можно локализовать в виде отдельных воздействий, называемых факторами. Факторы - это переменные воздействия на производственный процесс, влиянию которых приписывается его переход из одного состояния в другое.

В зависимости от того, возможно ли воздействовать на факторы, эксперимент обычно классифицируют на активный, пассивный и активно-пассивный [263, 264 и др.]. При активном эксперименте все факторы полностью доступны для установки нужного уровня фактора. При активно-пассивном эксперименте доступны для управления лишь некоторые факторы, остальные можно только измерять. Наконец, при пассивном эксперименте можно только измерять значения факторов, но нельзя на них воздействовать. Мы имеем дело с активно-пассивным экспериментом. О планировании эксперимента в этом случае можно говорить лишь в смысле использования математического аппарата теории планирования эксперимента для обработки результатов наблюдений.

Если факторы действительно ответственны за изменение состояния объекта, то представляет интерес установление соответствия между наборами значений факторов и состояниями объекта. Некоторое значение фактора называется его уровнем. Соотношение между множествами уровней факторов и значениями отклика называется функцией отклика:

.

Геометрический образ функции отклика называется поверхностью отклика в факторном пространстве.

Экспериментом называется вся совокупность опытов, обеспечивающая получение оптимального значения целевой функции (в случае экстремального эксперимента), либо уравнения поверхности отклика (в случае интерполяционного эксперимента) с приемлемой степенью точности.

Опытом называется часть эксперимента, соответствующая некоторой фиксированной комбинации уровней факторов, для которой опытным путем определяется значение функции отклика.

Планом эксперимента называется таблица, в которой перечислены значения всех факторов в каждом из опытов. Каждый столбец этой таблицы представляет отдельный фактор, каждая строка - отдельный опыт.

В описательном эксперименте используется полнофакторный план эксперимента. Это такой план, при котором используются все возможные сочетания уровней факторов, но ни одно из этих сочетаний не повторяется. Если число уровней для всех факторов одинаково (наиболее распространенный случай), то необходимое число опытов определяется выражением

,

где N  - число опытов;

m- число уровней по каждому фактору;

k - число факторов.

Число уровней варьирования факторов при полнофакторном плане выбирается в результате компромисса между желанием получить как можно меньшую ошибку (это требует увеличения числа уровней) и стремлением сократить затраты ресурсов на проведение эксперимента, что побуждает сокращать число уровней.

Алгоритм формирования плана полнофакторного эксперимента представляется следующим образом.

1. В первой строке плана эксперимента для всех факторов записываем нижний уровень.

2. При заполнении каждой следующей строки для всех факторов, кроме последнего, повторяем предыдущие значения. Для последнего фактора в текущей строке ставим следующий (в порядке возрастания) уровень.

3. Повторяем шаг 2 до тех пор, пока не будет записан верхний уровень последнего фактора.

4. В следующей строке повторяем предыдущие значения для первых k-2 факторов. Для фактора k-1 записываем следующий по порядку его уровень. Для фактора k записываем нижний уровень.

5. Повторяем шаги 3 и 4 до тех пор, пока для факторов k-1 и k будет записан верхний уровень.

6. Для фактора k-2 записываем следующий по порядку его уровень, а для всех последующих факторов - нижний уровень. Уровни остальных факторов не меняем.

7. Повторяем эти действия до тех пор, пока все факторы окажутся на верхнем уровне. Это будет последняя строка плана эксперимента.

Описанный алгоритм формирования плана эксперимента - один из возможных. Можно начинать не с нижних уровней факторов, а с верхних. Можно также перебирать факторы, начиная не с последнего, а с первого. Возможны и другие модификации алгоритма. Важно лишь обеспечить выполнение двух условий:

1) ни одна из комбинаций уровней факторов не должна повторяться;

2) в план должны быть включены все возможные комбинации уровней.

Полнофакторный эксперимент позволяет уменьшить число опытов, что особенно важно при дорогостоящих экспериментах. Однако в функции отклика закладываются математические ожидания показателей характеристик исследуемого процесса. Но процессы могут быть совершенно не сравнимы при одинаковых статистических характеристиках. Равенство математических ожиданий еще не говорит об идентичности процессов. Не безразличность внутренней структуры процессов изменения их параметров отрицательно сказывается на результатах эксперимента. По этой причине полнофакторный эксперимент проводился на стадии подготовки к организации самофотографии рабочего времени с целью выявления элементов рабочего процесса, подлежащих исследованию.

Для функции отклика наиболее часто используются полиномы.

Определение значений коэффициентов полинома можно выполнить несколькими методами. Наиболее распространенным является метод наименьших квадратов, хотя в отдельных случаях могут быть метод наименьших модулей, минимаксный метод и др. При любом методе аппроксимация сводится к решению системы линейных уравнений. При этом совокупность выходных значений рассматривают как выборку реализации случайной величины без учета возможных взаимных связей между ними. Для такой модели процесса вычисляют числовые характеристики случайной величины (среднее значение и характеристики отклонений от среднего значения).

Таким образом, в такой вероятностной модели ограничиваются рассмотрением случайного процесса как простой совокупности реализации случайной величины, т.е. процесс упрощается и изучается как бы в статике при каких-то фиксированных условиях опыта.

Сельскохозяйственные агрегаты - сложные динамические системы, работают в условиях изменяющихся внешних воздействий, обусловленных многочисленными и разнообразными факторами.

Функционирование сельскохозяйственного агрегата как динамической системы удобно рассматривать как реакцию на входные внешние возмущения и управляющие воздействия. Поэтому наиболее общей схемой любого агрегата независимо от его назначения является схема по принципу вход-выход. В такой схеме анализ процесса осуществляется по динамике прохождения и преобразования переменных. В качестве входных принимаются все внешние возмущения (условия функционирования) и управляющие воздействия (со стороны водителя и инженерной службы), а выходных - совокупность параметров, которые определяют эффективность производственных процессов.

Такой подход к построению модели функционирования сельскохозяйственного агрегата и определяет его представление в виде динамической системы, осуществляющей преобразование входных воздействий в выходные.

Динамическая система является более сложной, но и более содержательной будет модель процесса в виде случайной функции неслучайного аргумента (в нашем случае времени t), значения которой при любом  будут случайными величинами. При этом аргумент в общем случае может принимать разные значения из множества . Таким образом, в данной модели случайный процесс представляется в виде множества случайных величин. При обработке такой модели процесса получают более содержательную информацию и не только в виде обычных числовых характеристик, определяющих взаимные связи между ординатами, но и его спектр частот.

Среди методов, характеризующих свойства временного ряда, особое место отводится вычислению коэффициентов автокорреляции ( ). Последние представляют собой коэффициенты корреляции, измеряющие взаимосвязь исходного ряда и этого же ряда, но сдвинутого на  шагов во времени (с лагом равным ). Последовательность коэффициентов автокорреляции ,  = 1, 2, ..., п, дает достаточно глубокое представление о внутренней структуре изучаемого процесса.

Для начала найдем коэффициент автокорреляции при условии, что  = 1, ряд сдвинут на один шаг во времени. Таким образом получим два ряда переменных:  и , т.е. для расчета коэффициента корреляции имеются следующие пары наблюдений: , всего n-1 пар.

.

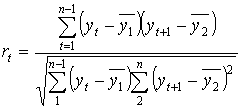Здесь 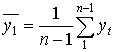 - средний уровень первого ряда;  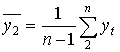- средний уровень второго ряда.

Воспользовавшись выражениями для определения суммы квадратов отклонений и ковариаций, получим следующую рабочую формулу:

.

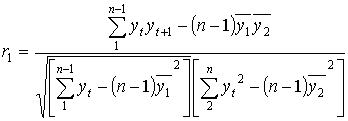Для запаздывания на  шагов во времени имеем

,

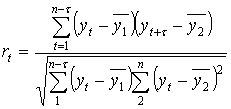где

; .

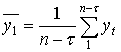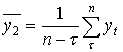Рабочую формулу можно записать следующим образом:

.

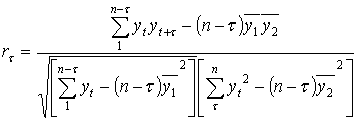Применяя коэффициент корреляции в качестве меры связи, нужно иметь в виду, что он получен на основе данных выборки и, следовательно, подвержен влиянию случайности. Если объем выборки небольшой, то найти выборочную ошибку этой величины достаточно сложно, поэтому вместо практикуемого обычно определения ошибки коэффициента корреляции целесообразно проверить гипотезу о его значимости (существенности), т.е. существенно ли  отличается от нуля или это отличие можно приписать влиянию случайности, связанной с выборкой. Проверка значимости осуществляется путем сопоставления табличного [265 и др.] и расчетного значений t - статистики. Последняя определяется по формуле

.

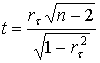Величина t здесь следует t - распределению Стьюдента. Найденное по данной формуле значение сопоставляют с табличным значением при n - 2 степенях свободы.

Как следует из формулы, значение t полностью определяется числом наблюдений и величиной коэффициента корреляции. Поэтому нетрудно для заданного числа степеней свободы найти наименьшее значение коэффициента корреляции, при котором нулевая гипотеза может быть отклонена с заданной вероятностью. Таблица таких значений приведена в [266].

При расчете  следует помнить, что с увеличением  число пар наблюдений соответственно уменьшается. При небольшом числе наблюдений значимыми оказываются лишь высокие значения коэффициента корреляции (например, при n=12 и уровне значимости 0,05 только r >0,576 оказываются значимыми). Отсюда следует, что наибольшее значение  должно быть таким, чтобы число пар наблюдений оказалось достаточным для вычисления . В практике ориентируются на правило, согласно которому  [238]. Некоторые исследователи [79 и др.] рекомендуют число наблюдений не менее 300, т.к. при этом вопрос значимости коэффициентов корреляции отпадает.

При большой протяженности исследуемого ряда расчет  можно упростить. Для этого находят отклонения не от средних коррелируемых рядов, а от общей средней всего ряда.

В этом случае

,

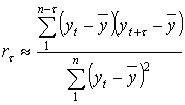где .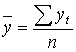

График, на котором показаны значения  для каждой данной величины , называется коррелограммой. Анализ коррелограмм оказывается весьма полезным при вскрытии закономерностей развития временных рядов.

Эти характеристики являются моментными функциями распределения случайного процесса и определяют его структуру во временной области.

Такое представление данных эксперимента дает содержательную информацию, необходимую при объективной оценке эксплуатационных условий функционирования производственных процессов в растениеводстве.