Научная электронная библиотека

Методы повышения эффективности механизированных производственных процессов по условиям их функционирования в растениеводстве: Учебное пособие

Арютов Б. А., Важенин А. Н., Пасин А. В.,

5.3. Алгоритм структурной оптимизации производственных процессов и его реализация в условиях растениеводства

Цель эксперимента - найти лучшую модель, которую можно было бы реализовать практически.

В существенно сложных задачах, подобных рассматриваемой, для определения паретовского множества во всем исследуемом пространстве необходимо проведение очень большого числа экспериментов на компьютере. Поиск оптимального решения целесообразно вести в два этапа: глобальный (грубый) обзор пространства параметров и локальное исследование окрестностей параметров моделей, попавших в таблицу испытаний. В подобных ситуациях определение начальных (улучшаемых) моделей составляет важнейшую задачу. В этой связи, а также в условиях отсутствия информации о связности допустимого множества решений, что характерно для задач оптимального проектирования, принципиальным фактором является равномерный тщательный обзор пространства параметров и построение таблицы испытаний. Все без исключения модели в таблице испытаний могут быть использованы в качестве начальных (улучшаемых) для локального исследования.

В области изменения заданных параметров (5.3) при определенных функциональных ограничениях (5.4) - (5.7) было поведено 1500 испытаний по отбору моделей. В таблицу испытаний (табл. 5.1) попало 113 моделей; функциональный коэффициент эффективности отбора .

Таблица 5.1 - Результаты испытаний 1


1	2	3	4	5	6	7	8
042	0,125	002	9,71	002	0,77	083	376
043	0,125	045	9,71	004	0,77	084	386
044	0,125	071	9,71	045	0,77	110	386
048	0,125	097	9,71	048	0,77	086	404
049	0,125	006	10,32	071	0,77	112	404
050	0,125	046	10,32	074	0,77	087	415
054	0,125	072	10,32	097	0,77	113	415
055	0,125	098	10,32	100	0,77	077	468
056	0,125	004	11,01	006	0,79	103	468
060	0,125	048	11,01	008	0,79	078	479
061	0,125	074	11,01	046	0,79	104	479
062	0,125	100	11,01	049	0,79	037	498
064	0,125	010	11,17	072	0,79	080	498
039	0,131	014	11,17	075	0,79	089	498
040	0,131	018	11,17	098	0,79	097	498
041	0,131	047	11,17	101	0,79	106	498
045	0,131	073	11,17	057	0,83	002	506
046	0,131	099	11,17	060	0,83	081	507
047	0,131	008	11,62	083	0,83	107	507
051	0,131	049	11,62	086	0,83	006	516
052	0,131	075	11,62	112	0,83	038	526
053	0,131	101	11,62	058	0,85	090	526
057	0,131	001	11,71	061	0,85	098	526
058	0,131	039	11,71	084	0,85	100	532
059	0,131	065	11,71	087	0,85	091	544
063	0,131	091	11,71	110	0,85	079	551
031	0,139	005	12,32	113	0,85	101	551
032	0,139	040	12,32	001	0,86	105	551
065	0,143	066	12,32	003	0,86	004	562
066	0,143	092	12,32	039	0,86	008	565
067	0,143	021	12,41	042	0,86	092	565
068	0,143	051	12,41	065	0,86	094	572
069	0,143	077	12,41	068	0,86	082	579
070	0,143	103	12,41	091	0,86	108	579
071	0,143	012	12,47	094	0,86	001	586
072	0,143	016	12,47	005	0,88	018	589
073	0,143	020	12,47	007	0,88	095	594
074	0,143	050	12,47	040	0,88	005	597
075	0,143	076	12,47	043	0,88	003	643
076	0,143	102	12,47	066	0,88	007	651

Продолжение таблицы 5.1

1	2	3	4	5	6	7	8
097	0,154	057	12,94	069	0,88	020	651
098	0,154	083	12,94	092	0,88	071	651
099	0,154	003	13,01	095	0,88	017	669
100	0,154	023	13,01	021	1,03	072	673
101	0,154	042	13,01	022	1,03	085	687
102	0,154	052	13,01	051	1,03	111	687
009	0,159	068	13,01	054	1,03	074	708
010	0,159	078	13,01	077	1,03	088	716
011	0,159	094	13,01	080	1,03	114	716
012	0,159	104	13,01	103	1,03	019	726
029	0,159	009	13,17	106	1,03	065	732
030	0,159	013	13,17	024	1,04	075	732
001	0,172	017	13,17	055	1,04	066	753
002	0,172	041	13,17	081	1,04	068	788
003	0,172	067	13,17	107	1,04	045	815
004	0,172	093	13,17	023	1,05	069	815
021	0,172	031	13,51	052	1,05	014	817
022	0,172	033	13,51	078	1,05	025	826
005	0,182	035	13,51	104	1,05	048	843
006	0,182	037	13,51	031	1,24	026	847
007	0,182	063	13,51	032	1,24	046	847
008	0,182	089	13,51	033	1,24	016	874
023	0,182	007	13,62	034	1,24	049	875
024	0,182	043	13,62	035	1,24	057	888
033	0,185	058	13,62	036	1,24	013	898
034	0,185	069	13,62	037	1,24	039	898
013	0,238	084	13,62	038	1,24	058	909
014	0,238	095	13,62	063	1,24	042	924
015	0,238	110	13,62	064	1,24	060	924
016	0,238	022	13,71	089	1,24	040	927
027	0,238	054	13,71	090	1,24	061	937
028	0,238	080	13,71	012	1,37	015	954
091	0,244	106	13,71	016	1,37	035	954
092	0,244	025	13,87	020	1,37	043	956
093	0,244	027	13,87	050	1,37	036	977
094	0,244	029	13,87	076	1,37	010	1046
095	0,244	053	13,87	102	1,37	012	1102
096	0,244	079	13,87	010	1,38	009	1126
035	0,278	105	13,87	014	1,38	099	1127
036	0,278	060	14,24	018	1,38	102	1155
083	0,357	086	14,24	047	1,38	093	1167
084	0,357	112	14,24	073	1,38	011	1183
085	0,357	024	14,32	099	1,38	096	1195
086	0,357	055	14,32	062	1,43	073	1274
087	0,357	081	14,32	088	1,43	021	1294
088	0,357	107	14,32	114	1,43	023	1304

Продолжение таблицы 5.1

1	2	3	4	5	6	7	8
110	0,357	059	14,32	059	1,44	022	1322
111	0,357	085	14,32	085	1,44	024	1333
112	0,357	111	14,32	111	1,44	027	1333
113	0,357	011	14,47	011	1,46	076	1333
114	0,357	015	14,47	015	1,46	067	1355
017	0,476	019	14,47	019	1,46	028	1358
018	0,476	044	14,47	044	1,46	033	1400
019	0,476	070	14,47	070	1,46	070	1411
020	0,476	096	14,47	096	1,46	034	1428
025	0,476	032	14,81	009	1,47	059	1511
026	0,476	034	14,81	013	1,47	062	1539
037	0,556	036	14,81	017	1,47	051	1715
038	0,556	038	14,81	041	1,47	052	1736
077	0,556	061	14,81	067	1,47	054	1743
078	0,556	064	14,81	093	1,47	055	1764
079	0,556	087	14,81	026	1,63	031	1851
080	0,556	090	14,81	028	1,63	030	1862
081	0,556	113	14,81	030	1,63	032	1880
082	0,556	026	15,17	056	1,63	047	1978
089	0,556	028	15,17	082	1,63	050	2006
090	0,556	030	15,17	108	1,63	041	2058
103	0,556	056	15,17	025	1,64	044	2087
104	0,556	082	15,17	027	1,64	063	2302
105	0,556	108	15,17	029	1,64	064	2331
106	0,556	062	15,70	053	1,64	053	2566
107	0,556	088	15,70	079	1,64	056	2595
108	0,556	114	15,70	105	1,64	029	2830

Среди отобранных 113 моделей наиболее производительной оказалась модель : Т-150К + МВУ-8 → 2(Т-150 + СП-11 + 2КПС-4 + 8БЗСС-1,0) → 2(МТЗ-82 + СП-11 + 2ВИП-5,6 + 2∙3ККШ-6) → 3(Т-150 + СП-11 + 3СЗА-3,6), работающая по схеме б (рисунок 5.4). Наиболее экономична по трудовым затратам и расходу топлива модель : 2(МТЗ-82 + МВУ-5) → 2(Т-150 + КШУ-12) → МТЗ-82 + СП-11 + 2ВИП-5,6 + 2∙3ККШ-6 → Т-150 + СП-11 + 3СЗА-3,6, работающая по схеме а (рисунок 5.4). Самая дешевая по критерию модель : МТЗ-82 + МВУ-5 → Т-150 + РВК-5,4 → Т-150 + СП-11 + 3СЗА-3,6, соответствующая схеме в (рисунок 5.4).

Из таблицы испытаний 1 видно, что улучшить модели , , по всем локальным критериям нельзя, что является следствием достаточно высокого качества исследуемых машин.

Принимая в качестве начальной модель, параметры которой соответствуют центру многогранника допустимого множества решений, можно сделать следующий вывод. Улучшить ее одновременно по всем локальным критериям не представляется возможным, т.к. критериальные ограничения этой модели соответствуют пустому допустимому множеству решений.

Поэтому ослабим критериальное ограничение по 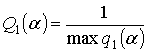до 0,15 (новая постановка задачи). После отбора данных в таблицу испытаний (таблица 5.2) попало 13 моделей; (ранее был 0,08). При этом ; ; ; .

Таблица 5.2 - Результаты испытаний 2


097	0,154	002	9,71	002	0,77	083	376
098	0,154	097	9,71	004	0,77	097	498
100	0,154	006	10,32	097	0,77	002	506
101	0,154	098	10,32	100	0,77	006	516
001	0,172	004	11,01	006	0,79	098	526
002	0,172	100	11,01	008	0,79	100	532
004	0,172	008	11,62	098	0,79	091	544
005	0,182	101	11,62	101	0,79	101	551
006	0,182	001	11,71	083	0,83	004	562
008	0,182	091	11,71	001	0,86	008	565
091	0,244	005	12,32	091	0,86	094	572
094	0,244	083	12,94	094	0,86	001	586
083	0,357	094	13,01	005	0,88	005	597

В таблицу испытаний 2 не вошли модели, работающие о схеме б (рисунок 5.4), т.е. схема построения технологического процесса по условию не эффективна.

В таблице испытаний 3 (таблица 5.3) приведены паретовские модели, определенные с учетом следующих критериальных ограничений: ; ; и .

Таблица 5.3 - Результаты испытаний 3


097	0,154	002	9,71	002	0,77	083	375
002	0,172	097	9,71	097	0,77	097	498
083	0,357	083	12,94	083	0,83	002	506

Заслуживает внимания модель : МТЗ-82 + МВУ-5 → Т-150 + КШУ-12 → МТЗ-82 + СП-11 + 2ВИП-5,6 + 2∙3ККШ-6 → 2(Т-150 + СП-11 + 3СЗА-3,6), соответствующая схеме г (рисунок 5.4). Из паретовских модель равноценна модели по и , но уступает ей по 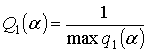и . Поэтому модель следует отнести к бесперспективным.

Не эффективной оказалась и работа по схеме а (рисунок 5.4). Из множества моделей, работающих по этой схеме, в паретовское вошла только бесперспективная модель .

Модель превосходит модель по , и , но уступает ей по . Поэтому на данном этапе (стадии эскизного проектирования) модели и можно признать равноценными.

Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»

(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)

«Современные проблемы науки и образования» список ВАК ИФ РИНЦ = 1,006

«Фундаментальные исследования» список ВАК ИФ РИНЦ = 1,674

«Современные наукоемкие технологии» список ВАК ИФ РИНЦ = 0,940

«Успехи современного естествознания» список ВАК ИФ РИНЦ = 0,775

«Международный журнал прикладных и фундаментальных исследований» ИФ РИНЦ = 0,593

«Международный журнал экспериментального образования» ИФ РИНЦ = 0,425

«Научное Обозрение. Биологические Науки» ИФ РИНЦ = 0,400

«Научное Обозрение. Медицинские Науки» ИФ РИНЦ = 0,801

«Научное Обозрение. Экономические Науки» ИФ РИНЦ = 0,871

«Научное Обозрение. Педагогические Науки» ИФ РИНЦ = 0,733

«Научное Обозрение. Технические Науки» ИФ РИНЦ = 0,695

«European journal of natural history» ИФ РИНЦ = 0,301

«Международный студенческий научный вестник»

Издание научной и учебно-методической литературы ISBN РИНЦ DOI

РЕЦЕНЗИИ и ОТЗЫВЫ
кандидатов и докторов наук
на статьи, авторефераты, диссертации, монографии, учебники, учебные пособия

Академия Естествознания готовит к изданию реестр новых научных направлений, разработанных российскими учеными

Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

5.3. Алгоритм структурной оптимизации производственных процессов и его реализация в условиях растениеводства

Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания