Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Методы повышения эффективности механизированных производственных процессов по условиям их функционирования в растениеводстве: Учебное пособие

Арютов Б. А., Важенин А. Н., Пасин А. В.,

6.1. Допустимое расписание полевых механизированных работ

Качество функционирования современного производства во многом определяется решениями, принимаемыми на этапах календарного планирования и оперативного управления. Наряду с улучшением качества плановых решений все более жесткими становятся требования к сокращению сроков их выработки, повышению оперативности и гибкости управления [270].

Многие практические ситуации приводят к необходимости изучения многостадийных обслуживающих систем, т.е. таких систем, в которых процесс обслуживания каждого требования состоит из нескольких последовательных стадий, на каждой из которых это требование обслуживается тем или иным прибором или совокупностью приборов. Так, посев зерновых включает несколько последовательных операций, каждая из которых выполняется некоторым МТА (погрузка семян, погрузка минеральных удобрений, транспортировка семян и минеральных удобрений, непосредственно посев).

В наиболее общей формулировке задачи составления расписаний состоят в следующем. С помощью некоторого множества ресурсов должна быть выполнена некоторая фиксированная система заданий. Цель заключается в том, чтобы при заданных свойствах заданий и ресурсов, и наложенных на них ограничениях найти эффективный алгоритм упорядочения заданий, оптимизирующий или стремящийся оптимизировать желаемую меру эффективности. В качестве основных мер эффективности рассматриваются, как правило, длина расписания и среднее время пребывания заданий в системе [271]. Модели этих задач являются детерминированными то есть вся информация, на основе которой принимаются решения об упорядочении, известна заранее. Задания и все данные о них предполагаются известными в начальный момент времени t=0.

Модель процесса упорядочения представляется в виде совокупности моделей, описывающих ресурсы, систему заданий, ограничения предшествования и меры оценки расписаний. В большинстве моделей технические ресурсы состоят из набора процессоров . В зависимости от особенностей задачи, они являются либо идентичными, либо одинаковыми только по функциональным возможностям, но разными по быстродействию, либо разными как по возможностям, так и по быстродействию [245, 272].

В общей модели мы можем предусмотреть набор дополнительных ресурсов , некоторое (возможно, пустое) подмножество которых используется на протяжении всего выполнения задания с некоторым процессором. Общее количество ресурса типа N задается положительным числом, μ резервный ресурс - числом δ.

Общая система заданий (работ) для заданного набора ресурсов может быть определена как система

,                                         (6.1)

где   - набор работ для выполнения;

 - ограничения на последовательность выполнения работ.

 - матрица размера , элемент которой - время выполнения работ.

Полагаем, что , если i не может быть выполнено и для каждого n существует, по крайней мере, одна i, для которой . В случае, когда все МТА идентичны,  обозначает время выполнения любым МТА.

 - набор, r-я компонента которого представляет собой количество резервного (дополнительного) ресурса, необходимого для выполнения i работ, .

 - веса, интерпретируются как комплексные затраты на выполнение работы в технологической системе, которые в общем случае могут быть произвольными функциями параметров, связанных с I_t. Считаем S_i постоянными величинами для однотипных условий функционирования. Таким образом, «стоимость» завершения задания I_t в момент t равна просто S_i · t.

Ограничения при составлении расписаний в общем виде могут быть [273]:

1. Составление расписаний без прерываний - работа раз начавшись, не может быть прервана, т. е. выполнение работы всегда доходит до конца.
2. Составление расписаний с прерываниями - разрешается прерывать работу выполняемую МТА; при этом полагаем, что общее время, требуемое для выполнения работы, остается неизменным и при прерываниях отсутствуют потери времени обслуживания.
3. Составление расписаний с помощью списка - предполагается, что вначале готовится упорядоченный список работ (список приоритетов). Последовательность, в соответствии с которой работы назначаются на МТА, составляется путем многократного просмотра списка. В частности, если появляется освободившийся МТА, то список начинает просматриваться сначала и просматривается до тех пор, пока не найдется первая невыполненная работа i, которая готова к выполнению. Работа считается готовой к выполнению на данном МТА, если выполнение всех предшественников i завершено и имеющегося количества ресурсов N достаточно для того, чтобы обеспечить её завершение в допустимые сроки. Это задание назначается для выполнения на свободный МТА. Мы предполагаем, что каждый просмотр осуществляется мгновенно. Кроме того, если одновременно два или более МТА оказываются свободными, мы предполагаем, что сначала назначается работа на N₁ затем на N₂ затем на N₃ и так далее. Для удобства записи предполагаем, что список упорядочивается слева направо и записывается в виде .

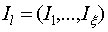При этом прерывания не рассматриваются формально, расписание может быть определено как некоторое отображение, которое, в общем случае, сопоставляет каждой работе последовательно из одного или более непересекающихся временных интервалов, лежащих в  с выполнением следующих требований:

а). На каждый интервал назначается один МТА;

б). Сумма длин интервалов равна времени выполнения работы, с учетом разной скорости их выполнения;

в). Никакие два интервала, относящиеся к разным работам, назначенным на один и тот же МТА, не перекрываются;

г). Учтены ограничения на порядок выполнения работ и использование дополнительных видов ресурсов;

д). На отрезке  не существует интервалов, на которых ни один из МТА не был бы наделен какой^: либо работой (т.е. в расписании не разрешается иметь МТА свободными, если остаются незавершенными работы).

В расписаниях без прерываний для каждой работы отводится ровно один интервал, а при составлении расписаний с помощью списка еще накладывается требование, чтобы ни один МТА не мог быть свободным, если имеются готовые к выполнению работы, которые могут быть на него назначены [274].

В основном рассматривают четыре основных показателя эффективности [273], длину расписания или максимальное время завершения

                                      (6.2)

среднее взвешенное время завершения или прохождения

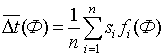.                                    (6.3)

Основная проблема заключается в нахождении эффективных алгоритмов, позволяющих находить среди всех расписаний такие, для которых эти величины достигают минимума (максимума) [161].

Расширим общую модель, сопоставив каждой работе i_t положительное число , которое назовем директивным сроком для этого работы. Директивный срок представляет собой момент времени, к которому желательно завершить выполнение работы. Определим временное смещение работы i_t в расписании Ф как разность  и запаздывание - как . Такие критерии эффективности, как минимальные и средние значения временного смещения запаздывания, в нашем случае представляют большой интерес. Как и в случае со временем ожидания, легко видеть, что расписание, минимизирующее среднее взвешенное время выполнения, минимизирует и среднее взвешенное временное смещение; для среднего взвешенного запаздывания это не так.

Существуют задачи, в которых директивные сроки не должны нарушаться (т.е. ). Одной из таких задач является задача о нахождении минимального числа МТА, необходимых для выполнения системы работ к общему крайнему сроку . Данная задача связана с задачей об упаковке в контейнеры. Имеется близкая связь между подходами к построению переборных или приближенных методов с помощью динамического программирования и с помощью метода ветвей и границ [161].

Особое внимание мы обратили на один из способов приближенного решения задач теории расписаний, сущность которого заключается в следующем. Сначала решается задача нахождения допустимого расписания для технологических средств, как основных так и резервных. Результатом решения этой задачи являются интервалы директивного времени, в которые выполняются отдельные работы без потерь урожая. Эти интервалы являются основанием для последующего точного распределения МТА по работам, с учетом их соответствия сезонным условиям и ресурсосбережения. Решение задачи завершается построением сезонного расписания, в соответствие с выбранным экономическим критерием, учитывающим как основные так и резервные технико-технологические средства [275].

Декомпозицию исходной задачи на две более простые мы закладываем в основу метода упорядочения параллельных производственных процессов растениеводства, функционирующих в различных погодных условиях. Первая задача решается на основании учета климатических, погодных и агробиологических особенностей процессов в сроках использования технических средств - составления допустимого расписания. Допустимые расписания параллельных производственных процессов составляются с учетом потребностей каждой работы к условиям её проведения. Допустимые расписания образуют форму, которая должна уточняться содержанием - ресурсными, организационными и экономическими возможностями производства. В этом отношении они имеют самостоятельное значение при любом разнообразии технической оснащенности и обеспеченности другими ресурсами.

Уменьшение информации о разнообразии погодных ситуаций допустимыми расписаниями на пять сезонов-аналогов, с заблаговременным выбором конкретного из них, придает определенность в выборе методов повышения эффективности производственных процессов растениеводства.

Решение задачи составления допустимого расписания осуществляется на основании разработанных нами в предыдущей главе оценок условий сезонов-аналогов и оптимальных значений некоторых параметров производственных процессов растениеводства. Алгоритм задачи допустимого расписания реализован в программах разработанных на языках программирования Бейсик-5А [146], Паскаль [276].

Структура первой программы «Сезонные допустимые расписания использования технологических систем в производственных процессах растениеводства» состоит из 3 модулей со следующими возможностями:

1. Расчет допустимого расписания и темпов выполнения работ для пяти сезонов-аналогов.
2. Выбор по текущему коэффициенту подобия одного из пяти сезонов-аналогов. Расчет для него допустимого расписания и темпов выполнения работ в заданный период времени.
3. Расчет допустимого расписаниями и темпов выполнения работ в предстоящий период времени с учетом сложившихся условий сезона.

Программа для ЭВМ «Сезонные технико-технологические резервы производственных процессов растениеводства» позволяет определить необходимые допустимые технологические резервы для выполнения i-ой работы в агротехнический срок в -сезон-аналог и составить календарный план.