
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
6.3.2. Экономико-математическая модель сезонного резервирования и использования технолого-технических средств в растениеводстве
Процесс разработки и реализации экономико-математической модели состоит из нескольких этапов: постановка задачи, построение модели, обоснование метода её решения, подготовка исходной информации, решение задачи на ЭВМ и анализ полученных результатов. В разработанной нами методике применяется несколько линейных моделей. Выходные параметры первой модели являются входными параметрами для второй модели, а выходные параметры второй модели будут входными для третей модели и так далее.
Отличие каждой модели от классической состоит, прежде всего, в допустимых сроках и темпах выполнения полевых механизированных работ (см. методику расчета, пункт 6.1) и возможности заблаговременного принятия решения.
Как правило, задачу нахождения оптимального состава МТП решают формированием годового объема механизированных работ, используя внедренные и перспективные технологические карты на возделывание и уборку сельскохозяйственных культур с разбивкой его на расчетные периоды.
Экономико-математическая модель оптимизации состава и использования технолого-технических средств производственного процесса растениеводства, с учетом привлечения машин и исполнителей из МТС и других структур, определяется целевой функцией получения максимальной прибыли
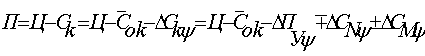 , (6.28)
, (6.28)
где Ц - планируемая стоимость растениеводческой продукции (выращенного урожая), руб.;
![]() - комплексные затраты, связанные с использованием существующих и привлекаемых в агропредприятие технолого-технических средств и исполнителей (механизаторов), руб.;
- комплексные затраты, связанные с использованием существующих и привлекаемых в агропредприятие технолого-технических средств и исполнителей (механизаторов), руб.;
![]() - комплексные затраты при использовании существующих в агропредприятии техники и механизаторов, руб.;
- комплексные затраты при использовании существующих в агропредприятии техники и механизаторов, руб.;
![]() - приращение комплексных затрат в ψ-ый сезон-аналог, руб.;
- приращение комплексных затрат в ψ-ый сезон-аналог, руб.;
![]() - приращение потерь урожая в ψ-ый сезон-аналог, руб.;
- приращение потерь урожая в ψ-ый сезон-аналог, руб.;
![]() (-) - затраты, связянные с привлечением резервной техники или ее покупкой, руб.;
(-) - затраты, связянные с привлечением резервной техники или ее покупкой, руб.;
![]() (-) - затраты, связанные с привлечением резервных исполнителей, руб.;
(-) - затраты, связанные с привлечением резервных исполнителей, руб.;
![]() (+) - доход, получаемый за счет использования собственной резервной техники вне агропредприятия, руб.;
(+) - доход, получаемый за счет использования собственной резервной техники вне агропредприятия, руб.;
![]() (+) - доход, получаемый за счет использования резервных исполнителей (механизаторов) вне агропредприятия, руб.
(+) - доход, получаемый за счет использования резервных исполнителей (механизаторов) вне агропредприятия, руб.
С помощью этого критерия разработаны условия: исключения, замены отдельной операции, очередности выполнения работ, сочетания способов. Как следует из формулы, прибыль определяется разностью между планируемой стоимостью растениеводческой продукции и комплексными затратами на выполнение годового объема работ МТП при ее производстве. При уменьшении комплексных затрат прибыль возрастает на искомую величину
![]() (6.29)
(6.29)
При решении задачи необходимо выполнять следующие ограничения.
1) неотрицательность переменных
![]() ; (6.30)
; (6.30)
![]() .
.
2) ограничение площади культуры l, возделываемой по технологии g, соответствующей ψ сезону и ![]() сорту в подразделении k
сорту в подразделении k
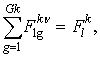
![]() . (6.31)
. (6.31)
3) все планируемые работы в необходимых объемах должны быть выполнены в установленные агротехнические сроки по выбранным вариантам технологий g, всеми технологически допустимыми φ-агрегатами по допустимым темпам работ, соответствующим складывающимся условиям сезонов-аналогов
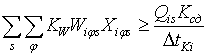 . (6.32)
. (6.32)
4) взаимосвязанные работы должны выполняться в определенной последовательности при согласованности способов их выполнения:
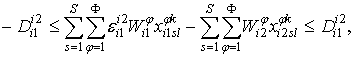
![]() , (6.33)
, (6.33)
а) одновременно не может быть использовано машин больше имеющегося в наличии в предприятии и резерва техники из МТС и других уровней:
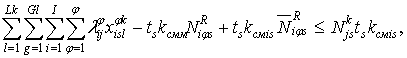
![]() , (6.34)
, (6.34)
6) количество механизаторов в каждый период не должно быть больше имеющегося в предприятии и резервного из МТС, РТК и других уровней:
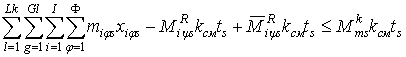 , (6.35)
, (6.35)
где ![]() - индексы соответственно работы, агрегата, цикла, машины, культуры по возделываемой технологии, подразделения, обслуживающего агрегат, исполнителя;
- индексы соответственно работы, агрегата, цикла, машины, культуры по возделываемой технологии, подразделения, обслуживающего агрегат, исполнителя;
![]() - удельные эксплуатационные затраты (без реновации), руб./га;
- удельные эксплуатационные затраты (без реновации), руб./га;
![]() - производительность, га/сут.;
- производительность, га/сут.;
![]() - количество агрегатов, шт.;
- количество агрегатов, шт.;
KW - коэффициент использования производительности агрегата;
aj - коэффициент отчислений на реновацию по машине;
E - коэффициент эффективности капитальных вложений;
Бj - балансовая стоимость машины, руб.;
Xj - количество машин, шт.;
CM - оценка затрат на одного механизатора, необходимых при выполнении годового объема работ в агропредприятии, руб./чел.;
XM - количество механизаторов, обслуживающих МТП в течение года, в том числе вновь принятых в штат агропредприятия, чел.;
![]() - количество машин в агрегате, шт.;
- количество машин в агрегате, шт.;
![]() - количество исполнителей, обслуживающих агрегат, шт.;
- количество исполнителей, обслуживающих агрегат, шт.;
![]() - количество резервных механизаторов привлекаемых в агропредприятие из МТС и других уровней, чел.;
- количество резервных механизаторов привлекаемых в агропредприятие из МТС и других уровней, чел.;
![]() - количество резервных механизаторов целесообразно используемых вне агропредприятия, чел.;
- количество резервных механизаторов целесообразно используемых вне агропредприятия, чел.;
![]() - количество резервных МТА, привлекаемых в агропредприятие из МТС и других уровней, шт.;
- количество резервных МТА, привлекаемых в агропредприятие из МТС и других уровней, шт.;
![]() - количество резервных МТА, целесообразно используемых вне агропредприятия, шт.;
- количество резервных МТА, целесообразно используемых вне агропредприятия, шт.;
![]() - площадь возделываемой культуры по технологии, соответствующей сезону и сорту, га;
- площадь возделываемой культуры по технологии, соответствующей сезону и сорту, га;
![]() - возможное смещение в объемах взаимосвязанных работ, га, т.;
- возможное смещение в объемах взаимосвязанных работ, га, т.;
![]() - коэффициент соизмеримости объемов работ (применяется, когда взаимосвязанные работы имеют различные единицы измерения);
- коэффициент соизмеримости объемов работ (применяется, когда взаимосвязанные работы имеют различные единицы измерения);
![]() - количество имеющихся машин в агропредприятии, шт.;
- количество имеющихся машин в агропредприятии, шт.;
![]() - количество имеющихся в штате агропредприятия механизаторов, чел.;
- количество имеющихся в штате агропредприятия механизаторов, чел.;
ts - продолжительность периода, дни.
Оптимальная продолжительность выполнения отдельных работ ППР определяется из целевой функции. Запишем целевую функцию на min комплексных затрат следующим образом:
![]() . (6.36)
. (6.36)
Тогда
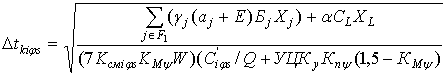 . (6.37)
. (6.37)
где ![]() - доля данной работы в годовом объеме;
- доля данной работы в годовом объеме;
![]() - доля рабочего времени на данной работе в общем времени работы механизатора в течение года.
- доля рабочего времени на данной работе в общем времени работы механизатора в течение года.
Из-за большого объема решаемой задачи (множество работ, агрегатов), как правило, количество периодов ограничивают (за счет корректировок сроков работ). В связи с этим решение задачи становится не совсем адекватно реальным условиям производства. К тому же расчет состава и структуры МТП по пиковым периодам пусть и достаточно прост и применяется многими авторами, но без комплексного подхода, без учета всех периодов-порой допускает значительные отклонения от истинного значения.
Базовая линейная модель (рис. 6.2), а их пять по каждому сезону-аналогу, решает задачу выполнения планируемых работ в необходимых объемах в установленные агротехнические сроки по допустимому расписанию без предварительной разбивки на периоды. В результате решения мы получаем не количество агрегатов, необходимых для выполнения всего объема работ, а количество заданий, которых больше, чем агрегатов - это результат перекрытия сроков. Поэтому нами используются методы, с помощью которых разрешается данная ситуация. Это и бинарные матрицы, основанные на булевой алгебре, и логические функции электронной таблицы Microsoft Excel и т.п.
С помощью вспомогательных матриц результаты базовой модели уточняются и автоматически поступают в первую модель (см. рис. 6.2). По каждой работе, по минимуму комплексных затрат в пределах допустимого расписания-определяются оптимальные сроки и количество агрегатов (трактористов). Потери урожая отсутствуют. Автоматически выводятся графики загрузки тракторов помарочно и в целом - суммарно. Анализ графиков создает возможность выявить пиковость и провалы в использовании тракторов. Разные временные интервалы загрузки тракторов позволяют провести упорядочение работы тракторов по методу составления расписания с помощью списка (пункт 6.1), для этого необходимо иметь набор нормативных технико-экономических показателей конкурирующих агрегатов. Снижение количества техники достигается за счет упорядочения работ, в некоторых случаях вынужденного исключения отдельных операций, (не значительно или менее влияющих на факт получения продукции, чем основные работы - формула 6.2), замены простых агрегатов на более производительные, в том числе комбинированные и комбайновые.
Во второй модели, кроме выше перечисленных действий, добавляется ограничение на трудовые ресурсы. Оптимизация состава и использования МТП ведется по минимуму комплексных затрат, но в отличие от первой модели в расчете функционируют оптимальные сроки выполнения работ и потери урожая свыше директивных сроков.
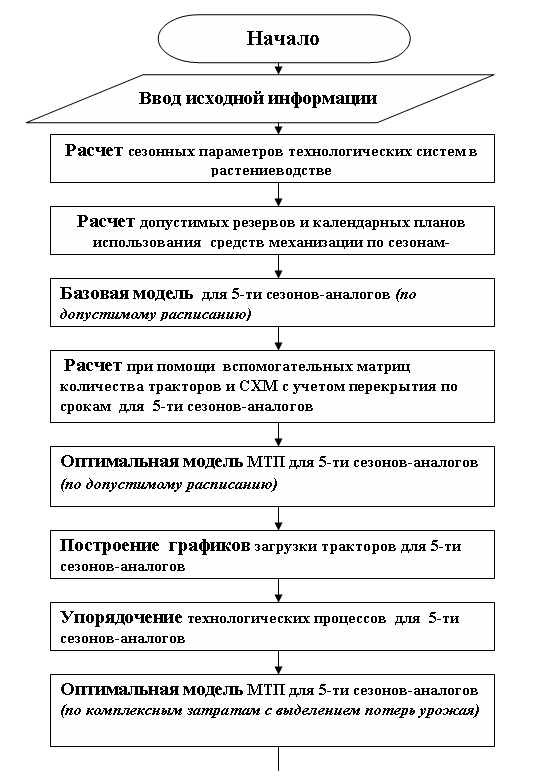
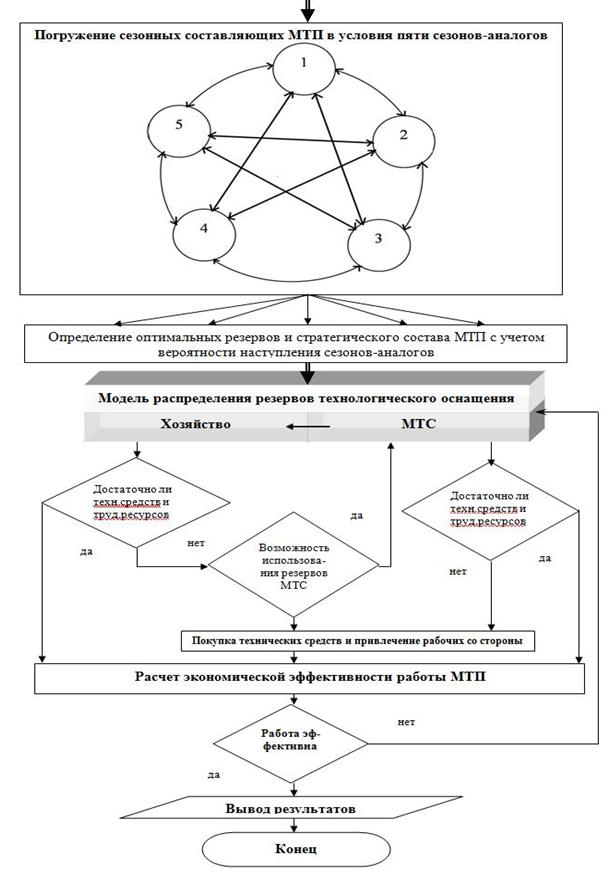
Рисунок 6.2 - Алгоритм автоматизированной системы проектирования стратегического состава МТП и сезонных резервов
технолого-технических средств
Рассчитанный для пяти сезонов-аналогов МТП является оптимальным для своих погодно-производственных условий. Это подтверждает и «погружение» сезонных составов МТП в условия пяти сезонов-аналогов. При погружении используются функции электронной таблицы Microsoft Excel, в частности, функция ПОИС ПОЗ. Комплексные затраты на проведение работ, соответствующим сезону МТП - минимальны по сравнению с другими исходами. Но оптимальное тактическое решение (сезонный состав техники) оптимально только относительно конкретно реализуемой ситуации - - сезона. Необходимо найти такое стратегическое решение (стратегический МТП), которое учитывало бы вероятности наступления всех сезонов - аналогов, которое являлось бы наилучшим для всех типов сезонов. В данной ситуации используется задача матричной игры, в которой стратегией является каждый сезон-аналог. Результатом матричной игры является определение оптимального стратегического МТП (по минимуму комплексных затрат). Для этого парка составляется третья модель (см.рис. 6.2), которая позволит определить необходимый состав МТП в предприятии и МТС, с учетом списания техники с баланса хозяйства, приобретения её и оказания услуг населению (в отдельные сезоны силами МТС).
