Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Частично пористые газостатические опоры шпиндельных узлов. Теория и эксперимент: монография

Космынин А. В., Виноградова С. В., Виноградов В. С., Щетинин В. С., Смирнов А. В.,

2.1. Уравнение Рейнольдса для определения давления газа в смазочном слое частично пористого подшипника

Для определения поля давления в зазоре частично пористого подшипника с внешним наддувом газа воспользуемся хорошо известной в теории газовой динамики системой уравнений:

• уравнения политропы ;
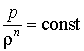• уравнения неразрывности ;
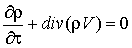• уравнения движения ;
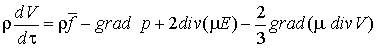• уравнения энергии .

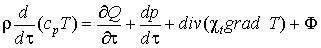В этих выражениях  - время, V - скорость газа,  - внешняя сила, отнесенная к единице массы газа, Е - тензор скоростей деформации,  - удельная теплоемкость при постоянном давлении, Q - внутренняя теплота,  - коэффициент теплопроводности, Ф - диссипативная функция, которая равна

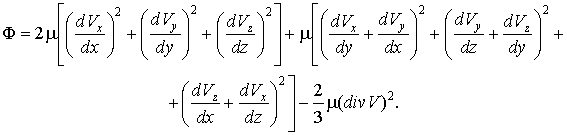
На основании работ [147, 148, 149] примем допущения относительно течения газа в пористой вставке и смазочном слое подшипника:

1. Течение газа в пористой среде считается вязким и ламинарным, подчиняющиеся закону Дарси, что позволяет считать коэффициент проницаемости пористого материала k_p постоянным.

2. Течение смазки в зазоре подшипника изотермическое, а сама смазка сжимаемая, удовлетворяющая уравнению состояния .

3. Толщина смазочного слоя такова, что позволяет пренебречь течением газа в направлении нормали к стенкам подшипника и считать давление в этом направлении неизменным.

4. Объемные и инерционные силы пренебрежительно малы по сравнению с силами вязкого трения и восстанавливающей силой смазочного слоя, уравновешивающей внешнюю нагрузку.

5. Течение газа в зазоре подшипника стационарное.

С учетом принятых допущений определим вид уравнения Рейнольдса для определения поля давления в зазоре подшипника с частично пористой стенкой вкладыша, изображенного на рис. 2.1.

 

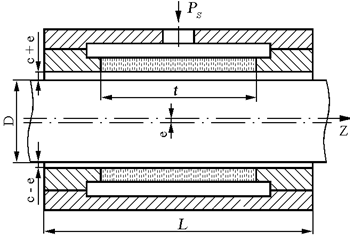
Рис. 2.1. Газостатический подшипник с пористыми вставками

Шпиндельный подшипник - однорядный, радиальный с равномерно расположенными по окружности пористыми вставками, выполненными в виде шпонок, количество которых в ряду наддува равно N_ВСТ.

Развернем цилиндрическую поверхность подшипника в плоскость и введем в рассмотрение декартовую систему координат (рис. 2.2).

 

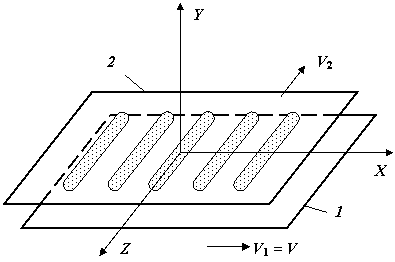
Рис. 2.2. Развертка поверхности газостатического подшипника:
1 - поверхность вала; 2 - поверхность вкладыша

Путем совместного решения уравнений неразрывности и расхода смазки в окружном направлении и через торец подшипника, с учетом четвертого допущения, выражение для определения поля давления в смазочном слое будет иметь вид:

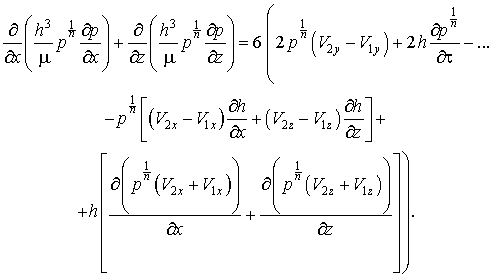
В области вкладыша подшипника, свободной от пористых вставок, имеем:

.

В области пористых вставок при тех же равенствах проекций скоростей только .

Таким образом, получим два дифференциальных уравнения, первое из которых соответствует области пористых вставок:

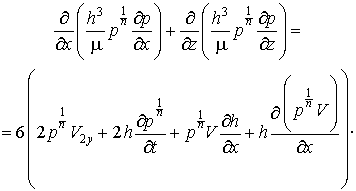                (2.1)

а второе - области, свободной от вставок:

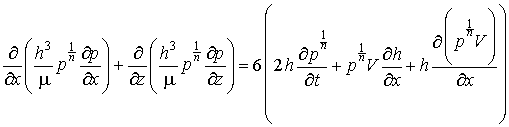. (2.2)

Объединяя выражения (2.1) и (2.2) в одно дифференциальное уравнение, получим:

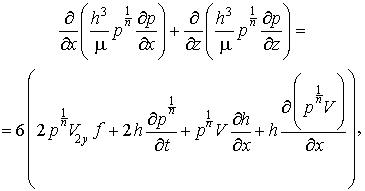                  (2.3)

где  - оператор (  в области вставок и  вне области вставок).

Считая процесс течения газа стационарным ( ) и изотермическим ( ), уравнение (2.3) приведем к виду:

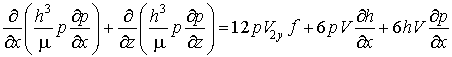.       (2.4)

После умножения левой и правой части уравнения (2.4) на 2 получим:

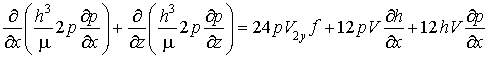.  (2.5)

Заметим, что:

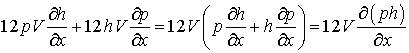             (2.6)

и

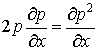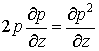,    .          (2.7)

С учетом выражений (2.6) и (2.7) дифференциальное уравнение (2.5) представим в виде:

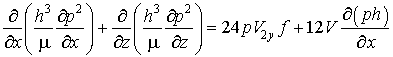.           (2.8)

В радиальных подшипниках с пористым вкладышем движение газа в области пористой матрицы происходит и в направлении нормали к поверхности. В работе [147] показано, что в соответствии с законом Дарси компонента скорости в этом направлении может быть определена по формуле:

.

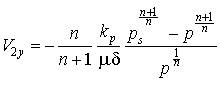Полагая процесс в пористой среде и смазочном слое изотермическим (n=1), найдем:

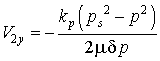.           (2.9)

Подставив уравнение (2.9) в (2.8), получим дифференциальное уравнение:

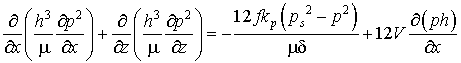.   (2.10)

Рассмотрим область интегрирования выражения (2.10) в переменных X и Z (рис. 2.3), имея в виду то, что в общем случае при симметричном расположении вставок относительно оси Х поле давления в зазоре подшипника также будет симметричным относительно этой оси.

 

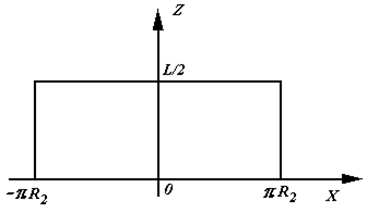
Рис. 2.3. Область интегрирования

Для показанной области интегрирования запишем дифференциальное уравнение распределения давления газа в зазоре подшипника в безразмерном виде.

С этой целью перейдем к относительным параметрам газа и координатам по формулам:

1. Относительная длина подшипника ;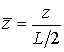

2. Относительное давление газа в зазоре подшипника ;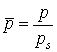

3. Относительный зазор между валом и вкладышем ;

4. Угловая координата .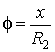

В безразмерных координатах область интегрирования задается неравенствами  и .

Подставив представленные выражения в уравнение (2.10), получим:

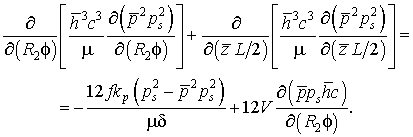
Преобразуем последнее уравнение к виду:

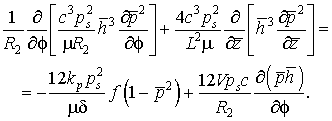                 (2.11)

Поскольку , то выражение (2.11) можно представить как

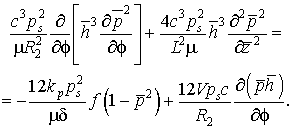                     (2.12)

После деления правой и левой части уравнения (2.12) на величину  получим:

.

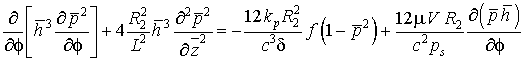Упростим последнее выражение. Для этого введем в него удлинение подшипника  и заметим, что поскольку средний радиальный зазор мал по сравнению с радиусами вала и вкладыша, то без большой ошибки окружную скорость вала запишем в виде .

Очевидно, что

.

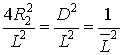Дополнительно введем переменные:

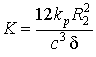 - параметр питания подшипника;

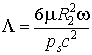 - число сжимаемости.

Таким образом, уравнение Рейнольдса для определения поля давления газа в смазочном слое подшипника с пористыми ограничителями расхода имеет вид:

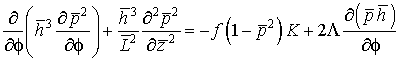,          (2.13)

где f = 1 в области пористых вставок и f = 0 в области свободной от вставок.