
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

Частично пористые газостатические опоры шпиндельных узлов. Теория и эксперимент: монография
Космынин А. В., Виноградова С. В., Виноградов В. С., Щетинин В. С., Смирнов А. В.,
2.3. Метод и алгоритм решения задачи
Решение дифференциального уравнения (2.16) с учетом граничных условий (2.17)-(2.27) выполняется итерационным методом Гаусса-Зейделя. Для этого вводится вспомогательный массив
При i = 1, 2, 3, ..., ![]() и j = 1, 2, 3, ...,
и j = 1, 2, 3, ..., ![]()
![]() . (2.37)
. (2.37)
Первые столбец и строка элементов массива V заполняются согласно равенствам:
![]() ; (2.38)
; (2.38)
![]() . (2.39)
. (2.39)
На основании выражения (2.6) значение каждого элемента массива V находится из решения уравнения:
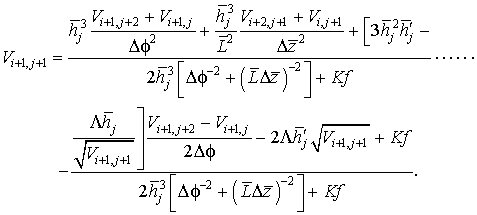 (2.40)
(2.40)
Как и выражение (2.16) данное уравнение не распространяется на элементы массива V, лежащих на границе пористых вставок. На этих границах, исходя из (2.28)-(2.34), используются формулы:
- на линии ![]() каждой k-й вставки
каждой k-й вставки
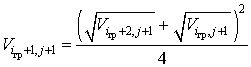 ,
, ![]() ; (2.41)
; (2.41)
- на линии ![]() каждой k-й вставки
каждой k-й вставки
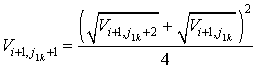 ,
, ![]() ; (2.42)
; (2.42)
- на линии ![]() каждой k-й вставки
каждой k-й вставки
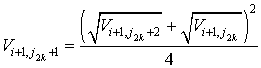 ,
, ![]() ; (2.43)
; (2.43)
- в точках с координатами (![]() )
)
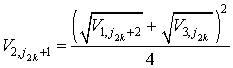 ; (2.44)
; (2.44)
- в точках с координатами (![]() )
)
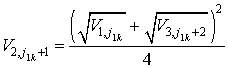 ; (2.45)
; (2.45)
- в точках с координатами (![]() )
)
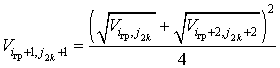 ; (2.46)
; (2.46)
- в точках с координатами (![]() )
)
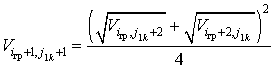 . (2.47)
. (2.47)
Для решения системы нелинейных уравнений методом Гаусса-Зейделя необходимо задать нулевое приближение искомой величины. В качестве таковой в данном случае выступают элементы массива ![]() . Их нулевое приближение задается согласно, представленным на рис. 2.6 графиком.
. Их нулевое приближение задается согласно, представленным на рис. 2.6 графиком.
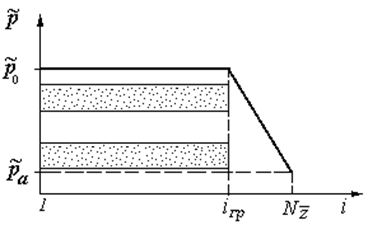
Рис. 2.6. Характер распределения относительного давления
в зазоре подшипника в нулевом приближении
Как видно из этого графика, в нулевом приближении элементы массива ![]() равны:
равны:
![]() ;
;
![]() ,
,
где ![]() - задаваемое значение относительного давления (
- задаваемое значение относительного давления (![]() ).
).
После заполнения массива ![]() значениями нулевого приближения
значениями нулевого приближения ![]() [по формулам (2.37)-(2.39)] расчет относительного давления в узлах конечноразностной сетки, выполняемый согласно выражениям (2.40)-(2.47), идет при
[по формулам (2.37)-(2.39)] расчет относительного давления в узлах конечноразностной сетки, выполняемый согласно выражениям (2.40)-(2.47), идет при ![]() и
и ![]() .
.
Это связано с тем, что, во-первых, в процессе итераций согласно граничному условию (2.18) происходит присваивание
![]() ,
,
а, во-вторых, в силу граничного условия (2.20)
![]() .
.
При этом заметим, что в ходе итераций, исходя из (2.38) и (2.39), поддерживаются равенства:
![]() ;
;
![]() .
.
Система уравнений (2.40)-(2.47) считается решенной при выполнении условия:
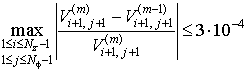 , (2.48)
, (2.48)
где m - число итераций.
Как показали вариантные расчеты подшипников при не вращающемся вале, столь высокое задание погрешности в (2.48) обеспечивает ошибку в определении угла ориентации нагрузки Ψ не выше одного градуса.
Выражение (2.48) является необходимым, но не достаточным условием завершения итерационного процесса. Последнее связано с тем, что в начальной стадии расчетов неизвестен угол ориентации нагрузки Ψ. Таким образом, при решении совокупной системы уравнений (2.40)-(2.47) неизвестными оказываются координаты ![]() и
и ![]() каждой вставки, что и является причиной второго итерационного цикла.
каждой вставки, что и является причиной второго итерационного цикла.
Для его проведения необходимо задать вполне определенную схему расположения вставок во вкладыше подшипника. Имея это в виду, в расчетах принято такое расположение вставок, когда центр одной из них находится на вертикальной оси симметрии вкладыша в нагруженной части подшипника.
Условие окончания второго итерационного цикла имеет вид:
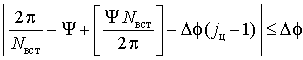 ,
,
где ![]() - номер горизонтальной линии, на которой находится ближайший к линии j = 1 центр какой-либо вставки.
- номер горизонтальной линии, на которой находится ближайший к линии j = 1 центр какой-либо вставки.
Описанные выше методика и алгоритм расчета легли в основу создания программы для ПВЭМ [151] по расчету эксплуатационных характеристик частично пористых однорядных газостатических опор шпиндельных узлов.