Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Методы построения активных фильтров подавления импульсных помех в сетях электропитания промысловых судов

Горева Т. С., Портнягин Н. Н.,

2.1.Кратномасштабный анализ, вейвлет преобразование

Кратномасштабные аппроксимации

Использование разрешения сигнала позволяет обрабатывать только нужные детали частных задач. В компьютерной визуализации Барт и Адельсон ввели кратномасштабную (мультиразрешающую) пирамиду, которая может быть использована первоначально для обработки изображения с низким разрешением, и затем выборочно повышает разрешение, если это необходимо.

Приближение функции f с разрешением 2^-j определяется дискретной решеткой отсчетов, которая обеспечивает локальные средние f в окрестностях, пропорциональных 2^j. Поэтому кратномасштабная аппроксимация состоит из набора решеток аппроксимации. Более формально приближение функции с разрешением 2^-j определяется как ортогональная проекция на пространство . Пространство V_j перегруппировывает всевозможные приближения с разрешением 2^-j . Ортогональная проекция f есть функция , которая минимизирует .

Кратномасштабные пространства

Последовательность замкнутых подпространств  из  образует кратномасштабную аппроксимацию, если удовлетворяется следующие шесть свойств:

 ;                        (2.1)

 ;            (2.2)

    ;                           (2.3)

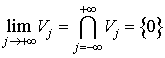;                             (2.4)

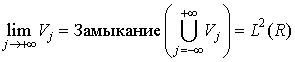.                   (2.5)

Существует функция θ такая, что семейство  есть базис Рисса V₀.

Дадим объяснения этим математическим свойствам. Свойство (2.1) означает, что V_j  инвариантно относительно сдвига, пропорционально масштабу 2^j. Это пространство может быть уподоблено равномерной решетке с шагом 2^j, которая характеризует приближение сигнала с разрешением 2^-j. Включение (2.2) - причинное свойство, согласно которому приближение с разрешением 2^-j содержит всю необходимую информацию для вычисления с более грубым разрешением 2^-j-1. Растяжение функции из V_j в 2 раза увеличивает в 2 раза подробности, и (2.3) гарантирует, что это определяет аппроксимацию с более грубым разрешением2^-j-1. Когда разрешение 2^-j стремиться к 0, то (2.4) означает, что мы теряем все детали f и

.                  (2.6)

С другой стороны, когда разрешение 2^-j стремиться к +∞, свойство (2.5) означает, что аппроксимация сигнала сходиться к первоначальному сигналу:

.               (2.7)

Когда разрешение 2^-j возрастает, скорость убывания погрешности аппроксимации  зависит от гладкости сигнала f.

Существование базиса Рисса  подпространства V₀ приводит к теореме дискретизации. Функция θ может быть интерпретирована как единичный элемент разрешения.

СуществуютА > 0 и В такие, что любая  может быть единственным образом разложена в ряд

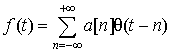,             (2.8)

где  

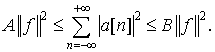         (2.9)

Эта энергетическая эквивалентность гарантирует, что разложения сигналов по 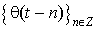 численно устойчивы. Используя свойства растяжения (1.3) и разложения (2.8), можно убедиться, что семейство  есть базис Рисса V_j с теми же границами Рисса A и B при всех масштабах 2^j.

Семейство  есть базис Рисса порождаемого им пространства V₀ тогда и только тогда, когда существуют A > 0 и B > 0 такие, что

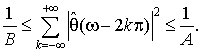                  (2.10)

Масштабирующая функция

Приближение f с разрешением 2^-j определяется как ортогональная проекция  на V_j. Чтобы вычислить эту проекцию, необходимо найти ортонормированный базис V_j. Следующая теорема ортогонализирует базис Рисса  и строит ортогональный базис каждого пространства V_j с помощью растяжения и сдвига единственной функции φ, называемой масштабирующей функцией.

Пусть  - кратномасштабная аппроксимация и φ - масштабирующая функция, преобразование Фурье которой есть

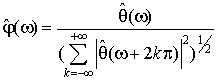.                      (2.11)

Обозначим

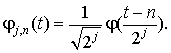
Семейство  есть ортонормированный базис V_j при всех .

Аппроксимация

Ортогональная проекция f на V_j получается при разложении по масштабирующему ортогональному базису

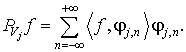               (2.12)

Скалярные произведения

               (2.13)

дают дискретную аппроксимацию с масштабом 2^j.

В виде свертки:

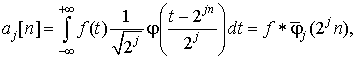                  (1.14)

где

Вейвлет-преобразования

Для анализа структуры сигнала самой разной длительности необходимы частотно-временные атомы с различными временными носителями. Вейвлет-преобразование раскладывает сигналы по растянутым и сдвинутым вейвлетам. Вейвлет - это функция  с нулевым средним значением:

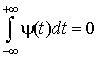.           (2.15)

Она нормирована, , и имеет центром t = 0. Семейство частотно-временных атомов получается в результате масштабирования  на величину s и сдвига на u:

.

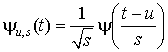Эти атомы остаются нормированными:  Вейвлет-преобразо­вание  от времени u и масштаба s есть

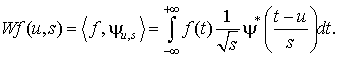
Линейная фильтрация

Вейвлет-преобразование может быть переписано в виде свертки

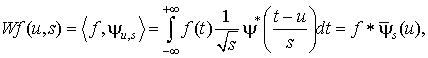       (2.16)

где .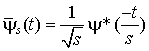

Преобразование Фурье  есть

.        (2.17)

Так как 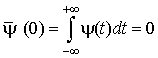, то ясно, что  - передаточная функция диапазонного фильтра. Свертка (2.16) вычисляет вейвлет-преобразование с растянутым диапазонным фильтром.