
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.5. Квадратное дерево вейвлет-пакетов
Базисы вейвлет-пакетов строятся в пространстве
![]() ,
,
имеющих одинаковые масштабы вдоль осей x1 и x2. Эти сепарабельные базисы вейвлет-пакетов связаны с квадратными деревьями и разбивают двумерную плоскость Фурье ![]() на квадратные области различных размеров. Сепарабельные базисы вейвлет-пакетов - это расширение сепарабельных вейвлет-базисов.
на квадратные области различных размеров. Сепарабельные базисы вейвлет-пакетов - это расширение сепарабельных вейвлет-базисов.
Если изображения приближаются с масштабом 2L, то с корнем квадратного дерева мы связываем пространство аппроксимации ![]() , объясняет,как разложить VL с помощью двоичного дерева вейвлет-пакетов пространств
, объясняет,как разложить VL с помощью двоичного дерева вейвлет-пакетов пространств ![]() , которые допускают ортогональный базис
, которые допускают ортогональный базис ![]() . Двумерное квадратное дерево вейвлет-пакетов состоит из сепарабельных пространств вейвлет-пакетов. Каждый узел этого квадратного дерева помечается масштабом 2j и двумя целыми числами:
. Двумерное квадратное дерево вейвлет-пакетов состоит из сепарабельных пространств вейвлет-пакетов. Каждый узел этого квадратного дерева помечается масштабом 2j и двумя целыми числами: ![]() и
и ![]() , и соответствует сепарабельному пространству
, и соответствует сепарабельному пространству
![]() . (2.32)
. (2.32)
В результате сепарабельный вейвлет-пакет при x = (x1, x2) есть
![]() .
.
Ортогональный базис ![]() получается как с6епарабельное произведение базисов вейвлет-пакетов
получается как с6епарабельное произведение базисов вейвлет-пакетов ![]() и
и ![]() и может быть записан как
и может быть записан как
![]() .
.
В корне ![]() вейвлет-пакет есть двумерная масштабирующая функция
вейвлет-пакет есть двумерная масштабирующая функция
![]() .
.
Одномерные пространства вейвлет-пакетов удовлетворяют равенствам
![]() и
и ![]() .
.
Из подстановки этих уравнений в (4.1.) следует, что ![]() есть прямая сумма четырех ортогональных подпространств
есть прямая сумма четырех ортогональных подпространств
![]() (2.33.)
(2.33.)
Эти подпространства расположены в четырех рожденных узлах квадратного дерева, как показано на рис.2.3. Допустимым квадратичным деревом называется любое квадратичное дерево, узлы которого имеют 0 или 4 рожденных.
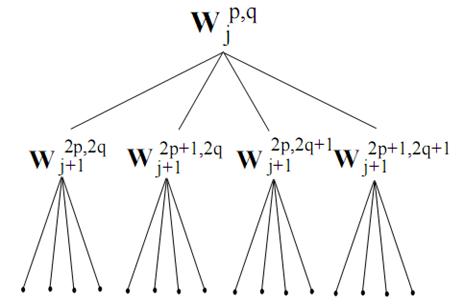
Рис. 2.3. Квадратичное дерево вейвлет-пакетов для изображений
строится рекурсивно разложением каждого сепарабельного
пространства на четыре подпространства
Пусть ![]() - индексы узлов у листьев допустимого квадратичного дерева. Рекурсивное применение сумм (1.33.) вдоль ветвей этого квадратичного дерева дает ортогональное разложение
- индексы узлов у листьев допустимого квадратичного дерева. Рекурсивное применение сумм (1.33.) вдоль ветвей этого квадратичного дерева дает ортогональное разложение ![]() :
:
![]() .
.
Поэтому объединение соответствующих базисов вейвлет-пакетов
![]()
есть ортонормированный базис ![]() .
.
Число базисов вейвлет-пакета
Число различных базисов в полном квадратном дереве вейвлет-пакетов глубины J равняется числу допустимых поддеревьев.
Число BJ базисов вейвлет-пакета в полном квадратичном дереве вейвлет-пакета в полном квадратном дереве вейвлет-пакетов глубины J удовлетворяет неравенствам
![]()
