Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Методы построения активных фильтров подавления импульсных помех в сетях электропитания промысловых судов

Горева Т. С., Портнягин Н. Н.,

2.2.4. Гладкость

Гладкость ψ оказывает в основном косметическое влияние на погрешность, вносимую пороговой обработкой и квантованием при вычислении вейвлет-коэффициентов. При восстановлении сигнала по его вейвлет-ко­эффициентам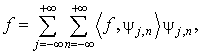  погрешность ε, добавляемая к коэффициенту , будет добавляться как вейвлет-коэффициент  восстанавливаемого сигнала. Если ψ - гладкий вейвлет, то и погрешность будет гладкой.

Измерение гладкости с помощью вейвлетов

Убывание амплитуды вейвлет-преобразования в зависимости от масштаба связано с равномерной и точечной гладкостью Липшица сигнала. Измерение этого асимптотического убывания эквивалентно приближению структур сигнала при масштабе, стремящемся к нулю. Пусть вейвлет  имеет n нулевых моментов и принадлежит Сⁿ с быстроубывающими производными. Это означает, что для любого  и  существует константа С_m такая, что

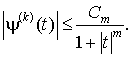             (2.25)

Если  удовлетворяет равномерному условию Липшица  на [a,b], то существуетА>0 такое, что

   .          (2.26)

Обратно, предположим, что f ограничена и что Wf(u,s) удовлетворяет (2.26) для нецелого α<n. Тогда f удовлетворяет равномерному условию Липшица α на  при любом

Неравенство (2.26) есть условие асимптотического убывания  при s, стремящемся к нулю. Прибольших масштабах это не накладывает никаких ограничений, так как неравенство Коши-Шварца гарантирует ограниченность вейвлет-преобразования:

При убывании масштаба Wf(u,s) измеряет мелкомасштабные изменения в окрестностях u. Так как  убывает как  на интервалах, где f удовлетворяет равномерному условию Липшица α.

Масштаб вейвлета s играет роль «локализованной» обратной частоты . Если [a,b] = R, то (2.26) есть необходимое и достаточное условие того, что f удовлетворяет равномерному условию Липшица α на R.

Если ψ имеет точно n нулевых моментов, то убывание вейвлет-пре­образования не дает информации о гладкости Липшица fпри . Если f удовлетворяет равномерному условию Липшица , то она принадлежит Сⁿи

где . Из этого следует, что ~ при малых масштабах, несмотря на более высокую гладкость f.

Если показатель Липшица α - целое число, то неравенство (2.26) недостаточно для того факта, что f удовлетворяет равномерному условию Липшица α.