Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

СРАВНИТЕЛЬНЫЙ АНАЛИЗ ИННОВАЦИОННОЙ АКТИВНОСТИ СУБЪЕКТОВ РОССИЙСКОЙ ФЕДЕРАЦИИ

Белоусова О. М.,

3.1. Методологический подход к оценке влияния выделенных экспертным путем факторов на результативность инновационной деятельности

Группировка показателей. Инновации измеряются многочисленными показателями. Численные значения десятков показателей представлены в открытом доступе на официальном сайте Росстата. Часть показателей естественно интерпретировать как входные показатели, а оставшиеся - как выходные. Входные показатели описывают материальные или человеческие ресурсы, связанные с изобретениями или разработками.

К ним относятся показатели инновационных возможностей (доля молодого населения, доля образованного населения, доступность средств массовой информации, включая интернет), показатели исследовательской работы (публичные и бизнес-проекты, доля высоких технологий и пр.), вложения в инновации (доля инновационных малых предприятий среди всех малых предприятий, инновационные расходы, вложения в информационные и коммуникационные технологии и др.).

Принципиальное отличие инноваций от изобретений заключается в том, что инновация позволяет создать дополнительную ценность. Следовательно, изобретение становится инновацией, когда произошло его успешное внедрение.

Поэтому выделяют выходные показатели инноваций, характеризующие возможности внедрения проведенных исследований, сделанных изобретений и отдачу вложенных средств.

К ним относятся показатели полезности выходных факторов (занятость в высокотехнологичном производстве, доля экспорта высокотехнологичной продукции, доля новых товаров в товарообороте и др.) и наличие интеллектуальной собственности (разного рода патенты и торговые марки).

Каждая группа факторов содержит, как сказано выше, целый ряд показателей. Использование индивидуальных показателей приводит к разному ранжированию регионов по инновационной привлекательности.

Поэтому при анализе применяют информацию по всем доступным показателям для увеличения надежности полученных результатов.

Оценка инновационной привлекательности регионов. Существуют различные способы параметрической оценки инновационного потенциала региона, связанной с использованием экзогенно заданным видом зависимости потенциала и входными показателями.

Стандартная методология (см. например, [21]) использует логистическую модель и Байесовский подход к принятию решений. Соответствующее моделирование состоит из двух этапов.

На первом этапе инновационность региона вычисляется как интенсивность инноваций, внедряемых фирмами, расположенными внутри этого региона. Предполагается, что у фирмы i в отрасли k есть выбор между двумя альтернативами: Z - придерживаться инновационной стратегии и  - не придерживаться инновационной стратегии.

Проводится оценка условной вероятности того, что отдельная фирма оказывается инновационной при заданном ее расположении в пространстве и известных структурных характеристиках. Эта вероятность обозначается как (см. формулу 3):

  (3)  где   принимает значения одной из двух альтернатив: Z или    обозначает вероятность, что фирма i в производственной отрасли k придерживается инновационной стратегии, S обозначает положение фирмы в пространстве, F₁,....., F_n - значения n структурных характеристик фирмы. Предполагается, что существует три возможных положения фирмы в пространстве

- S1 - положение фирмы в центральном регионе;

- S2 - положение фирмы в промежуточной зоне;

- S3 - положение фирмы на периферии.

Таким образом, веротяность   что фирма i в промышленной отрасли k развивает инновации, зависит от вероятности    нахождения фирмы в части Sj региона и вероятности P{F₁,...,.F_n} наличия разных наборов структурных характеристик, которые оцениваются заранее.

Стуктурные характеристики фирмы связаны с ее технологическими возможностями, известностью ее бренда, квалифицированностью рабочей силы и другими факторами. Условную вероятность вычисляют с помощью логистической модели (см. формулу 4):    (4) где коэффициенты , β₀, β₁ ,..., β_n подбираются с помощью обычной регрессии. Эта вероятность, таким образом, оценивает возможность выбора фирмой инновационной стратегии при наличии заданных структурных характеристик.

В уравнении логистической модели предполагается, что каждая из характеристик положительно коррелирует с инновациями - увеличение значения произвольного F_j увеличивает привлекательность для фирмы выбора инновационной стратегии.

На втором этапе оценивается инновационная привлекательность региона. Математически она записывается как условная вероятность заданного положения фирмы в пространстве и наличия заданных структурных характеристик при условии выбора инновационной стратегии (см. формулу 5):   (5)

По правилам вычисления условной вероятности, она находится как отношение вероятности одновременного выбора фирмой инновационной стратегии и наличия у этой фирмы заданных структурных характеристик и вероятности выбора фирмой инвестиционной стратегии в произвольных условиях, независимо от наличия структурных характеристик (см. формулу 6).    (6)

Преобразования числителя полученной дроби приводит к формуле для оцениваемой вероятности (см. формулу 7):    (7)

Входящие в полученную формулу вероятности оцениваются как соответствующие доли инновационных фирм по имеющимся статистическим данным. Таким образом, непосредственное применение логистической модели 2 позволяет оценить шансы, что фирма, расположенная в настоящее время в регионе, применяет инновационную стратегию, тогда как модифицированная модель 5 оценивает возможность региона притягивать инновационные фирмы в будущем [20].

Факторный анализ. Как было указано выше, включение большого количества показателей в анализ инновационной активности региона, с одной стороны, увеличивает надежность результата исследования, а с другой стороны, затрудняет получение и изложение результата, поскольку различные факторы могут действовать несогласованно по отношению к инновационной активности.

Следовательно, привлекая к анализу максимально полную информацию, необходимо сначала выделить статистическим способом малое количество показателей (на основе всех имеющихся данных), а затем проводить ранжирование регионов в соответствии с выделенными показателями.

Автоматическое сужение количества факторов проводится методом главных компонент [33, 36]. Формальная задача может быть поставлена как выделение заранее заданного количества показателей. Перед статистической обработкой данные должны быть унифицированы стандартным способом. Можно считать, что каждый показатель задаётся числом F_j, лежащим в интервале [0, F], где F - это наибольшее зафиксированное значение показателя (зависимость показателя от региона в обозначениях опущена). Все показатели нормируются наибольшим достижимым значением (см. формулу 8):   (8)

таким образом, что новые значения показателей (для которых сохраняются обозначения F_j) лежат в интервале [0, 1]. Итак, каждый регион i задается вектором показателей  

Требуется найти n-мерный вектор   и ортонормированный набор векторов    в n-мерном векторном пространстве, такие что сумма квадратов расстояний от векторов     до плоскости проходящей через указанные вектор будет наименьшей. Здесь m - это исходное количество показателей. Таким образом, требуется минимизировать сумму (см. формулу 9).    (9)  где k - требуемое количество остающихся показателей. Эта задача решается методами вариационного исчисления (рис. 7).

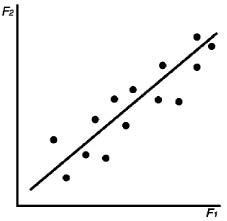
Рис. 7. Выделение главной компоненты для множества точек. Сумма квадратов отклонений от точек до прямой наименьшая среди всех прямых плоскости

Количество остающихся показателей можно также получить с помощью метода главных компонент. Для этого формулируется задача о поиске направлений, характеризующихся наибольшим рассеиванием. Эта задача решается последовательно.

Сначала находится направление, по которому рассеивание данных наибольшее. Затем исходные векторы проектируются на плоскость перпендикулярную этому направлению. При проектировании количество координат уменьшается на единицу.

Для проекций вновь формулируется задача - найти направление, по которому рассеивание данных наибольшее. Далее векторы снова проектируются вдоль только что найденного направления и опреация повторяется. На этом пути можно выделить все главные компоненты, а можно их выделять до тех пор, пока сумма квадратов расстояний до очередной выделенной компоненты не становится больше заданного числа (рис. 8).

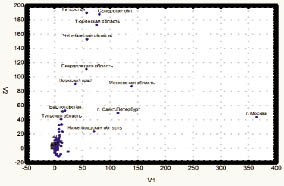 Рис. 8. Результаты анализа инновационного потенциала регионов РФ

Чтобы полностью автоматизировать алгоритм, вычисляются последовательные отклонения очередного выделенного направления от имеющихся данных. Как только впервые отклонения драматически выросли, процедура выделения главных компонент считатеся законченной.

Рассеивание данных определяется с помощью выборочной дисперсии. Пусть нормированный вектор   адаёт некоторое направление в n-мерном пространстве показателей. Тогда выборочная дисперсия данных вдоль заданного направления (см. формулу 10) - это:    (10)

Величина D минимизируется на первом шаге алгоритма. На втором шаге вычисляется ее аналог для проекции векторов вдоль найденного первого главного направления, и т.д.

Эмпирические правила прекращения процедуры выделения главных компонент связаны с ковариационной матрицей, приведенной в формуле 11:

  (11)

Простейшее правило айзера рекомендует выбирать компоненты до тех пор, пока   (12)

где _i - это собственные значения ковариационной матрицы V, расположенные в порядке убывания (см. формулу 12). Более тонкие правила рассчитаны на конкретные приложения [16].

Математически, выделенные направления являются линейной комбинацией исходных показателей. Поэтому предложить названия для выделенных направлений - непростая задача для экономиста. Одна из возможностей - интепретировать выделенные направления как агрегированные факторы, характеризующую группу показателей. В простейшем случае каждую группу факторов представляет один агрегированный показатель, найденный алгоритмически.

Пусть положение каждого региона задаётся одним входным и одним выходным показателями (рис. 9), каждый из которых в результате унифиации (деления на максимальное зафиксированное значения этого показателя) лежит на интервале [0, 1]. Очевидно, что среди двух регионов с одинаковым входным показателем инновации эффективнее в том регионе, где выходной показатель выше.

Аналогично, среди двух регионов с одинаковым выходным показателем, эффективнее тот, для которого входной показатель ниже. Другими словами, чем левее и выше расположени регион в соответствии с рис. 9, тем эффективнее в нем инновации. Эффективным фронтом называется множество точек, имеющих наибольший выходной показатель при наименьшем входном (верхние достижимые точки на графике).

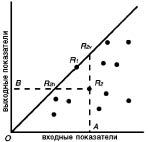
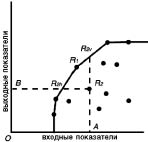
Рис. 9. Эффективный фронт (сплошная линия) инновационных показателей региона при постоянной (слева) и переменной (справа) отдачи от масштаба. (регионы обозначены точками)

Учитывая дискретность данных, эффектинвый фронт оценивается двумя способами. Пусть R_i - положение региона на графике (см. рис. 9, слева). Тогда эффективный фронт определяется как прямая OR_i, проходящая через начало координат, с наибольшим углом наклона. На рис. 9, слева, эта прямая обозначена OR₁. Это определение эффективного фронта предполагает постоянную отдачу от масштаба.

Однако существование постоянной отдачи от масштаба, по крайней мере, не очевидно. Поэтому [23] при достаточно большом количестве данных естественно определить эффективный фронт как набор отрезков, соединяющих самые левые и верхние точки (точное определение такое, что эффективный фронт является вогнутой кусочно-линейной границей, (см. рис. 7, справа).

Эффективность инноваций оценивается как в терминах входных, так и терминах выходных показателей [30]. Мера эффективности, ориентированная на входные показатели, измеряет возможное уменьшение входных показателей для достижения тех же самымх выходных показателей. Например, регион R₂ мог бы достигнуть того же выходного показателя при меньшем входном показателе. Соответствующая точка обозначена R_2h вместо R₂ на рис. 9. При постоянной отдаче от масштаба точка R_2h находится на прямой OR₁ (см. рис. 9), при переменной - на кусочно-линейной границе множества регионов. Отношение длин, приведенных в формуле 13:

  (13)

задаёт меру эффективности региона R₂. В соответствии с определением мера эффективности лежит между нулем и единицей как при постоянной, так и при переменной отдаче от масштаба.

Мера, ориентированная на выходные показатели измеряет насколько эти показатели улучшаемы при неизменном входном показателе. Для рассмотренного выше региона R соответствующая мера задается отношением длин (см. формулу 14):   (14)

как показано на рис. 9. В случае постоянной отдачи от масштаба меры μ_I и μ_O ориентированные на входные и выходные показатели, эквиваленты. В случае переменной отдачи от масштаба эти меры, вообще говоря, различны.

При анализе эффективности инновационной активности регионов необходимо принимать во внимание существование временных диапазонов, в течение которых сказывается влияние входных показателей на выходные.

При отсутствии ясной модели запаздывания, естественно использовать устойчивость эффективного фронта к синхронному изменению момента измерений входных и выходных данных в качестве меры корректности выбранной величины запаздывания. Другими словами, пусть
n - количество лет, прошедших между вычислением входного и выходного показателей.

Тогда для различных пар (t, t + n), соответствующим времени получения входного и выходного показателей, оценивается эффективный фронт. Затем вычисляется степень близости между различными фронтами. В качестве n выбирают такое число, что эффективные фронты оказываются наиболее близкими.

Предложенные методы не принимают во внимание различные виды неоднородности, типичные в задачах экономической географии [31] - неоднородность индивидуумов, фирм, регионов. С другой стороны указанная неоднородность влияет на используемые при эмпирическом анализе данные и, потому, неявно влияет на результаты анализа.

В рамках бурно развивающихся моделей новой экономической географии в литературе широко обсжудается вопрос о корректности учёта неявного влияния неоднородности на оценки инновационного потенциала и о взаимном влиянии инновационного потенциала, регионального развития, экономического роста и конкурентноспособности [15, 18, 48, 19, 34].

Неоднородность регионов. В основе объяснения неравенства регионов лежат идеи Хотеллинга. В модели Хотеллинга две фирмы продают идентичный продукт. Потребители равномерно распределены по линейному городу. При выборе продавца они принимают во внимание цену товара и расстояние, которое требуется преодолеть потребителю, чтобы совершить покупку.

Следовательно, неоднородность вводится на стадии моделирования: каждый потребитель характеризуется индивидуальными расстояниями до фирм. Фирмы конкурируют между собой, выбирая свое местоположение и назначая цену на товар. Если, принимая решение, потребитель больше ценит расстояние до ближайшей фирмы, чем цену товара, то фирмам следует располагаться в центре города. Напротив, если цена является основным фактором, влияющим на выбор потребителя, то ценовая конкуренция близко расположенных фирм проходит в соответствии с парадоксом Бертрана, вынуждая фирмы отклоняться от центра города.

Таким образом, введение пространственной неоднородности порождает как центростремительную, так и центробежную силы, объясняемые и интерпретируемые по-разному в различных приложениях.

Модель дуополии естественным образом распространяется на большее количество измерений. Одна координата соответствует расположению фирм в пространстве, остальные - потребительским характеристикам продукта. Irmen et. al. [25] показывают, что фирмы стремятся увеличить свои отличия вдоль наиболее важного для них направления и уменьшить вдоль остальных. Другими словами, фирмы минимизируют зону взаимных контактов.

Пока транспортные расходы относительно велики, фирмы располагаются далеко друг от друга. При значительном уменьшении транспортных расходов фирмы приближаются друг к другу в пространстве, выпуская всё новые и новые товары, тем самым, на смену пространственной удалённости фирм приходит разнообразие товаров [29].

Вывод [17] о том, что падение транспортных расходов, сравнимых с мерой разнообразия товаров, стимулирует фирмы к концентрации в месте наивысшего рыночного потенциала, находится в соответствии с подходом Кругмана [27], который объясняет появление агломераций при снижении транспортных расходов. В классической модели Рикардо международной торговли с постоянной отдачей от масштаба внутри страны производятся относительно дешёвые товары.

Снижение издержек на производство относительно дорогого товара освобождает ресурсы для производства дополнительного количества более конкурентного товара. Если наиболее конкурентные товары в странах - торговых партнёрах отличаются, то имеет место торговый оборот.

Следовательно, торговля между странами осуществляется за счёт постоянной отдачи от масштаба в производстве и неоднородности между странами, предполагаемой заданной экзогенно.

Предположив существование возрастающей отдачи от масштаба в соответствии с моделью Диксита-Стиглица монополистической конкуренции, Кругман [27, 28] построил модель международной торговли, в которой несимметричность равновесия достигается за счёт внутренней динамики.

Развивая теорию Кругмана, Ottaviano et. al. [32] построили близкую модель, допускающую аналитическое решение (в отличие от [27]) и позволяющую сделать качественные выводы о влиянии истории городов на их последующее развитие.

В работе [31] показано, что при достаточно малых или достаточно больших транспортных расходах рыночное равновесие соответствует оптимальному размеру агломерации, тогда как при промежуточных значениях транспортных расходов социально оптимальной является значительно меньшая агломерация, чем достигаемая в равновесии. Tabuchi & Thisse предложили модель дискретного выбора для описания миграции рабочих и анализа возникающей агломерации.

Наконец, в [26] обобщено моделирование монополистической конкуренции, связанное с CES-функцией полезности, на случай общей функции полезности, получив результаты в терминах коэффициента неприятия риска.

Такой подход объясняет многие наблюдаемые закономерности, среди которых стремление фирм к собственному росту при увеличении рынка CH05, относительно малая продажная цена на больших рынках [35], сосредоточение фирм в окрестности больших рынков [24].

Основываясь на теории Диксита-Стиглица-Кругмана, в работе [17] предложен параметрический метод оценки рыночного потенциала. Из условий общего равновесия на рынках товаров, труда и капитала выводится основное регрессионное уравнение, в котором объясняющими переменными являются торговые балансы между регионами. Видимо, при надлежащем обобщении этот подход может быть применим к оценке инновационной привлекательности регионов.