
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
3.2. Сравнительная оценка инновационной активности регионов
На основе экспертных оценок выделается система показателей, отражающих инновационную активность регионов. Показатели отличаются друг от друга, как по характеристикам измеряемых величин, так и по единицам измерения. Часть этих показателей связаны с затратами на инновации, оставшаяся часть с результатами, полученными за счёт внедрения инноваций. На первом этапе с помощью автоматизированной процедуры множества затратных и результирующих показателей редуцируются до одного-двух с незначительной потерей информации об исходных датах.
На втором этапе по малому количеству модифицированных входных и выходных показателей вычисляется эффективность инноваций. Среди двух регионов с близкими показателями затрат большую эффективность инноваций имеет регион с более высокими результирующими показателями. Если же некоторые регионы имеют близкие результирующие показатели, то более эффективным является тот регион, которых достиг этих результатов при меньших затратах. Указанная идея упорядочения регионов по их эффективности реализуется, если определить эффективность как отношение результирующих показателей к затратным.
Исходные показатели
Для вычисления эффективности использованы следующие показатели.
1) число организаций, выполнявших исследования и разработки;
2) численность персонала, занятого исследованиями и разработками;
3) внутренние затраты на исследования и разработки, тыс.руб.;
4) удельный вес организаций, осуществляющих технологические инновации, %;
5) удельный вес отгруженной инновационной продукции организаций, %;
6) число созданных передовых производственных технологий;
7) число использованных передовых производственных технологий;
8) затраты на технологические инновации, млн.руб.;
9) количество поданных заявок на выдачу патентов на изобретения отечественным заявителям;
10) количество выданных патентов на изобретения отечественным заявителям;
11) затраты на информационные и коммуникационные технологии, млн. руб.;
12) число организаций, использовавших специальные программные средства, всего;
13) число организаций, использовавших специальные программные средства для научных исследований;
14) число организаций, использовавших специальные программные средства для проектирования;
15) число организаций, использовавших специальные программные средства для управления автоматизированным производством или отдельными техническими средствами и технологическими процессами;
16) число организаций, использовавших специальные программные средства для решения организационных, управленческих и экономических задач;
17) число организаций, использовавших специальные программные средства для осуществления электронных расчетов;
18) число организаций, использовавших специальные программные средства для предоставления доступа к базам данных через глобальные информационные сети, включая Интернет;
19) число организаций, использовавших специальные программные средства (редакционно-издательские системы);
20) число организаций, использовавших специальные программные средства (обучающие программы);
21) число организаций, использовавших специальные программные средства (антивирусные программы);
22) число организаций, использовавших специальные программные средства, CRM-Программы;
23) число организаций, использовавших специальные программные средства, ERP-Программы;
24) число организаций, использовавших специальные программные средства, SCM-Программы;
25) число организаций, использовавших прочие программные средства (Источник данных для расчетов).
Автоматизированное уменьшение количества показателей
Уменьшение показателей проводится линейным методом главных компонент. Он реализован в стандартных математических пакетах. Идея метода достаточна проста.
Каждый регион задаётся набором значений выбранных показателей. Этот набор значений определяет точку в многомерном пространстве. Размерность пространства равна количеству показателей. Так как показатели инноваций являются отражением единых глобальных экономических, политических и социальных процессов, то можно ожидать, что заданные точки вкладываются в пространство существенно меньшей размерности с малой ошибкой.
Например, если множество точек плоскости лежит на одной прямой, то это множество одномерно, хотя каждая точка задаётся парой координат. Чтобы продемонстрировать одномерность этого множества точек, следует ввести новую координату, направленную вдоль прямой, на которой эти точки находятся. Тогда каждой точке множества ставится в соответствие новая координата - множество точек одномерно.
В более сложной ситуации множество точек может находиться вблизи некоторой прямой, но не лежать на ней. Тогда, данные апроксимируются прямой, и проектируются на эту прямую. Проекции исходного множества являются одномерными. Прямая, на которой лежат проекции, показывает в каком направлении исходное множество точек вытянуто наиболее сильно.
Выделенное направление называется главной компонентой или главным фактором. Вторая компонента (координатная ось) на плоскости выбирается ортогональной (перпендикулярной) главному направлению. Указанная процедура легко применяется в пространстве произвольной размерности.
Сначала выбирается главное направление, вдоль которого исходное множество наиболее вытянуто. Затем рассматривается подпространство, ортогональное выделенному направлению. Его размерность на единицу меньше размерности исходного пространства. Если исходное пространство было двумерно, то на этом шаге процедура заканчивается, поскольку ортогональное подпространство является прямой (как указано выше), которую и следует выбрать в качестве второй компоненты.
В случае большей размерности исходные точки проектируются на ортогональное подпростанство. Для этих проекций вновь выбирается главное направление, по которому проекции наиболее вытянуты.
Далее опять определяется подпространство, ортогональное выделенному направлению. Его размерность на единицу меньше размерности подпространства, определенному на предыдущем шаге процедуры и на два меньше размерности исходного пространства. Процедура выделения главного направления повторяется до тех пор, пока ортогональное подпространство не окажется одномерным.
Потеря информации
Естественно при проектировании данных на главное направление теряется часть исходной информации. Потерянная информация тем больше, чем дальше от выдленного направления находятся точки.
Если потери при проектировании на главное направление велики, то исходные точки проектируются на плоскость, заданную двумя главными направлениями. Для дальнейшего снижения потерь используются последующие выделенные направления.
Если использовать все выделенные направления, то потери информации не происходит, но и - цель процедуры - количество координат не уменьшилось. Если точки размещать в пространстве наугад, то проектирование на главные направления без значимой потери информации невозможно. Следовательно, количество используемых главных направлений зависит как от вида данных, так и от целей исследования.
Нормировка данных
Координаты исследуемых точек имеют различную природу. Процедура выделения главных компонент использует координаты, как заданные числа, не принимая во внимания единицы измерения данных. Если, например, один из показателей измеряется в тысячах рублей, то изменение единицы измерения на рубли приведет к повышению этого показателя в тысячу раз, тогда как по существу данные не изменились.
Однако увеличение одной из координат всех точек в тысячу раз повысит вытянутость точек вдоль этой координаты. Чтобы процедура выбора главных компонент не зависела от линейных растяжений, предварительно данные нормируют.
Сначала находят минимальное и максимальное значение первой координаты. Из первой координаты каждой точки вычитают найденное минимальное значение, и результат делят на максимальное значение. Затем поступают аналогично с остальными координатами.
В результате каждая модифицированная координата лежит на отрезке [0,1]. Модифицированные указанным образом точки (лежащие в многомерном единичном кубе) подаются на вход процедуре, вычисляющей главные направления.
Выделенные главные компоненты
Исходные данные были разделены на две группы. К затратам отнесены показатели № 1-4,8,9,11-25, к результирующим - № 5,6,7,10. Каждая группа показателей нормируется. К нормированным данным применяется процедура выделения главных компонент.
Оказалось, что главные компоненты обеих групп описывают исходные данные примерно на 75 %. В результате выделения главной компоненты найдено правило (линейное преобразование), которое набору координат исходных точек ставит в соответствие одну новую координату.
Значащие коэффициенты этого преобразования имеют одинаковый знак (как для затратных, так и для результирующих показателей). Для показателей затрат эти коэффициенты отрицательны. Следовательно, повышение произвольного показателя затрат уменьшает результат линейного преобразования, т.е. новую координату. Обратное, разумеется, неверно.
Нельзя утверждать, что если уменьшилась новая координата, то ни один из показателей затрат не уменьшился. Легко понять, что уменьшение одного из показателей при значительном увеличении другого (или других) уменьшит новую координату.
Тем не менее, при вычислениях предполагается, что уменьшение новой координаты свидетельствует об относительном увеличении затрат. Аналогично, коэффициенты линейного преобразования для результирующих координат положительны. Поэтому изменение в большую сторону новой координаты интерпретируется как увеличение результата инноваций.
Эффективность инноваций
На предыдущем шаге каждому региону поставлены в соответствие две координаты. Одна из них описывает затраты, другая - результат инноваций. Таким образом, каждому региону соответствует точка на плоскости.
Все точки сдвинуты (одинаковым образом) так, чтобы, во-первых, их координаты оказались положительными, во-вторых, для каждой точки первая координата (описывающая затраты) была не больше второй, а для одной из точек достигалось равенство. Этим сдвигом устанавливается соотношение между показателем затрат и результирующим показателем. Для каждого региона эффективность определяется как отношение первой координаты ко второй.
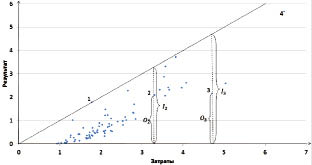
Рис. 10. Эффективность инноваций вычисляются как отношение затратного показателя (вертикальной координаты) к результирующему (горизонтальной)
Примеры вычислений
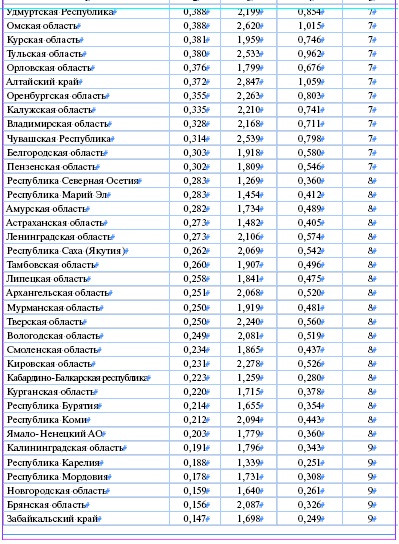
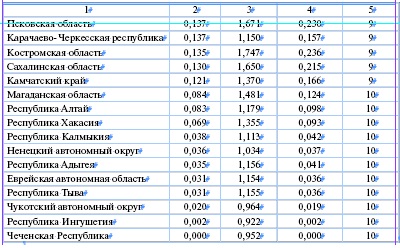
На рис. 10 цифрой 1 обозначена Тюменская область. Обе её координаты I1 и O1 равны 1,765, (табл. 15). Поэтому эффективность инноваций в Тюменской области равна 1. Цифрой 2 на рис. 10 обозначен Красноярский край. Его затратный и результирующий показатели равны I2 = 3,307 и O2 = 2,090. По определению эффективность равна
I2/O2 = 2,090/3,307 = 0,632. Нижнегородская область обозначена на рисунке цифрой 3. Её координаты равны I3 = 4,708 и O3 = 2,158. Поэтому эффективность равна I3/O3 = 2,158/4,708 = 0,458. Полные результаты вычислений эффективности представлены в табл. 15.
Очевидно, как сравнивать эффективность инноваций в регионах, у которых близки затратные или результирующие показатели. Трудности возникают, когда как затратные, так и результирующие показатели существенно различаются.
Например, затраты Хабаровского края I = 2,035, а результат O = 0,817. В Ульяновской области больше как затраты, I = 1,961, так и результат инноваций, O = 0,891. Без специального соглашения об определении эффективности сравнить такие два региона не удается.
Естественно, что чем меньше затраты и чем лучше результаты, тем выше эффективность инноваций. Другими словами, эффективность повышается, чем левее и выше находится точка, соответствующая региону, на рис. 11. Требуется ввести «эталонную» кривую на рисунке, имеющую наивысшую эффективность. Для простоты можно считать, что эффективность лежит между нулем и единицей. Тогда все точки на «эталонной» кривой имеют эффективность, равную единице.
Существуют различные возможности определения «эталонной» кривой. Например, можно определить ее кусочно-линейной, соединяя последовательно самые левые и верхние точки (соответствующие регионам с малыми затратами и высокими результатами), так что выше построенной кривой не находится ни одной точки.
Другие, более тонкие, определения «эталонной» кривой связаны с процедурами интерполяции и построения сплайнов. Сравнение процедур между собой представляет сложную задачу, не являющей целью проекта.
В настоящем исследовании реализована идея линейной «эталонной» кривой, которая соединяет начало координат с такой точкой, при которой выше проведенной прямой не лежит ни одной точки. Даже в этом случае выбор прямой не однозначен, потому что выбор этой прямой связан с выбором начала координат. Фактически необходим экспертный выбор среди малого количества регионов-лидеров, имеющих относительно малый затратный показатель и относительно большой результирующий. После этого эффективность определяется однозначно как отношение затратного показателя к результирующему, как было указано выше.
Обобщение методики
Степень применимости указанной методики зависит от данных. Для используемой выборки данных главная компонента достаточно хорошо описывает исходные данные. Не исключено, что для другой выборки
(с другими показателями, за другой год) использование одной компоненты было бы недостаточно.
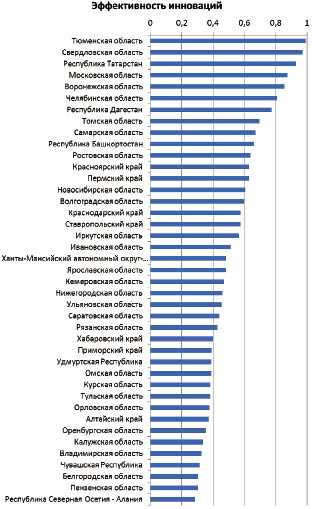
Рис. 11. Ранжирование регионов по индикатору эффективности инноваций
В этом случае применяют группирование исходных показателей с учетом их экономических характеристик с целью получить несколько выборок, у которых главная компонента достаточно полно описывает данные. Тогда эффективность определяют по нескольким рисункам с затратными и результирующими показателями. В конечном итоге, будут определены эффективности различных видов инноваций, которые с некоторыми весами (задаваемыми экспертами) используются при общем определении эффективности.
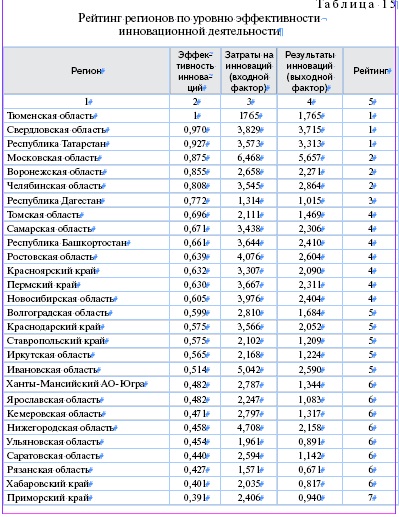
Рейтинг
В соответствии с найденной эффективностью регионы ранжируются, как схематически показано на рис. 11.
Значения эффективности (от нуля до единицы) разделены на десять одинаковых интервалов ((0; 0,1], (0,1; 0,2], ..., (0,9; 1]). Регионам, эффективность которых находится в интервале (0; 0,1] присваивается наиболее низкий рейтинг, равный десяти. Регионам, эффективность которых лежит на следующем интервале присваивается рейтинг 9, и т.д. Тюменской, Свердловской областям и республике Татарстан, имеющим самый высокую эффективность (лежащую на интервале (0,9; 1]), присвоен наивысший рейтинг 1.
