Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Ионные равновесия в водных растворах

Таланов В. М., Житный Г. М.,

1.2.2. Концентрация свободных лигандов и иона-комплексообразователя в растворе комплекса

Реакции комплексообразования в водных растворах, подобно кислотно-основным равновесиям, которые были рассмотрены ранее, по своей сути представляют собой донорно-акцепторные взаимодействия. По этой причине между этими двумя типами равновесий много общего, хотя есть и различия, обусловленные специфическими особенностями каждого из них. Рассмотрим одну из ступеней диссоциации комплекса (например, первую) в растворе

[Ag(NH₃)₂]⁺ D [AgNH₃]⁺ + NH_3.

Здесь донором (D) является комплекс [Ag(NH₃)₂]⁺, акцептором (А) - [AgNH₃]⁺, а переносимой частицей (Х) - молекула NH₃ (лиганд). Константа равновесия для данной ступени диссоциации (первая константа нестойкости) имеет вид:

.

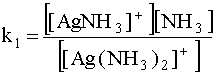Если исходную концентрацию комплекса С_К в первом приближении принять равной его равновесной концентрации, то есть [[Ag(NH₃)₂]⁺] » С_К и выразить отсюда равновесную концентрацию свободных лигандов NH₃ в виде десятичного логарифма этой величины, взятого с обратным знаком (рNH₃), то получим выражение, абсолютно аналогичное выражению рН для растворов слабых кислот (5):

.

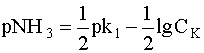или в общем случае

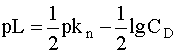(11)

Здесь K_n - константа нестойкости комплекса по n-ой ступени, а C_D - концентрация комплекса, играющего роль донора при диссоциации по той же ступени.

В справочной литературе чаще всего приведены не частные константы нестойкости комплексов, а общие (полные), поэтому целесообразно уравнение (11) преобразовать для случая полной диссоциации комплекса ML_n (без учета зарядов комплексообразователя M, лигандов L и комплексной частицы ML_n в целом). Здесь n – координационное число комплексообразователя М.

Если указанный комплекс подвергается полной диссоциации

ML_n D М + nL

то этому случаю соответствует общая (полная) константа нестойкости К:

.

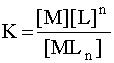Учитывая, что равновесная концентрация иона - комплексообразователя [M] в n раз меньше равновесной концентрации лигандов [L] (что вытекает из уравнения диссоциации), можно записать:

.

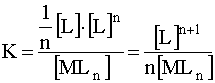Приняв также, что для достаточно устойчивых в водном растворе комплексов равновесная концентрация комплексных частиц [ML_n] приблизительно равна их исходной концентрации С_К, имеем:

.

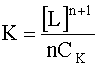Прологарифмируем это выражение и выразим из него рL, введя обозначения рL=-lg[L], pK = -lgK:

.

.

.

.

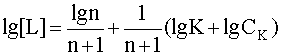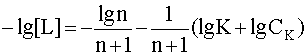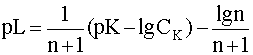(12)

Следует учесть, что для подавляющего большинства одноядерных комплексов координационное число n не превышает восьми. При этом условии последнее слагаемое уравнения (12) можно считать величиной постоянной, приблизительно равной 0,1.

Зная рL, а, следовательно, и равновесную концентрацию лиганда L в растворе, не содержащем ничего, кроме рассматриваемого комплекса, легко найти и равновесную концентрацию свободных ионов комплексообразователя М.

Показатель рL можно рассчитать и тогда, когда известны только равновесные концентрации иона - комплексообразователя [M] и комплексных частиц [ML_n]. Оно выводится аналогично уравнению (8) и в окончательном виде записывается следующим образом:

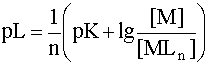(13)

Очевидна полная идентичность уравнений (8) и (13) с той только разницей, что в выражении (13) присутствует сомножитель . Также очевидно и то, что если данное уравнение относится лишь к одной отдельно взятой ступени диссоциации комплекса, то этот сомножитель отсутствует и тогда уравнения (8) и (13), решенные относительно переносимой частицы (протона в кислотно-основных равновесиях и лиганда в реакциях комплексообразования), абсолютно идентичны, что еще раз подчеркивает единую сущность этих двух процессов.