Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
11.2. Текущая и будущая стоимость
При анализе факторов, определяющих эффективность инвестиционных решений, важным является фактор времени. Затраты на доходы, связанные с любой инвестицией, так и иначе расположены во времени. В силу того, что в экономике одновременно существует множество возможностей инвестирования, стоимость затрат и выгод зависит от момента времени, на который они приходятся. Поэтому верная оценка эффективности инвестиций невозможна без правильного соизмерения стоимости этих затрат и доходов во времени.
Пример. Рассмотрим возможность инвестирования, которая при затратах 1 января текущего года в сумме 1 тыс. у.е. принесет 1 января следующего года доход в размере 1,2 тыс. у.е. Предположим, сто риск, инфляция и налогообложение отсутствуют. Выгоден ли такой проект? Если нет никаких альтернативных способов вложения средств, проект, безусловно, выгоден. Но если нет никаких возможность разместить деньги, скажем, на банковском депозите, приносящем годовой доход в размере i процентов, решение будет зависеть от величины i. 1 тыс. у.е. на банковском депозите через год превратиться в 1•х•(1 + i) тыс. у.е. Если это величина будет больше 1,2 тыс. у.е., оцениваемая инвестиция невыгодна, так как банковский депозит приносит большой доход.
Существование альтернативной возможности инвестирования, обеспечивающей доход i процентов на единицу затрат, означает, что сегодняшняя сумма в одну тысячу у.е. через год стоит 1•х•(1 + i) тысяч. Будущей стоимостью сегодняшней суммы денег Сс называется величина, рассчитывается так:
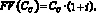(4)
где i – максимально возможный доход в расчете на единицу затрат, который можно получить от альтернативных способов инвестирования за рассматриваемый период времени. Используя тот же принцип, можно рассчитать, сколько стоит некоторая сумма денег, которую мы рассчитываем получить или истратить в будущем, на сегодняшний день. Сегодняшней стоимостью будущего денежного потока Сб называется величина:
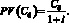
Операцию расчета сегодняшней стоимости будущего денежного потока называют приведением или дисконтированием. Коэффициент, на который необходимо умножить будущий денежный потто, чтобы получить его сегодняшнюю стоимость, называется коэффициентом дисконтирования. Ставка доходности альтернативных возможностей инвестирования, используемая для расчета сегодняшней стоимости, называется ставкой дисконтирования.
Таким образом, оценка эффективности финансовых вложений состоит в сравнении затрат и выгод, приведенных к одному моменту времени. Как правило, затраты и доходы, связанные с инвестиционным проектом, приводит к сегодняшнему моменту времени. В нашем примере, если предположить, что i = 10 %, сегодняшняя стоимость дохода в сумме 1,2 тыс. у.е. равна:
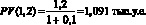
То есть, при данной величине i проект выгоден, так как сегодняшняя стоимость доходов больше сегодняшней стоимости затрат: 1,091 > 1. Оценка эффективности может производиться и по-иному. Назовем доходностью инвестиционного проекта величину, рассчитываемую как:
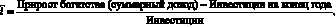(5)
Величина 
характеризует чистые выгоды, подносимые инвестиционном проектом в расчете на 1 у.е. затрат. Доходность банковского депозита в данном примере представляет собой альтернативные издержки инвестирования. Если доходность проекта выше альтернативных издержек: 
– проект выгоден; если 
– невыгоден.
Итак, сегодняшняя стоимость будущего денежного потока в размере Сб у.е., приходящегося на определенный будущий момент времени, – это сумма денег, которую необходимо инвестировать сегодня в наиболее прибыльный из доступных проект, чтобы суммарный доход к рассматриваемому будущему моменту времени составил величину Сб. Сегодняшняя стоимость обычно обозначается в виде функции PV(.), будущая стоимость – FV(.).
Показатели доходности финансовых вложений, как правило, выражают по отношению к определенному временному периоду, например, году. Если ставка годовой доходности инвестиций равна i процентов и доход выплачивается один раз в конце года, то через год на одну у.е, вложений будет получен доход в размере 1 + i у.е. Если средства вкладываются на срок в два года, полученный в конце первого года доход реинвестируется, и, если ставка i останется неизменной, доход на единицу вложений составит (1 + i)•(1 + i) у.е. Таким образом, будущая стоимость сегодняшней суммы денег Сс если годовая доходность альтернативных возможностей инвестирования равна i, через два года составит:
через n лет соответственно:
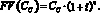(6)
Аналогично, сегодняшняя стоимость денежного потока Сб, приходящегося на момент времени, через, n лет равна:
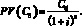(7)
Рассмотрим пример расчета текущей стоимости дохода, получаемого через промежуток времени, не кратный в точности одному году, например, через 7 месяцев, если известно, что альтернативная доходность равна i процентов годовых. Пусть альтернативой является банковский депозит с доходностью i процентов годовых, причем доходы по нему выплачиваются один раз в конце года. Итак, вопрос: какова должна быть доходность инвестиции сроком на 7 месяцев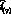 
, чтобы за год с учетом возможности реинвестирования получить 1 + i у.е. в расчете на у.е. затрат,
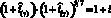
или
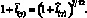
То есть стоимость СС у.е. через 7 месяцев при годовой ставке дисконтирования i составляет:
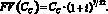
Соответственно, сегодняшняя стоимость суммы дохода Сб, который будет получен через 7 месяцев, равняется:
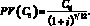
Отметим, что величина 7/12 в нашем примере – есть количество пет в рассматриваемом промежутке времени. То есть формулы (6) и (7) расчета будущей и текущей стоимости справедливы и для дробных величин n, если считать, что выбранная нами альтернатива предусматривает выплату дохода в размере i процентов один раз в год.
Периодичность выплаты доходов по альтернативным инвестиция м при расчете сегодняшней стоимости называется периодом расчета южного процента. Формулы (6) и (7) соответствуют годовому сложному проценту.
Если по некоторому финансовому вложению выплачивается i процентов чистого дохода в год в расчете на единицу инвестиций, а выплаты осуществляются несколько раз в год (например, раз в полугодие или раз в месяц), то фактическая доходность такой инвестиции будет больше i, так как промежуточные выплаты могут быть реинвестированы. Чистый годовой доход в расчете на единицу затрат составит:
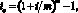(8)
где m – количество выплат в год. Величина ie, рассчитанная по формуле (8), называется эффективной ставкой доходности и зависит от периодичности выплат: чем больше т, тем больше будет ie.
Если в качестве альтернативы рассматриваются инвестиции с доходностью i процентов годовых, причем выплаты осуществляются m раз в год равными долями через равные промежутки времени, формула для расчета будущей (через n лет) стоимости сегодняшнего денежного потока СC примет вид:
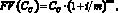(9)
соответственно, сегодняшняя стоимость суммы Сб, которую инвестор планирует получить через n лет, будет равна:
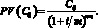(10)
В предельном случае, если период расчета сложного процента считать бесконечно малым (m стремится к бесконечности, то есть процент выплачивается и реинвестируется непрерывно), формулы (9) и (10) принимают вид:
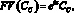(11)
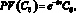(12)
где i – годовая ставка доходности; n – количество лет (в общем случае – дробное число), е – основание натурального логарифмa; е = 2,718272. Результат получен из известной формулы (один из так называемых замечательных пределов):
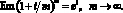
Соответственно, эффективная ставка процента будет равна:
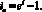(13)
Дисконтирование с непрерывным сложным процентом удобно использовать для небольших промежутков времени, если необходимо сравнить доходность с различной временной структурой выплат.