Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
11.3. Критерии оценки эффективности инвестиций
Рассмотренные принципы соизмерения затрат и доходов во времени позволяют сделать следующий вывод по поводу оценки эффективности инвестиций. Инвестирование выгодно, если суммарная дисконтированная стоимость доходов, обеспечиваемых данным проектом, превышаем суммарную дисконтированную стоимость затрат. Данный критерий ноет название критерия чистой приведенной стоимости (net present value, NPV).
Допустим, имеется инвестиционный проект, предусматривающий чистые денежные потоки с0, c1, c2..., c1, ..., сn в моменты времени 0, 1, 2, ..., t, ..., n соответственно (момент 0 будем считать сегодняшним днем). Чистый денежный поток в момент t определяется как разница между приростом доходов в связи с реализацией проекта и приростом затрат (сt)
Чистой приведенной стоимостью инвестиционного проекта называют суммарную сегодняшнюю стоимость чистых денежных потоков, которые обеспечивает данный проект:
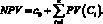(14)
В экономическом смысле чистая приведенная стоимость представляет собой суммарную приведенную стоимость доходов за вычетом суммарной приведенной стоимости затрат. Тем самым критерий NPV инвестиционных решений состоит в сравнении сегодняшней стоимости затрат и доходов; если NPV > 0 – инвестирование выгодно, если NPV < 0 – невыгодно.
Считая, что денежные потоки сt, расположены во времени через равные промежутки, равные одному году (то есть с1; возникает через один год, с2 – через два года, и т.д.), то чистая приведенная стоимость рассчитывается как:
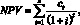(15)
где i – максимальная доходность (процентов в год), обеспечиваемая альтернативными способами вложения средств, причем в формуле (15) мы предполагаем, что i с течением времени будет неизменной. Например, для ранее рассмотренного:
с0 = –1 тыс. у.е.; с1 = 1,2 тыс. у.е.
Если i = 10 %, то:
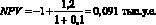
Если длительность промежутков времени между денежными потоками, возникающими в моменты (t – 1) и t (t = 0, .., n), одинакова, но меньше года (например, m, раз в год), чистая приведенная стоимость рассчитывается по формуле:
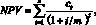(16)
здесь i – годовая доходность альтернативных инвестиций с такой же периодичностью выплат.
В общем случае для произвольной непериодичной последовательности денежных потоков чистая приведенная стоимость рассчитывается по формуле:
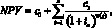(17)
где w(t) – количество лет до момента t; te годовая эффективная доходность альтернативных инвестиций.
Очевидно, что доходность альтернативных инвестиционных решений может меняться с течением времени, поэтому денежные потоки в общем случае должны быть дисконтированы по ставку соответствующей тому моменту времени, в который они возникают, и более точным вариантом формулы (17) будет:
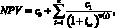(18)
где iet – эффективная доходность альтернативных вложений за врем и от сегодняшнего дня до момента возникновения t-го денежного потока.
Внутренней нормой доходности (internal rate of return, IRR) инвестиции называется такое значение ставки дисконтирования, при кого ром сегодняшняя стоимость затрат равняется сегодняшней стоимости доходов, то есть такое значение i, при котором NPV = 0. В общем случае, внутренняя норма доходности есть решение относительно i уравнения
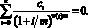(19)
Экономический смысл величины i, полученной из уравнения (19), это такая величина годовой доходности альтернативных способов инвестирования, при условии периодичности выплат т раз в год, при которой чистая приведенная стоимость проекта равна нулю. В дальнейшем под доходностью финансового инструмента будем подразумевать именно величину внутренней нормы доходности, полученную из уравнения (19).
При определении внутренней нормы доходности инвестиций в качестве периода расчета сложного процента берут наименьший период между денежными потоками.
Эффективной внутренней доходностью инвестиции является решение уравнения (16) при m = 1.
Критерий внутренней нормы доходности состоит в сравнении величины IRR и доходности альтернативных инвестиционных решений: проект считается выгодным, если IRR > i.
Все вышесказанное справедливо в случае, что существует полная уверенность в получении будущих доходов на инвестированные средства и полная определенность относительно альтернативных возможностей инвестирования, доходность которых использовалась в качестве ставки дисконтирования. Для оценки сегодняшней стоимости будущих денежных потоков в условиях неопределенности их размеров используется следующее правило: ставка дисконтирования должна соответствовать степени уверенности инвестора в получении будущего дохода, то есть учитывать степень риска, связанного с данной инвестицией. Поэтому в качестве ставки дисконтирования должна использоваться доходность альтернативных инвестиционных решений с такой же или сравнимой степенью риска.
Действительно, для несклонного к риску инвестора две альтернативы по инвестированию средств – при полной определенности и при риске – будут эквивалентны, если ожидаемая доходность рискованной инвестиции превышает доходность безрисковой инвестиции на величину, называемую премией за риск.
Таким образом, если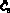 
– случайная величина будущего денежного потока, то его сегодняшняя стоимость равна:
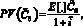(20)
где Е[.] – оператор математического ожидания; – ставка доходности по альтернативным возможностям инвестирования со сравнимой степенью риска, называемая также предполагаемой ставкой доходности для оцениваемой инвестиции.
Известно, что основной проблемой финансовой теории является разработка методов оценки стоимости финансовых активов. Общий принцип оценки состоит в следующем. Стоимость любого актива, не только финансового, но и реального, определяется тем, что владение им дает возможность получения некоторых выгод (доходов) на протяжении определенного промежутка времени. Любой актив обладает стоимостью только потому, что обеспечивает некоторые доходы в будущем. Этот принцип лежит в основе метода расчета истинной (внутренней или инвестиционной) стоимости активов, называемого методом капитализации дохода. Метод состоит в том, что истинная стоимость актива считается равной сегодняшней (приведенной) стоимости денежных потоков, генерируемых данным активом:
Инвестиционная стоимость = суммарная сегодняшняя стоимость будущих денежных потоков.
Более формально: пусть ожидаемые денежные потоки от владения финансовым активом, составляют с1, с2, ..., с1, ..., сn, в периоды времени l, 2, ..., t, ..., n соответственно (положим, что промежутки времени равны между собой, а денежные потоки приходятся на конец каждого периода);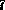 
– предполагаемая доходность оцениваемого актива, то есть максимальная доходность альтернативных инвестиций с такой же степенью риска. Тогда инвестиционная стоимость равняется:
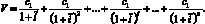(21)
Если Р – текущая рыночная цена рассматриваемого актива, тогда его чистая приведенная стоимость будет равна:
NPV = V – P.
Соответственно, внутренней нормой доходности будет решение относительно i следующего уравнения:
