Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Дискретная оптимизация и моделирование в условиях неопределенности данных
Перепелица В. А., Тебуева Ф. Б.,
1.5. Шкала оценки сложности комбинаторных задач
Напомним, что массовая задача называется полиномиально разрешимой или полиномиальной, если существует такой алгоритм 
ее решения, у которого трудоемкость ограничена сверху полиномом от длины входа 
: 
, где 
– независящая от константа.
Примеры полиномиальных задач:
- назначениях,
- кратчайшем остовном дереве (КСС),
- цепи (пути) между парой вершин.
Неразрешимые задачи – это когда не существует никакого конечного алгоритма, который является разрешаемым для всех индивидуальных задач данной массовой задачи.
Пример Тьюринга:невозможно указать алгоритм, который по произвольной программе определял бы, остановится ли эта программа на произвольно заданном входе или нет.
10-я проблема Гилберта (нахождение целого корня полиномов) также неразрешима, т.е. для нее не существует алгоритма, гарантирующего для всех полиномиальных уравнений нахождение целого корня (Матиясевич Ю.В.). Как отмечено в [27], является неразрешимой так называемая общая диофантова задача: «Задан полином от kпеременных с целыми коэффициентами. Имеется ли у него целый корень?».
Причем, эти и многие другие задачи неразрешимы не только с помощью детерминированных вычислительных устройств, но они неразрешимы и с помощью недетерминированных вычислительных устройств. Они не обладают способностью выполнять параллельно неограниченное количество независимых вычислений (т.е. реализовать одновременно бесконечное число алгоритмов). В [84] устанавливается связь между временной сложностью вычислений на машинах Тьюринга и сложностью схем.
При оценке вычислительной сложности той или другой задачи большую роль играет понятие сводимости одной задачи к другой. Например, задача коммивояжера сводится к задаче о кратчайшем пути на специальном графе. Задача покрытия орграфа произвольным множеством непересекающихся простых контуров сводится к задаче о назначениях и наоборот. Нас интересует здесь и далее сводимость за полиномиальное время.
С. Кук (S. Cook) определил класс NP-задач распознавания свойств следующим образом. Задача 
принадлежит NP, если:
1) решением задачи является один из двух ответов: «да» или «нет»;
2) требуемый ответ может быть получен на недетерминированном вычислительном устройстве за полиномиальное время.
Примеры задач из NP:
- является ли данный граф гамильтоновым;
- содержит ли данный граф остовное дерево
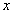степени 
, 
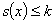; - содержится ли трехмерное сочетание в данном подмножестве декартова произведения трех равномощных непересекающихся множеств? [27] и т.д.
Р. Карп (R. Karp) доказал, что класс NPсодержит широкий подкласс задач, которые полиномиально сводятся друг к другу. Этот подкласс получил название «Класс NP- полных задач». Если задача из этого класса формулируется в оптимизационной постановке, то её принято называть термином «NP-трудная задача».
Наиболее актуальным в наше время вопросом в дискретной математике является: «Верно ли, что NP-полные задачи являются труднорешаемыми?»
Примечание 1.6. Класс NPсодержит 
, т.е 
. Однако не известно, какое из соотношений верно: 
или 
.
Оценивая вычислительную сложность комбинаторных задач, можно использовать следующую шкалу: «полиномиальность» – «NP – полнота (NP- трудность)» – «труднорешаемость» – «неразрешимость».