Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Дискретная оптимизация и моделирование в условиях неопределенности данных

Перепелица В. А., Тебуева Ф. Б.,

2.1. Введение

Для начала вкратце остановимся на предмете «комбинаторный анализ» (КА) или кратко «комбинаторика» (лат. combinare– соединять, сочетать). В задачах КА исследуются дискретные множества, т.е. множества, составленные из отдельных, обособленных элементов. КА – это раздел математики, исследующий приемы, методы нахождения числа всевозможных соединений, сочетаний (комбинаций) при тех или иных определенных условиях из строго заданного конечного множества объектов (букв, цифр, предметов). Чаще всего исследования в традиционной комбинаторике включает два вида действий: отбор определенных подмножеств исходного множества и упорядочение элементов в подмножествах. Эти операции и являются комбинаторными. К настоящему времени можно выделить три основных типа комбинаторных задач.

1. Первый тип составляют задачи существования, когда наличие описанной конфигурации неочевидно и исследование состоит в попытках доказать ее существование. Приведем иллюстрированные примеры для задач I-го типа.

Задача 2.1.Рассматривается группа из любых 6 человек. Доказать, что в этой группе обязательно найдутся трое людей, которые или все знакомы между собой, или все незнакомы.

Задача 2.2.Спрашивается, существует ли в трехмерном пространстве такое расположение  плоскостей, при котором это пространство будет разделено на частей?

Этот же вопрос для плоскости при .

Задача 2.3.Всегда ли можно ограничиться использованием красок только 4-х цветов для того, чтобы всякую географическую карту раскрашивать так, что всякие 2 соседних государства будут окрашены в различные цвета?

К настоящему времени в строгом аналитическом смысле доказано, что пяти цветов достаточно.

Задача 2.4.Рассматривается карта-схема улиц города. Можно ли указать такой маршрут улиц, который по каждой улице проходит 1 раз?

1. Задачи второго типа называют перечислительными. Здесь существование заданных конфигураций известно и требуется либо определить их число либо дать классификацию.

Примеры простейших соотношений для задач этого типа:

а) число всех перестановок  элементов  равно ;

б) число всех сочетаний (без повторений) из  элементов по  элементов равно хорошо известному биномиальному коэффициенту (например, все сочетания элементов  по 2 исчерпываются тремя парами: , , , );

в) число всех сочетаний с повторениями из  элементов по  элементов равно  (например, все сочетания элементов  по 2 с повторениями исчерпываются  парами: , , ,  , , );

г) число всех перестановок без повторений из  элементов по  равно .

Заметим, что число сочетаний с повторениями из  элементов по  есть число решений  уравнения в неотрицательных целых , где  интерпретируется как число появлений элемента  в данном сочетании.

Для решения перечислительных задач достаточно хорошо развит аппарат так называемых производящих функций [79].

2.  Наконец, задачи третьего типа состоят в выделении из всей совокупности решений такого решения, которое обладало бы некоторым свойством в максимальной или минимальной степени. Задачи этого типа обычно называются экстремальными или оптимизационными. Оптимизация над дискретными множествами и является предметом изложения настоящего издания. Приведем примеры экстремальных комбинаторных задач.

Задача 2.5.Пусть имеем  рабочих мест или работ, перенумерованных индексом  и  исполнителей, перенумерованных индексом . Для каждой пары , , , задана величина  – стоимость выполнения -м исполнителем -ой работы. Любое распределение  исполнителей по  рабочим местам определяется перестановкой чисел , где есть номер рабочего места, на которое назначен - й исполнитель. Таким образом, имеем различных вариантов назначений.

Задача о назначенияхсостоит в нахождении такого назначения, или, что то же самое, такой перестановки , при которой суммарная стоимость выполнения всех работ достигает минимума.

Отметим некоторые особенности, которые отличают предмет нашего внимания от классических разделов математики.

1⁰. Комбинаторика – одна из составных частей дискретной математики. Она, в отличие от непрерывной математики, все еще не имеет единой теории. Вследствие этого исследования, ведущиеся в области дискретной оптимизации, отличаются от классических разделов математики обилием частных случаев.

Здесь непрерывно появляются специальные подходы для решения новых постановок задач, которые постоянно выдвигаются практикой.

2⁰. Можно сказать, что поле действия в комбинаторном анализе широкое, а до “переднего края” теории оказывается совсем недалеко. Это замечание в наибольшей степени относится к такому разделу, как экстремальные комбинаторные задачи. Но, несмотря на простоту и наглядность формулировок, большинство из этих задач оказываются очень трудными. Можно назвать комбинаторные задачи, в том числе и экстремальные [17], которые известны с позапрошлого века и до сих пор все еще остаются в строгом смысле нерешенными. Типичный пример – сформулированная выше задача 2.3, которую можно отнести к разряду экстремальных задач в следующей формулировке.

Сначала вводится понятие плоского графа [18], [63], представляющего собой множество из  точек (вершин) на плоскости, некоторые из которых соединены друг с другом попарно непересекающимися кривыми – ребрами. Пример плоского 7-вершинного графа приведен на рис.2.1.

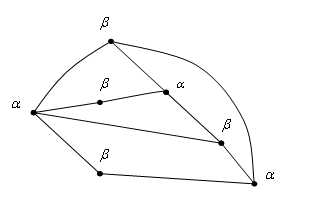
 Рисунок 2.1. Плоский 7-вершинный граф

Будем окрашивать вершины данного графа в цвета . Раскраску вершин называем допустимой, если у каждого ребра концы оказываются окрашенными в различные цвета. На рис.2.1 показана допустимая раскраска всего лишь в два цвета. На рис.2.2 приведен пример 4- вершинного графа, для допустимой раскраски которого по необходимости требуется, очевидно, использовать 4 цвета.

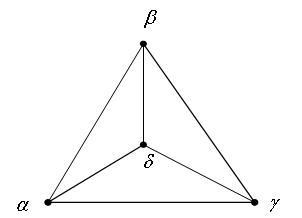
Рисунок 2.2. Полный плоский 4-вершинный граф

 Гипотеза четырех красок:для всякого плоского графа существует допустимая раскраска, использующая не более, чем 4 цвета.

Гипотеза 4-х красок (в терминах задачи 2.1) была известна математикам (Мёбиусу и др.) еще в середине 19-го века. Ею “переболели” очень многие, но до сих пор, с строгом смысле неизвестно, верна ли она, и до сих пор нет алгоритма, который бы с приемлемой трудоемкостью гарантировал допустимую раскраску всякого плоского графа в минимальное число цветов.

3⁰. Комбинаторные идеи и методы всегда были тесно связаны с практическими задачами [82]. В наибольшей степени это положение верно для экстремальных комбинаторных задач. В связи с этим уместно обратить внимание еще на одну особенность, отличающую теорию дискретной (комбинаторной) оптимизации [65] от классической теории вычислительных процессов.

Классическое представление об основном содержании теории вычислительных процессов – это обоснование сходимости предлагаемых алгоритмов. В практическом смысле сходимость означает, что через конечное число шагов или элементарных операций данный алгоритм гарантирует нам решение задачи с заданной точностью. К сожалению, такое классическое представление не соответствует требованиям, которые выдвигает практика решения экстремальных комбинаторных задач. Конечное число операций (для поиска решения) – это качество, оно не является ни необходимым, ни достаточным для эффективного нахождения оптимума, т.е. главной цели, ради которой создавался алгоритм.

Проиллюстрируем последнее утверждение на следующем наглядном примере. Пусть нам нужно найти оптимальное решение задачи о назначении тридцати исполнителей на 30 рабочих мест (см. задачу 2.5). Попытаемся решить эту конкретную задачу с помощью тривиального алгоритма – перебора всех  возможных вариантов назначений. Этот алгоритм для нахождения оптимума, очевидно, требует конечного, но большего, чем  числа операций. После несложных арифметических подсчетов убеждаемся, что даже самая современная ПЭВМ с быстродействием 100 млрд. операций в секунду для поиска оптимального назначения методом перебора потребует более 1 млн. лет непрерывной работы. «К счастью», задача о назначениях является представителем немногочисленного класса полиноминально разрешимых задач; вычислительная сложность этой задачи ограничена сверху полиномом степени  [65].

В силу вышесказанного особого внимания заслуживает вопрос, возникающий в контексте практического использования методов комбинаторной оптимизации в случае, когда реальные исходные данные являются неточными: сколь необходимым является использование алгоритма, гарантирующего нахождение оптимума для всех индивидуальных задач рассматриваемой массовой задачи? Представляется правомерным следующее утверждение: «точные алгоритмы» комбинаторной оптимизации – это «крайний случай» в широком «паретовском спектре» алгоритмов, упорядоченных по убыванию погрешности (в худшем случае) и, соответственно, по возрастанию показателя  вычислительной сложности (также для худшего случая). Иными словами, эффективность алгоритма – это многокритериальная целевая функция и основным является вопрос о выборе алгоритма с наиболее приемлемым (целесообразным) соотношением вычислительной сложности, погрешности и, возможно, других показателей эффективности. В контексте «прикладной комбинаторной оптимизации» актуальную алгоритмическую проблему определяет вопрос построения не одного (допустим точного) алгоритма, а семейства алгоритмов, которые являются несравнимыми по вектору различных показателей их эффективности. Алгоритмы, эффективность которых оценивается двумя критериями («погрешность» – «вычислительная сложность»), принято называть термином «алгоритмы с оценками» [25]. Идея этих алгоритмов адекватна именно условиям неопределенности данных, которым уделяется основное внимание в настоящей книге.