Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ПЛАЗМЕННО-ГИДРОДИНАМИЧЕСКАЯ КОНЦЕПЦИЯ СОСТОЯНИЯ ИОНОВ В РАСТВОРАХ ЭЛЕКТРОЛИТОВ В ОЦЕНКЕ НЕКОТОРЫХ СВОЙСТВ

Балданова Д М, Танганов Б Б,

1.2.2. Вязкость

Проблемы теории вязкости, ее механизма, зависимости от внешних факторов и внутренних характеристик системы, являются до сих пор дискуссионными. Вязкость является структурочувствительным свойством, характеризующим как индивидуальную, так и сложную по составу систему.

Современные теории вязкости зачастую носят эмпирический и полу­эмпирический характер, в которых вязкость рассматривается как функция ряда параметров, как температура, мольный или удельный объем, энергия взаимодействия и др. Как правило, такие модели не претендуют на универсальность и содержат значительное количество эмпирических параметров. Вследствие этого, применимость моделей ограничена набором систем и условий.

Представляет значительный интерес термодинамическая теория скоростей химических реакций, развитая Эйрингом [41]. Механизм течения понимается как последовательность равновесных состояний, относительно определенного положения молекул, которое изменяется при течении. При этом структура жидкости описывается с позиции некоторой доли упорядоченности. В основе этой теории лежит дырочная модель жидкости и представления Я.И. Френкеля [42] о тепловом движении ее молекул, положений равновесия и их скачков из одного положения равновесия в другое. Теории Френкеля и Эйринга выводят и теоретически обосновывают одно и то же уравнение, но по своей сути исходят из различных предположений. Если Френкель жидкость сравнивает с кристаллическим состоянием, то Эйринг в большей степени приписывает жидкости свойства идеального газа. Это приводит как к различным выражениям для предэскпоненциального множителя, так и различному физико-химическому смыс­лу энергии активации вязкого течения. Обе эти теории обладают ограниченностью при описании температурных зависимостей во всем интервале существования жидкостей.

В физико-химических работах, для обработки экспериментальных данных о вязкости растворов электролитов, также используют модифицированное уравнение Эйнштейна [4]

,

где  – «эффективный несжимаемый молярный объем»; C – молярная концентрация электролита.

Уравнение Эйнштейна справедливо для разбавленных суспензий, в которых линии потока вокруг соседних частиц не взаимодействуют между собой, иначе движение ламинарное. Однако в более концентрированных суспензиях взаимодействие линий потока вокруг соседних частиц становится значительным, т.е. появляется турбулентность.

Единственным теоретическим уравнением для описания концентрационной зависимости вязкости водных растворов электролитов является уравнение Фалькенгагена [43]

.

Здесь  – относительная вязкость ( и  – динамическая вязкость раствора и воды при одной и той же температуре); C – молярная концентрация; A – постоянная, является функцией свойств растворителя, подвижностей и зарядов ионов и температуры.

Очевидно, что взаимодействие ион–растворитель должно формализовать сольватные числа ионов и их размеры, это не рассматривается в дан­ной работе.

При увеличении концентрации, когда на вязкость раствора начинают оказывать заметное влияние другие виды взаимодействий в растворе, в частности, взаимодействие ионов растворенного вещества с молекулами растворителя, возникает необходимость вводить в уравнения новые поправ­ки с эмпирическими коэффициентами, зависящими от температуры и концентрации.

Как показано в работе [44] концентрационную зависимость вязкости электролитных растворов часто интерпретируют с позиций полуэмпирического уравнения Джонса-Дола:

,

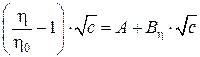где коэффициенты A и  характеризуют взаимодействия ион–ион и ион-растворитель соответственно. Величина коэффициента  и характер его зависимости от температуры и природы электролита для многих веществ получены экспериментально.

Эйчер и Зволинский [41] для описания температурной зависимости вязкости воды и некоторых других жидкостей в интервале от –10 до 150 °С дают следующее выражение, содержащее три эмпирических параметра:

,

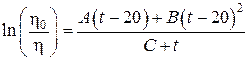где ,  и  – константы, характеризующие данную жидкость.

На основе законов механики Ньютона, а так же Максвелла-Больцмана для распределения частиц по энергиям, Панченковым Г.В. получена более сложная зависимость вязкости от температуры и давления [45]:

,

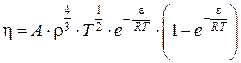где 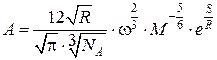; ρ – плотность; ω – собственный объем молекул в расчете на моль; M – молекулярный вес жидкости; S – энтропия образования связи;  – число Авогадро; R – газовая постоянная; T – температура. Очевидно, что существенным недостатком данного метода является отсутствие концентрации электролита C.

Несомненную роль в развитии теории вязкости жидкости установил Бачинский. Он показал линейную зависимость вязкости жидкости от ее удельного объема [46]:

.

Уравнение Бачинского не применимо к ассоциированным жидкостям со сложной молекулярной структурой, но по существу верно обосновывает взаимосвязь вязкости со способностью молекул к свободному перемещению в объеме жидкости.

Балдановым М.М. и Тангановым Б.Б. [47, 48] предложена модель оценки вязкости индивидуальных электролитов:

,

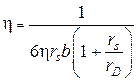отличающаяся от уравнения Стокса множителем 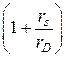, учитывающим колебательный характер процесса и силу сопротивления среды для колеблющейся сферической частицы или иона.

Данная модель действительна только при температуре 298К и внут­ренней энергии реального газа равной , а в случае смесей электролитов не учитывает мольные доли компонентов смесей.

Предложены и другие уравнения для расчета вязкости бинарных систем, которые, как правило, являются менее общими и применимы к оп­ределенному кругу систем со сходными физическими и химическими свойствами.

Таким образом, в теории растворов изучению вязкости уделяется большое внимание, но встречаются противоречивые данные о величинах , определенных для одних и тех же систем. Тем самым, остаются актуальными попытки разработок строгих количественных моделей для исследования вязкости растворов электролитов.