Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Балданова Д М, Танганов Б Б,
2.1. Методы определения ионных радиусов
Ионные радиусы элементов являются одними из ключевых параметров при установлении механизмов элементарных процессов в газовой плазме, физике твердого тела, теории растворов электролитов и т.д.
Существующие системы ионных радиусов в той или иной степени основаны на данных Полинга и Гольдшмидта. По их версии, экспериментально полученные значения межатомных расстояний в ионных кристаллах были разделены на ионные составляющие с помощью различных, по существу, интуитивных предположений.
Так, Полинг исходил из Слетеровских функций распределения с экранированным зарядом ядра и постулирования радиуса иона кислорода 1,4∙10–8 см [52].
Гольдшмидт основывался на примерном равенстве поляризуемости ионов 
и 
, приводящих к 
.
В кристаллах оксидов металлов при этом постулировалось значение радиуса иона кислорода 1,32∙10–8 см [53].
Эти предположения дают близкие значения радиусов по Полингу и Гольдшмидту для однозарядных положительных ионов, за исключением иона 
, и значительные расхождения для двух- и более зарядных.
Из других систем расчета ионных радиусов можно отметить следующие работы. Так, Вебером и Крамером [54] предложены системы орбитальных радиусов, отождествляемых с радиальными расстояниями максимумов электронных плотностей. Их значения найдены на основе решения уравнений Дирака и существенно отличаются от общепринятых значений. Предпочтение орбитальных радиусов перед другими системами не является удачными уже потому, что исходные уравнения оказываются приближенными, а сами радиусы относятся к изолированным ионам в вакууме. Вместе с тем, рассматриваемая система ионных радиусов представляет большой интерес из-за физической логичности следствий, вытекающих при анализе зависимости их изменений от различных факторов: заряда иона, порядкового номера и некоторых других.
Ладд [55], применяя метод Ланде и экспериментальные карты распределения электронной плотности, вычислил набор радиусов ионов при различных координационных числах. Однако использование их не имеет особых преимуществ перед рассмотренными ранее.
Лебедев [56] предлагает систему ионно-атомных радиусов, проявляющихся по линиям связей.
В работах [57, 58] показана возможность использования для решения задачи теоретических оценок ионных радиусов элементов потенциалы ионизаций соответствующих атомов или ионов на основе уравнений электродинамики:
,
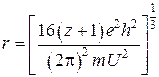где U – потенциальная энергия колебаний, приравненная к сумме энергии атомизации вещества 
и суммы потенциалов ионизации 
, соответствующих образованию «атомного остатка» с зарядом 
, то есть
.
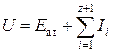Полученное выражение позволяет определять радиусы элементов любых степеней окисления, устойчивых лишь в газовой форме. Но в предлагаемой теории не были учтены эффекты экранирования зарядов. Следовательно, данная методика теоретических оценок радиусов изолированных ионов не может рассматриваться как вполне достоверная.
Рассмотренные выше системы ионных радиусов требуют дальнейшего развития и не имеют пока явных преимуществ перед другими широко используемыми системами, особенно в области термодинамики.
Наряду с кристаллохимическими системами, большой интерес представляют радиусы ионов в растворе. При переходе ионов из кристаллического состояния в раствор, значения радиусов ионов претерпевают определенные изменения, в виде использования различных поправок к кристаллографическим радиусам ионов. Это и понятно, ведь в растворах электролитов ионы сольватированы, т.е. окружены определенным числом ориентированных диполей растворителя, которые прочно удерживаются вблизи иона и участвуют в тепловом движении вместе с ним вплоть до температуры кипения растворителя. В настоящее время способы описания сольватированных комплексов квантово-химическими методами делятся на неэмпирические и полуэмпирические. Те и другие теории являются приближенными, но характер приближений в них различный.
Например, Латимер с сотрудниками использовали поправку +0,085 нм для катионов и +0,01 нм для анионов [59]. Капустинский с сотрудниками вводил поправку для катионов +0,028 нм и для анионов –0,028 нм [60]. Яцимирский использовал поправку для катионов +0,08 и для аионов +0,04 нм. [61]. В работах [62, 63] изложены принципы расчета эффективных радиусов простых катионов и минимальных радиусов анионов:
,
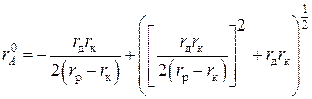где 
– радиус простого катиона; 
– межъядерное расстояние (
– функция структуры); 
– «дебаевский» радиус экранирования (функция постоянной Маделунга, зарядности иона).
Достаточно точная постановка задачи разрешения данных неопределенностей была дана Крестовым Г.А., который утверждал, что «если считать, что заряды иона в кристалле и растворе одинаковы с его зарядом в газообразном состоянии, то наиболее правильно радиус иона в растворе принять равным кристаллохимическому». Следовательно, если считать, что заряды иона в кристалле и в растворе равны некоторому эффективному заряду, отличному от его заряда в газообразном состоянии, то радиусы иона в растворе и в кристалле могут быть различными. Однако учет этих изменений весьма затруднен [64].
Таким образом, приведенный анализ показывает, что ионные радиусы не могут быть найдены экспериментально, а существующие теоретические методы их определения основаны на ряде произвольных допущений, что предопределяет существенную неопределенность при выборе радиусов для конкретных целей.