Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ПЛАЗМЕННО-ГИДРОДИНАМИЧЕСКАЯ КОНЦЕПЦИЯ СОСТОЯНИЯ ИОНОВ В РАСТВОРАХ ЭЛЕКТРОЛИТОВ В ОЦЕНКЕ НЕКОТОРЫХ СВОЙСТВ

Балданова Д М, Танганов Б Б,

2.3. Определение радиусов одноатомных положительных ионов и энергии ионизаций

Нами показана возможность решения задачи определения ионных ради­усов одноатомных положительных ионов с замкнутой электронной оболоч­кой на основе соответствующих потенциалов ионизаций в прибли­же­нии изотропного (или пространственного) осциллятора квантовой
механики.

Так, согласно данной концепции, любой из электронов на внешнем уровне соответствующего иона с замкнутой оболочкой может рассматриваться в приближении изотропного или пространственного осциллятора с потенциальной энергией

,                                          (2.28)

в качестве которой являются приемлемыми первые потенциалы ионизаций этих ионов. Тогда величины r могут рассматриваться как эффективные радиусы или расстояния от этих электронов до ядра. Данная энергия определяется силой

.                                         (2.29)

Весомым аргументом в пользу данного приближения квантовой механики является его эффективность в модели ядерных оболочек, когда движение отдельных нуклонов происходит в сферически симметричном поле совокупности остальных нуклонов у ионов с замкнутой оболочкой в таком же поле ядра и остальных электронов [70].

Что касается ядер, то данное приближение объясняет экспериментально установленные магические числа заполнения 2, 8, 20 и при учете спин-орбитального взаимодействия – чисел заполнения 28, 50, 82, 126 [71].

Использование этого метода для внешних электронов ионов предполагает применение эффективного заряда совокупности остальных электронов, кроме рассматриваемого, в следующем виде:

,

где  – заряд ядра и σ-  константа экранирования, определяемая известными правилами Слейтера-Зинера [71].

Это значение эффективного заряда z, используемое в выражении для определения боровского радиуса иона

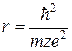                                            (2.30)

как в проблеме Кеплера, приводит уравнение (2.29) к следующему виду

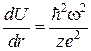.                                         (2.31)

Выражение для полной энергии осциллятора  получается из радиального уравнения Шредингера для функции  [72]:

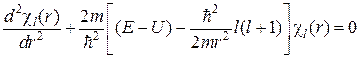,            (2.32)

где U – потенциальная энергия, соответствующая уравнению (2.28); Е – полная энергия любого из внешних электронов ионов; l – орбитальное квантовое число;  – волновая функция, нормируемая условием

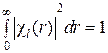,                                      (2.33)

регулярная во всем интервале от . При этом, на пределах интегрирования для  и  она должна обращаться в 

  и  ,

где .

Поэтому, общее решение имеет следующий вид

,                                    (2.34)

где  – параметр, обеспечивающий сшивку. Для этой величины, при , получают уравнение Куммера

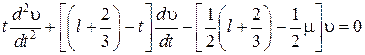.       (2.35)

Здесь . Общее решение этого уравнения известно:

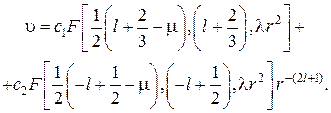                   (2.36)

Поскольку второе слагаемое при  не совместимо с условием нормировки (2.33), принимается  при условии

.                                                (2.37)

Если же , второе слагаемое нормируемо, , но тогда имеет место расходимость интеграла, соответствующего искомой полной энергии, и задача не решается. Таким образом,

, ,

где 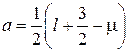,  и .

Вырожденная гипергеометрическая функция  при больших положительных значениях ее аргумента дает экспоненциально затухающее решение при  только в случае если , где  = 0, 1, 2, …- радиальное квантовое число. Раскрывая значение  и , получают уравнение

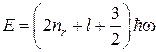,                                    (2.38)

где  – есть полное осцилляторное квантовое число; n_r – радиальное квантовое число. Орбитальное квантовое число l целочисленно, и согласно условию (2.37) , принимает значения 1, 2, 3, …. Отсчет уровней начинается с , тогда  и .

Учитывая особенность решаемой задачи, уравнение (2.38), определяющее полную энергию, можно представить для первого уровня в сле­дую­щем виде:

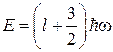.                                     (2.39)

В стандартных изложениях формализма изотропного осциллятора [71], приводящих к полной энергии изотропного осциллятора (2.39), не раскрывается содержание . На самом деле это возможно, если исходить из уравнения Шредингера в форме (2.32), то есть из тех же самых исходных предпосылок.

Обычно сумма второго и третьего слагаемых в скобках в радиальном уравнении Шредингера (2.32) рассматривается как эффективная потенциальная энергия:

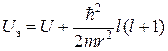.                                (2.40)

Условие экстремума для этой энергии дается выражением

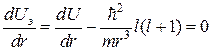.                         (2.41)

Подставляя в данное уравнение (2.41) значение силы  из уравнения (2.31), получаем уравнение, раскрывающее содержание величины :

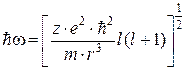.                            (2.42)

Далее, учитывая уравнение (2.42) для  в выражении для полной энергии изотропного осциллятора E (2.39), получаем:

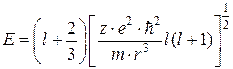.                     (2.43)

Согласно теореме вириала, среднее значение потенциальной энергии осциллятора, равное потенциалу ионизации I, равно половине полной энергии E [72]:

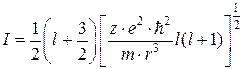.                      (2.44)

Выразив из уравнения (2.44) r, получим выражение для расчета ионных радиусов любых одноатомных положительных ионов:

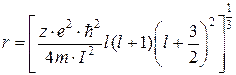, см,                  (2.45)

где I – первый потенциал ионизации соответствующего иона, равный потенциальной энергии любого из внешних электронов.

Для установления значений константы экранирования, входящей в уравнение для определения эффективного заряда , обычно используют аппроксимацию Слейтера [73] для установления вида волновой функции одноэлектронного приближения в методе самосогласованного поля (ССП) Хартри-Фока для многоэлектронных систем.

Конфигурации внешних электронов подразделяют на подсистемы:

 и т.д.

Рассматривается экранирующий эффект на любой из внешних электронов иона, относящийся к одному из приведенных подсистем. При этом:

1) экранирующий эффект любого другого электрона этого же уровня на рассматриваемый составляет 0,35 единиц элементарного заряда за исключением ионов с конфигурацией внешних электронов  (подсисте-
ма 1). Для них эта величина составляет 0,3;

2) вклад в  любого электрона предыдущего уровня составляет 0,85;

3) вклад в  любого электрона более глубоких уровней составляет 1,0 единиц заряда;

4) экранирующий эффект для одного -электрона внешнего уровня со стороны каждого электрона последующего уровня составляет по 1,0 единице заряда, вместо 0,85, как у предыдущих.

Для ионов элементов II периода таблицы Менделеева (,, ,  и т.д.) с конфигурацией  константа экранирования равна  = 0,3, у ионов III периода (, , , , ,  и ) с кон­фи­гу­ра­ци­ей внешних электронов  имеет место

.

Для ионов IV периода с конфигурацией  выполняется  и т.д.

Как показано выше, отсчет уровней для изотропного осциллятора начинается при .

Подставляя это значение  в полученную формулу (1.45) и значения универсальных постоянных e = 4,8∙10^–10 СГС,  СГС,  и  СГС, получаем расчетную формулу:

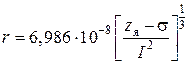, см.

Соответствующие расчеты радиусов ионов  и их сопоставление со значением радиусов ионов в системе Гольдшмидта (Г.), Полинга (П.), Белова-Бокия (Б.Б), Мэлвин-Хьюза (М.Х.) и Ингольда (Ин.) приведены в табл. 2.1-2.7. Потенциалы ионизаций I взяты из [74, 75]. Значения радиусов из различных систем заимствованы из [76].

Таблица 2.1

Радиусы ионов с электронной конфигурацией  ()

Продолжение табл. 2.1

Таблица 2.2

Радиусы ионов с электронной конфигурацией ()

Таблица 2.3

Радиусы ионов с электронной конфигурацией  ()

Таблица 2.4

Радиусы ионов с электронной конфигурацией
 ()

Таблица 2.5

Радиусы ионов с электронной конфигурацией
 ()

Таблица 2.6

Радиусы ионов с электронной конфигурацией
 ()

Продолжение табл. 2.6

Таблица 2.7

Радиусы ионов с электронной конфигурацией  ()