Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Балданова Д М, Танганов Б Б,
2.4. Определение радиусов одноатомных отрицательных ионов
Полученное выше соотношение (2.45) для теоретических оценок радиусов одноатомных положительных ионов в приближении изотропного осциллятора квантовой механики для систем со сферически симметричным распределением вещества и заряда, как ионы с благородно газовыми электронными оболочками, не приемлемо к проблемам образования отрицательных ионов из нейтральных атомов с неспаренными электронами, как атомы галогенов. В таких системах полный спин 
не равен нулю, распределение вещества и заряда не изотропное.
Нам представляется возможным использование для решения данной задачи выражения (2.42) для эффективной потенциальной энергии присоединяемого электрона с нейтральному атому. При этом надо исходить из классического определения энергии сродства к электрону 
в виде [77]:
, (2.46)
где I – полная энергия нейтрального атома, а U – полная энергия отрицательного иона. При образовании отрицательного иона состояние внутренних электронов атома и иона остается практически постоянным. Поэтому, в уравнении (2.46) представим полную энергию нейтрального атома I в виде первого потенциала ионизации нейтрального атома. Полную энергию отрицательного иона U представим в виде потенциальной энергии внешнего электрона, присоединенного к нейтральному атому, с учетом теоремы вириала о среднем значении энергии, как в выражении (2.44), для малых колебаний [72]. Тогда:
,
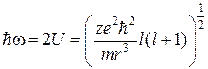или иначе имеет место
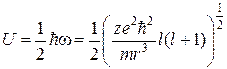. (2.47)
Из уравнения (2.46) следует:
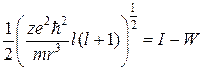. (2.48)
Выразив из уравнения (2.48) r, получим выражение для расчета радиусов одноатомных отрицательных ионов:
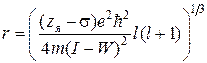. (2.49)
Для примера можно рассмотреть радиусы галогенов. В частности, в процессе
, 
(2.50)
при образовании 
имеет место релятивистский эффект, связанный с взаимодействием спинов присоединяемого электрона и не спаренного электрона атома 
. В этом случае, орбитальный момент и спин всего атома не сохраняются. Остается лишь закон сохранения полного момента 
, являющийся универсальным законом, следующим из изотропии пространства по отношению к замкнутой системе [67].
Подтверждением этому являются термы атомов галогенов 
и их ионов, соответствующие термам благородных газов 
. Очевидно, что полный момент нейтральных атомов галогенов в основном состоянии, при котором присоединяется электрон, равен
.
Поэтому, в формуле (2.49) необходимо использовать вместо орбитального момента 
полный момент 
:
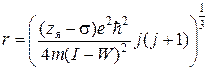. (2.51)
Здесь расчет констант экранирования σ такой же, как и для одноатомных положительных ионов, что дает 
. Далее 
дается в эВ и 1 эВ = 1,6∙10–12 СГС.
Данные расчетов приведены в табл. 2.8.
Таблица 2.8
Радиусы отрицательных ионов атомов галогенов
|
Ионы |
|
|
|
|
|
|
|
3,975 |
4,875 |
6,375 |
6,375 |
6,5 |
|
I, эВ |
17,34 |
13,01 |
11,84 |
10,45 |
9,50 |
|
W, эВ |
3,45 |
3,76 |
3,37 |
3,08 |
2,80 |
|
σ |
5,025 |
11,825 |
28,625 |
40,625 |
78,5 |
|
|
1,30 |
1,80 |
2,08 |
2,29 |
2,46 |
|
|
1,36 |
1,81 |
1,96 |
2,20 |
2,35 |
|
|
1,36 |
1,81 |
1,95 |
2,16 |
2,28 |
|
|
1,33 |
1,81 |
1,96 |
2,20 |
- |
|
|
1,36 |
1,81 |
1,95 |
2,16 |
- |
|
|
1,29 |
1,81 |
1,97 |
2,23 |
- |
Поскольку к нейтральному атому галогена присоединяется 1 электрон, то его заряд, ввиду обменного спин-спинового взаимодействия между внешними электронами отрицательного иона, сообщает всем электронам этого уровня дополнительный эффективный заряд 
= 0,125.
Поэтому экранирующий заряд от любого из внешних электронов увеличивается на эту величину. Тогда, вместо их вклада 0,35 появляется (0,35 + 0,125) = 0,475. Вклады внутренних электронов в экранирующих эффектах остаются теми же самыми, что и для одноатомных положительных ионов – 0,85 и 1,0, кроме аниона 
, для которого 0,475 и 0,85.
Значения экранирующих эффектов Слейтера-Зинера для ионов , , 
, 
и 
, согласно их электронным формулам
равны:
0,475∙7+0,85∙2 = 5,025;
0,475∙7 + 0,85∙8 + 2 = 12,125 = 3,325 + 15,3 + 10 = 11,825;
0,475∙7 + 0,5∙18 + 10 = 29,825 = 3,325 + 15,3 + 10 = 28,625;
0,475∙7 + 0,85∙18 + 18 = 3,325 + 15,3 + 28 = 46,625;
0,475∙7 + 0,85∙18 + 60 = 78,5.
Большая разность между данными рассчитанных по формуле (2.51) и экспериментальными в табл. 2.8, возможно объясняется тем, что у тяжелых атомов в большей степени сказывается эффект спин-орбитального взаимодействия, не формализованный однозначно для тяжелых атомов [78].