Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
3.2. Гидратные числа и массы гидратированных ионов
В качестве гидратного числа принимается количество молей растворителя ![]() , обеспечивающих при заданной температуре Т полную диэлектрическую экранировку заряда иона. При этом полагается, что энергия молекул растворителя на границе гидратного комплекса сопоставима с энергией молекул растворителя, не связанных с ионом, т.е. порядка тепловой
, обеспечивающих при заданной температуре Т полную диэлектрическую экранировку заряда иона. При этом полагается, что энергия молекул растворителя на границе гидратного комплекса сопоставима с энергией молекул растворителя, не связанных с ионом, т.е. порядка тепловой ![]() . Молекула растворителя обладает постоянным дипольным моментом р и дипольным расстоянием R0. Главным фактором в данной ситуации является поведение молекул растворителя во внешнем поле – поле самого иона [81].
. Молекула растворителя обладает постоянным дипольным моментом р и дипольным расстоянием R0. Главным фактором в данной ситуации является поведение молекул растворителя во внешнем поле – поле самого иона [81].
С одной стороны, взаимодействие между ионом заряда ![]() с ns молекулами растворителя является ион-дипольным. При этом потенциалы иона и диполя соответственно равны:
с ns молекулами растворителя является ион-дипольным. При этом потенциалы иона и диполя соответственно равны:
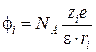 и
и 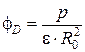 .
.
Их потенциальные же энергии имеют следующий вид:
![]() и
и ![]() ,
,
где m – химический потенциал молекулы растворителя и F – изохорно-изотермический потенциал или свободная энергия Гельмгольца.
С другой стороны, диполь находится в поле точечного заряда с энергией pdE. Тогда дипольный момент молекулы растворителя сохраняется постоянным ![]() . Наблюдается изменение напряженности поля иона с расстоянием. Для такого ион-дипольного взаимодействия справедливо термодинамическое тождество:
. Наблюдается изменение напряженности поля иона с расстоянием. Для такого ион-дипольного взаимодействия справедливо термодинамическое тождество:
![]() . (3.1)
. (3.1)
Значение работы pdE в данном уравнении устанавливается из выражения термодинамики диэлектриков во внешнем поле Ев:
![]() . (3.2)
. (3.2)
Тогда получим выражение
![]() , (3.3)
, (3.3)
Значение SdT определяется выражением:
dU = dF + SdT.
Выразив из этого выражения SdT и подставив в уравнение (3.3), получим выражение вида:
![]() (3.4)
(3.4)
Изменение внутренней энергии в полученном выражении имеет вид:
![]() .
.
Интегрирование уравнения (3.4) приводит к виду:
![]() ,
,
где 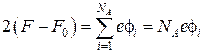 и
и ![]() . Тогда с учетом выражений для потенциалов иона и диполя, а так же их потенциальных энергий, получим следующее уравнение:
. Тогда с учетом выражений для потенциалов иона и диполя, а так же их потенциальных энергий, получим следующее уравнение:
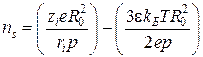 , (3.5)
, (3.5)
где ![]() – заряд иона; R0 – радиус молекулы растворителя;
– заряд иона; R0 – радиус молекулы растворителя; ![]() – радиус иона;
– радиус иона;
р – дипольный момент; е – заряд электрона; e – диэлектрическая постоянная среды; Т – температура; kБ – постоянная Больцмана.
Для некоторых ионов результаты рассчитанных величин гидратных чисел и их сопоставление с литературными данными приведены в табл. 3.1.
Таблица 3.1
Гидратные числа ионов при Т = 298К
|
Ионы |
|
|
ns Р.С. |
ns Э.Э. |
|
|
0,55 |
5,72 |
7,0 |
5,0 |
|
|
1,02 |
3,82 |
3,5 |
4,0 |
|
|
1,26 |
2,92 |
1,9 |
3,0 |
|
|
1,05 |
8,45 |
12,0 |
- |
|
|
0,75 |
12,26 |
13,2 |
13,0 |
|
|
1,41 |
6,01 |
7,7 |
- |
|
|
1,23 |
7,05 |
10,7 |
2,0 |
|
|
0,59 |
24,35 |
- |
21,0 |
|
|
1,81 |
1,69 |
- |
3,0 |
|
|
1,96 |
1,48 |
- |
2,0 |
|
|
2,20 |
1,20 |
- |
1,0 |
|
|
1,30 |
2,774 |
- |
5,0 |
Полученные значения гидратных чисел ![]() по уравнению (3.5) позволяют определять массы гидратированных ионов:
по уравнению (3.5) позволяют определять массы гидратированных ионов:
![]() ,
,
где ![]() – молярная масса растворителя;
– молярная масса растворителя; ![]() – масса иона.
– масса иона.
В случае же бинарных электролитов рассчитываются приведенные массы негидратированных и гидратированных ионов согласно уравнениям: